Бурение грунтовых зондов, установка энергетических колодцев

Согласно справочнику население США распределено по возрас­тным категориям следующим образом (табл. 2.4):

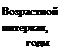
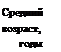
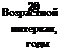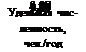Таблица 2.5. Распределение населения США по возрастным категориям

Старше 65

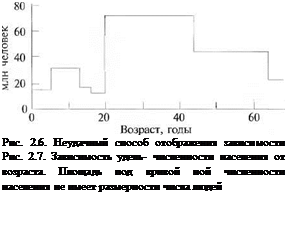
В поисках более удачного и выразительного способа графического представ­ил приведенных выше данных можно построить гистограмму, приведенную •нс 2.6. Однако в силу несопоставимости выбранных временных интервалов ■ограмма не является наглядной. Лучше использовать одинаковый временной эвал, при этом чем он меньше, тем лучше. В пределе наилучшим способом п построение зависимости dN/dA от А, где N — число людей, А — их воз — Для того чтобы сделать это, сформируем другую таблицу на основе данных, іенньїх в табл. 2.4.

1 Данные из последней колонки табл. 2.5 нанесены на рисунке 2.7. Соединим ■ери ментальные точки непрерывной кривой. Площадь под построенной кри — пропорциональна численности населения в стране алогично, для того чтобы распределение по энергиям, например, молекул представленное в графической форме, было достаточно информативным,

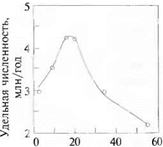целесообразно построить зависимость dN/d W от W или от v (т. е. либо от энер­гии, либо от скорости), а не строить зависимость N от W, как иногда это пы­таются делать.

2.17. МАКСВЕЛЛОВСКОЕ РАСПРЕДЕЛЕНИЕ

Какое число молекул имеет скорости меньшие заданной величи­ны |г-1, если молекулы равномерно распределены по скоростям? Для того чтобы ответить на этот вопрос, давайте вспомним, что в любой момент времени каждая молекула имеет координаты х, у, z и три компоненты скорости: vx, vy, vz. Если речь идет об энергии газа, то точное положение молекул, его составляющих, не имеет значения, но скорости молекул важны. Хотя индивидуальные скорости молекул меняются во времени, в газе с постоянной температурой состояния газа в различные моменты времени статистически эквивалентны. Иными словами, мгновенная картина распределения скоростей в любой момент времени пригод­на для адекватного описания статистического поведения газа.

Давайте графически отобразим скорости молекул в ортогональной системе координат vx, vy и vz — иными словами, в пространстве скоростей. В качестве альтернативы мы можем изобразить импульсы молекул mvx, mvy и mv7 в простран­стве импульсов. Поскольку мы предположили, что молекулы имеют равномер­ное распределение по скоростям (или по импульсам), то пространство скоростей (или импульсов) равномерно заселено. Тогда число молекул, имеющих скорости меньше некоторого значения |п|, пропорционально объему сферы радиусом v (или р) в рассматриваемом пространстве. Отсюда следует, что число молекул со скоростями меньше |п| (или с импульсами меньше |р|) должно быть пропорци­онально v3 (или р3). Тогда число молекул со скоростями в интервале между г и v + do (или импульсами между р и р + dp) должно быть пропорционально

т. е. v2 (или р1). В реальных системах равномерное распределение по скоростям практически исключено. В обычных газах распределение, подтверж — ющееся экспериментальными наблюдениями, таково, что вероятность /найти ■•олекулу, обладающую энергией W, равна:

/ = (82)

В этом случае число молекул со скоростями в интервале между v и v + dv но

— константа, a W= mv2/2.

Это так называемое максвелловское распределение. Очевидно, что

N (полное число молекул) не зависит от температуры. Интегрируя, получаем

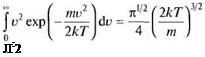(86)

Тогда

рма зависимости dN/dv от v, конечно, меняется с изменением температу­ро изменение можно видеть из рис. 2.8, где Т0 — произвольная реперная ратура. Однако площадь под кривой, будучи мерой полного числа молекул. не зависит от температуры.

Пик зависимости dN/dv равен

ЭТУ _ 2N ( 2т Р Эи е пкТ)

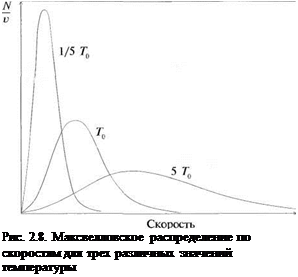и он имеет место при v = (2кТ/тУ! г, что эквивалентно W = кТ.

Когда Т стремится к нулю, ЭТУ/Эитах стремится к бесконечности, что имеет место при v = 0. Распределение принимает вид дельта-функции при Т= 0.

Это означает, что согласно описанной классической теории при температуре, равной абсолютному нулю, все молекулы имеют нулевую скорость и нулевую энергию.

Комментарии запрещены.