Бурение грунтовых зондов, установка энергетических колодцев

В формулы, которые мы получили для удельных теплоемкостей величины у входит величина v, равная числу степеней свободы молекулы, наших рассуждений следует, что v является целым числом и не должна за — от температуры. Что показывают экспериментальные данные? Рассмотрим одноатомные газы. Атомы, из которых они состоят, имеют оступательные степени свободы. В этом случае величина у точно равна 2 3 = 1,667 (см. уравнение (22)). Как следует из данных, приведенных в Г.2, значение у для гелия, аргона и криптона приблизительно (но не точно) ожидаемому значению. Поскольку реальные атомы перечисленных газов рмются точечными объектами, т. е. имеют некоторый объем, то у них дол — зыть спин и по крайней мере одна дополнительная степень свободы долж — ь приписана вращению вокруг собственной оси. В этом случае степеней ты должно быть не меньше четырех и, следовательно, у = 1 + 2/4 = 1,5, что о меньше наблюдаемых значений.

смотрим двухатомную молекулу водорода Н2. Она должна иметь три но — ельные и две вращательные степени свободы. Кроме того, она может совер — вплебательные движения, которые дают еще две степени свободы (одна — » . нетической энергии колебаний, другая — для потенциальной). Таким

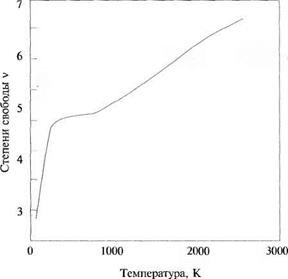
образом, полное число степеней свободы должно быть, по меньшей мере, рав­но семи и соответственно у = 1 + 2/7 = 1,286. При температуре 2300 К у для водорода равна 1,3, что соответствует значению v = 6,67. Как можно видеть из рис. 2.4, только при более высокой температуре число степеней свободы может достигнуть семи. При очень низких температурах значение v стремится к трем и молекулярный водород ведет себя, как точечная одноатомная молекула.

Между этими крайними температурами v плавно меняется, принимая дроб­ные, не целые, значения. Ясно, что молекула может иметь только целое чис­ло степеней свободы, но газ, состоящий из большого количества молекул, характеризуется средним значением v, которое может быть дробным числом. При любой заданной температуре у некоторых молекул возбуждается мень­шее число степеней свободы, в то время как у других — большее. Иными словами, принцип равного распределения энергии между степенями свобо­ды (который требует равного распределения энергии между всеми степеня­ми свободы всех молекул) нарушается. Таким образом, для реальных газов удельные теплоемкости и их отношение у зависят от температуры, хотя и не слишком сильно.

Для оценок можно достаточно предположить, что величины, о которых идет речь, являются константами. При проведении более точных расчетов необходимо обратиться к табличным данным (см., например, перечень экспериментальны. данных по с и у для Н2, 02 и Н20, приведенных в табл. 7.5).

Некоторые общие положения, которые необходимо запомнить, состоят в следующем: переход к более сложным молекулам и более высоким темпе­ратурам приводит к увеличению числа степеней свободы и, следовательно, к большим значениям удельных теплоемкостей и меньшим значениям вели­чины у.

ЭНТРОПИЯ1)

Различные виды энергии можно условно расположить в порядке «ценности». Электрическая энергия должна быть наиболее «ценной» — она ет легко переходить в любой другой вид энергии. То же самое справедли — и для механической энергии, поскольку она может (по крайней мере, тео — "ески) переходить в электрическую энергию и обратно без потерь. Тепло — энергия должна быть расположена в самом низу, так как известно, что она і эжет быть полностью переведена ни в электрическую, ни в механическую ■ энергии (за исключением случая, когда холодильник находится при тем­пе абсолютного нуля). Химическая энергия имеет «ценность» ниже, чем сгрическая энергия, но выше, чем тепловая.

Крэме того, понятно, что чем выше температура, тем выше соответствующая ость» тепловой энергии, поскольку она может быть более эффективно пре — чана в другой вид энергии.

вайте попробуем подвести под эти расплывчатые утверждения количест — ю базу.

смотрим два больших адиабатических тепловых резервуара: один (в даль — ем будем называть его источником) при температуре Тн и другой (тепло — ник) при более низкой температуре Тс. Резервуары связаны тонким ме — еским стержнем, осуществляющим тепловой контакт между ними. Далее южим, что за время эксперимента количество тепла, перешедшего от ника к теплоприемнику, мало по сравнению с количеством тепла, запа-

ред. Этот параграф, касающийся такого важного в термодинамике понятия, каковым энтропия, в книге изложен весьма упрощенно. Для более детального ознакомления рекомендовать соответствующие разделы книги А. К. Кикоина и И. К. Кикоина «Моле — ■ физика». М.: Наука, 1976.

сенного в резервуарах. Из этого предположения следует, что температуры резер­вуаров останутся неизменными.

Предположим также, что стержень, осуществляющий тепловой контакт межд резервуарами, теплоизолирован от внешней среды. Следовательно, количество тепла, потерянного одним резервуаром, точно равно количеству тепла, приобре­тенного другим резервуаром. Тем не менее тепло теряет часть своей «ценности», потому что новая температура меньше прежней[9]). Таким образом, «ценность» тепла теряется при теплопередаче.

Запишем отношение QJ Тдля обоих резервуаров, где Q количество тепла, ко­торым они обменялись. Ясно, что Q/TH< Q/Tc Мы можем рассматривать это отношение как меру «ценности» (или отсутствия «ценности») тепла. Это отно­шение называют энтропией

S^. (68)

Важно понимать, что в рассмотренном примере тепловая энергия сохрани­лась, но ее «ценность» была частично утеряна. Она исчезла из эксперименталь­ной системы не для того, чтобы появиться в другом месте — она была потеря­на в принципе. Закон сохранения энтропии не существует. В любой замкнутой системе энтропия в лучшем случае не меняется, но если она меняется, то только в сторону увеличения[10]). Это утверждение носит название второго закона тер­модинамики.

Нужно понимать, что энтропия является как мерой качества тепловой энер гии, так и мерой беспорядка системы (хаоса). Чем выше температура, связан­ная с количеством тепла Q, тем ниже соответствующая энтропия Q/T. С другой стороны, чем выше температура газа, тем выше беспорядочность движения мо­лекул его составляющих, следовательно, выше энтропия. Чтобы разрешить этот кажущийся парадокс, рассмотрим количество тепла Qm, переданное при темпе­ратуре Tin некоторому объему газа неадиабатическим путем. При этом в газ будет вложена как энергия, так и энтропия. Ясно, что увеличение энергии приведет к росту температуры газа и, в то же время, к увеличению энтропии газа, посколь­ку, хотя энтропия не сохраняется, она согласно второму закону термодинамгаа не может просто исчезнуть. Отсюда следует, что с увеличением температуры газа увеличивается также и его энтропия.

(69)
ь S — энтропия, a AS — ее изменение. Для адиабатического процесса <3(7 = 0. Следовательно,
S = const.	(70)
Для изотермического процесса AS = Q/T, так как Т является константой, тим, что согласно первому закону термодинамики AU= Q — W, но при ерническом процессе AU= 0, следовательно, Q = W. Так как при этом Рі/р2’ то
(71)
Т р2 р2
Для изобарического процесса
(72)
(73)
Йль изохорического процесса
(74)

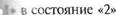
и если с является постоянной величиной, то

Д5 = liCyln^-, (75)

11

Изменение энтропии количества вещества р в киломолях в результате изо­барического фазового перехода

= (76)

где Ql — скрытая теплота фазового перехода (на 1 кмоль), а Т — температура, при которой он происходит.

Все полученные результаты собраны в табл. 2.3.

Комментарии запрещены.