Бурение грунтовых зондов, установка энергетических колодцев

Способность термопары генерировать напряжение при имеющей « разности температур на ее концах можно использовать для создания вой машины, которая преобразует тепловую энергию непосредственно ктрическую. Эффективность такого преобразователя, как и любой тепло — іашиньї, ограничена эффективностью цикла Карно и поэтому может быть — влена в форме

г) = (Тн- Тс) Ц*/Тн, (15)

Рассмотрим простейшую термопару, схема которой показана на рис. 5.8. В электрическое сопротивление R и теплопроводность Л можно выразить следу­ющим образом:

R = 1ЛАЛ °/|) + 1вКАв (Н

А — Ал Ха/1а + Ав A-g/lp 1

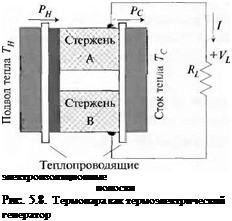где А — площадь поперечного сечения каждого стержня; / — длина каждп стержня; о — удельная электропроводность; X — удельная теплопроводность, метим, что стержни в термопаре расположены параллельно на таком расстоян1 что тепловой поток распределен практически равномерно, а электрический проходит последовательно сначала через один стержень, а затем через друге:

В случае если через термопару протекает электрический ток I, мощное теплового потока, входящего в термопару от источника тепла, как было сна но выше, равна

Рн = А(ТН — Тс) + к1- 1/2RI2. (1

Здесь л представляет собой коэффициент Пельтье, который в данном сл; согласно уравнению (12) пропорционален температуре Та Таким образом.

Рн = А(ТН — Тс) + аТн1- 1/2RP. (I

Ток, протекающий через нагрузку,

а(Тн -7с)

R + Rl

и, следовательно, мощность, выделяющуюся на нагрузке, можно предста как

a 2(Th-Tc)2Rl

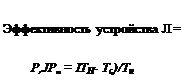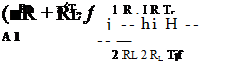(R + Rl)2

Удобно выразить сопротивление нагрузки через сопротивление термопары R. = mR. Тогда, подставив это выражение в формулу (22), получим

где коэффициент добротности термопары Z определяется как

„2

z=

Коэффициент Zимеет размерность обратной температуры, поэтому в системе СИ она измеряется в кельвинах в минус первой степени. В выражении для ц* ■се параметры, за исключением параметра Z, являются внешними. Внутренние характеристики термопары «спрятаны» в Z. Чем больше Z, тем больше эффек­тивность термопары.

Для того чтобы получить высокое значение добротности Z, необходимо вы — К прать материалы для термопары с большим значением коэффициент Зеебека. келательно также, чтобы произведение AR было как можно меньше. Эта цель *">жет быть достигнута путем выбора как соответствующего материала термопар, так и геометрических параметров устройства. Уменьшение длины и увеличение поперечного сечения стержня приведет к снижению электрического сопротивле­ния R, однако теплопроводность Л при этом увеличится. Аналогично увеличение хтины и уменьшение сечения приведет к уменьшению теплопроводности, но сопротивление при этом возрастет. К счастью, можно выбрать геометрические ьраметры, при которых произведение AR минимально. Этот минимум будет четь место, когда геометрия устройства удовлетворяет следующему выраже­нию (см. Приложение)

При этом условии

AR = [(V^)1/2 + (>Уой),/2)2. (26)

Максимальную эффективность термоэлектрического генератора можно полу­чить при правильном выборе значения нагрузки RL, которую мы выразили как R. = mR. Отсюда следует, что необходимо подобрать соответствующее значение т

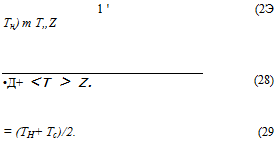Подставив полученное значение т в уравнение для т]*, получим

^ _ (1+ < Т > Z)1/2 -1 _ m -1

Ц (1+ <Т > Z)1/2 +TCITH~ m + Тс Тн ‘ (

Суммируя все вышесказанное, можно прийти к заключению, что сушсств; три различных способа оптимизации эффективности термопары:

1) выбор материалов, обеспечивающих высокое значение добротности Z;

2) выбор геометрических параметров, соответствующих минимальному зна­чению произведения Л/?;

3)

выбор соответствующего сопротивления нагрузки по отношению к внут­реннему сопротивлению устройства, т. е. выбор оптимального значе­ния т.

Максимальное значение ц* будет иметь место при т = Это означает, что сопротивление нагрузки должно быть бесконечно больше сопротивления самой термопары. Другими словами, сопротивление термопары должно быть рай нулю, чего можно добиться, только если в качестве материалов для термопары использовать сверхпроводники. К сожалению, сверхпроводники имеют практи­ческий нулевой коэффициент Зеебека. Следовательно, даже теоретически не­льзя получить эффективность г|* = 1. Даже с помощью новейших разработок области материалов трудно добиться значения добротности Z больше 0,004 К’ Этим обстоятельством объясняется, почему эффективность термопар сущест­венно меньше, чем термомеханических двигателей.

На рис. 5.9 представлена зависимость р* от Тн (при Тс = 300 К) для двух раз­личных значений добротности Z. В каждом из представленных случаев m имеет оптимальное значение. Из этих графиков следует, что эффективность термо­пар, изготовленных по современным технологиям, может составлять (теорети­чески) около 30 % КПД цикла Карно. Современные тепловые электростанции

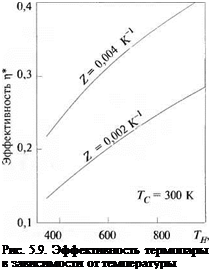имеют КПД на уровне 40 %. Если температура пара на входе в турбину равна Ы2 К, а температура на выходе — 311 К, то КПД пикла Карно составит 61,7 %. Это означает, что реализуется 64 % эффективности цикла Карно, что более чем 2 раза превышает аналогичный показатель в термоэлектрогенераторах.

ДОБРОТНОСТЬ МАТЕРИАЛА

До этого момента мы применяли понятие добротности Z исклю — итедьно к паре материалов, из которых сделана термопара. Удобно использовать іятиє добротности, как характеристику отдельно взятого материала. Это по­лет нам подобрать оптимальную пару материалов для термопары, но сначала походимо расширить определение коэффициента Зеебека.

Измерения и теоретические расчеты показывают, чю коэффициент Зеебека тя любого спая сверхпроводников равен нулю. Это обстоятельство позволяет сти понятие абсолютного коэффициента Зеебека для обычных проводников, предел ив его как значение коэффициента Зеебека для пары материалов, одним з которых является данный материал, а другим — сверхпроводник. Естественно, что значение абсолютного коэффициента Зеебека может быть измерено для температур, при которых наблюдается эффект сверхпроводимости. Так. коэффициент Зеебека для свинца был измерен при температурах в диапазоне от ’.2 до 18 К. При температурах ниже 7,2 К свинец сам становится сверхпро­водником и эффект Зеебека пропадает. Для температур выше 18 К на момент роведения экспериментов не существовало сверхпроводников.

Коэффициент Зеебека для свинца при температурах выше 18 К был рассчн — тан на основе тщательных измерений эффекта Томсона по уравнению (138) (см § 5.14) с использованием уравнения

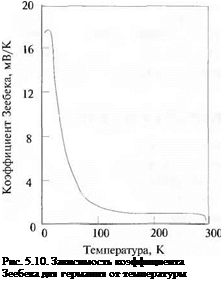
Абсолютный коэффициент Зеебека для других материалов был определен нЯ основе измерений термоЭДС для термопар, в которых одним из материалов яі лялся исследуемый материал, а другим — свинец (см. рис. 5.10).

Теперь, зная коэффициент Зеебека, можно вычислить добротность мате — риала

а[13] 2 <зА I т g

—- = a————- = a — —

Л R I ХА к

В формуле (32) все параметры относятся только к выбранному материал}.

Ясно, что для получения максимальной добротности необходим ма­териал с наиболее высоким значением а и насколько возможно низ­ким значением Х/g. К сожалению, это отношение приблизительно оди­наково для всех металлов. Ниже этот вопрос будет разобран более подробно.

Комментарии запрещены.