Математическая модель воды
Математическая модель воды
Здрасти, с огромным наслаждением читаю статьи на вашем веб-сайте о воде. Я не так давно тоже заинтересовалась исследованием воды и разных фиизческих процессов с ней связанных. Но, потому что я занимаюсь теоретической физикой, меня сначала тревожит вопрос о построении теории воды. Может быть вы располагаете какой-либо информацией о работах в области построения математической модели водянистой воды ? Как я понимаю, в текущее время таковой теории не существует. Есть даже мировоззрение неких учёных, что она вообщем не будет построена.
Мария
Здрасти, Мария.
Спасибо за ваш энтузиазм к нашему веб-сайту.
Существует огромное количество разных теорий и моделей, объясняющих структуру и характеристики воды. Общим у их является представление о водородных связях как основном факторе, определяющем образование структурированных ассоциатов.
1-ая модель воды появилась в 20-х годах прошедшего века. Когда в 20-е годы обусловили структуру льда, оказалось, что молекулы воды в кристаллическом состоянии образуют трёхмерную непрерывную сетку, в которой любая молекула имеет четырёх ближайших соседей, расположенных в вершинах правильного тетраэдра. В 1933 году Дж. Бернал и П. Фаулер представили, что схожая сетка существует и в жидкой воде. Так как вода плотнее льда, они считали, что молекулы в ней размещены не так, как во льду, то есть подобно атомам кремния в минерале тридимите, а так, как атомы кремния в более плотной модификации кремнезёма — кварце. Повышение плотности воды при нагревании от 0 до 4°C разъяснялось присутствием при низкой температуре тридимитовой составляющие. Таким макаром, модель Бернала — Фаулера сохранила элемент двухструктурности, но главное их достижение — мысль непрерывной тетраэдрическои сетки. Тогда появился известный афоризм И. Ленгмюра: „Океан — одна большая молекула“. Излишняя конкретизация модели не прибавила приверженцев теории единой сетки.
Исключительно в 1951 году Дж. Попл сделал модель непрерывной сетки, которая была не так конкретна, как модель Бернала — Фаулера. Попл представлял воду как случайную тетраэдрическую сетку, связи меж молекулами в которой искривлены и имеют различную длину. Модель Попла разъясняет уплотнение воды при плавлении искривлением связей. Когда в 60–70-е годы появились 1-ые определения структуры льдов II и IX, стало ясно, как искривление связей может приводить к уплотнению структуры. Модель Попла не могла разъяснить немонотонность зависимости параметров воды от температуры и давления так отлично, как модели 2-ух состояний. Потому идею 2-ух состояний ещё длительно делили многие учёные.
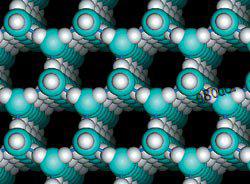
Рис. Модель непрерывной сетки
Во 2-ой половине XX века кроме „континуальных“ моделей (модель Попла), появились две группы „смешанных“ моделей: кластерные и клатратные. В первой группе вода представала в виде кластеров из молекул, связанных водородными связями, которые плавали в море молекул, в таких связях не участвующих. Модели 2-ой группы рассматривали воду как непрерывную сетку (обычно в этом контексте именуемую каркасом) водородных связей, которая содержит пустоты; в них располагаются молекулы, не образующие связей с молекулами каркаса. Несложно было подобрать такие характеристики и концентрации 2-ух микрофаз кластерных моделей или свойства каркаса и степень наполнения его пустот клатратных моделей, чтоб разъяснить все характеристики воды, в том числе и знаменитые аномалии.
Посреди кластерных моделей более броской оказалась модель Г. Немети и Х. Шераги: предложенные ими рисунки, изображающие кластеры связанных молекул, которые плавают в море несвязанных молекул, вошли во множество монографий.
Первую модель клатратного типа в 1946 году предложил О.Я. Самойлов: в воде сохраняется схожая гексагональному льду сетка водородных связей, полости которой отчасти заполнены мономерными молекулами. Л. Полинг в 1959 году сделал другой вариант, предположив, что основой структуры может служить сетка связей, присущая неким кристаллогидратам.
В течение 2-ой половины 60-х годов и начала 70-х наблюдается сближение всех этих взглядов. Появлялись варианты кластерных моделей, в которых в обеих микрофазах молекулы соединены водородными связями. Сторонники клатратных моделей стали допускать образование водородных связей меж пустотными и каркасными молекулами. То есть практически создатели этих моделей рассматривают воду как непрерывную сетку водородных связей. И речь идёт о том, как неоднородна эта сетка (к примеру, по плотности).
Представлениям о воде как о водородно-связанных кластерах, плавающих в море лишённых связей молекул воды, был положен конец в начале 80-х годов, когда Г. Стэнли применил к модели воды теорию перколяции, описывающую фазовые переходы воды. Так появилась смешанная кластерно-фрактальная модель воды.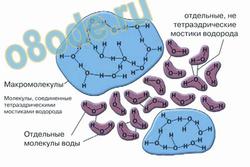
Рис. Современная клатратно-фрактальная модель воды. На рисунке представлены как отдельные кластерно-ассоциативные структуры молекул воды, так и отдельные молекулы воды, не связанные водородными связями.
В 1993 году южноамериканский химик Кен Джордан предложил свои варианты устойчивых “ассоциатов воды”, которые состоят из 6 её молекул [Tsai & Jordan, 1993]. Эти кластеры могут объединяться вместе и со “свободными” молекулами воды за счет экспонированных на их поверхности водородных связей. Увлекательной особенностью этой модели будет то, что из нее автоматом следует, что свободно растущие кристаллы воды, отлично известные нам снежинки, должны владеть 6-лучевой симметрией.
В 2002 году группе д-ра Хэд-Гордона способом рентгеноструктурного анализа при помощи сверхмощного рентгеновского источника Advanced Light Source (ALS) удалось показать, что молекулы воды способны за счет водородных связей создавать структуры — «настоящие кирпичики» воды, представляющие из себя топологические цепочки и кольца из огромного количества молекул воды. Интерпретируя приобретенные экспериментальные данные, исследователи считают их достаточно долгоживущими элементами структуры. В главном же вода – это совокупа хаотичных полимеров и «водяных кристаллов», где количество связанных в водородные связи молекул может достигать сотен и даже тыщ единиц.
«Водяные кристаллы» могут иметь самую разную форму, как пространственную, так и двухмерную (в виде кольцевых структур). В базе же всего лежит тетраэдр. Конкретно такую форму имеет молекула воды. Группируясь, тетраэдры молекул воды образуют разнообразные пространственные и плоскостные структуры. И из всего обилия структур в природе базисной является гексагональная (шестигранная) структура, когда 6 молекул воды (тетраэдров) соединяются воединыжды в кольцо. Таковой тип структуры характерен для льда, снега и талой воды.
Рис. 1. Кристаллическая структура льда
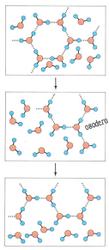Когда лёд плавится, его тетрагональная структура разрушается и появляется смесь полимеров, состоящая из три-, тетра-, пента-, и гексамеров воды и свободных молекул воды. Схематически этот процесс можно представить для себя так.
Рис. справа — Структура водянистой воды. В воде кластеры временами разрушаются и образуются опять. Время перескока составляет 10-12 секунд.
Изучить строение этих образующихся полимеров воды оказалось достаточно трудно, так как вода – смесь разных полимеров, которые находятся в равновесии меж собой. Сталкиваясь вместе, полимеры перебегают один в другой, распадаются и вновь образуются.
Поделить эту смесь на отдельные составляющие тоже фактически нереально. Только в 1993 году группа исследователей из Калифорнийского института (г. Беркли, США) под управлением доктора Р.Дж.Сайкалли расшифровала строение триммера воды, в 1996 г. – тетрамера и пентамера, а потом и гексамера воды. К этому времени уже было установлено, что водянистая вода состоит из полимерных ассоциатов (кластеров), содержащих от 3-х до 6 молекул воды.
Более сложным оказалось строение гексамера. Самая обычная структура – 6 молекул воды в верхушках шестиугольника, – как выяснилось, не настолько высокопрочна, как структура клеточки. Более того, структуры призмы, раскрытой книжки либо лодки тоже оказались наименее устойчивыми. В шестиугольнике может быть только 6 водородных связей, а экспериментальные данные молвят о наличии восьми. Это означает, что четыре молекулы воды связаны перекрёстными водородными связями.
Структуры кластеров воды были найдены и на теоретическом уровне, нынешняя вычислительная техника позволяет это сделать. Более того, конкретно сравнением экспериментально отысканных и рассчитанных характеристик удалось обосновать, что полимеры имеют то строение, которое описано выше.
В 1999 г. Станислав Зенин провёл вместе с Б. Полануэром (на данный момент в США) исследование воды в ГНИИ генетики, которые дали наинтереснейшие результаты. Применив современные способы анализа — рефрактометрию, протонный резонанс и жидкостную хроматографию им удалось найти в воде полиассооциаты воды.
Рис. Вероятные кластеры воды
Объединяясь вместе, кластеры могут создавать более сложные структуры:
Рис. Более сложные ассоциаты кластеров воды
Кластеры, содержащие в своём составе 20 молекулу оказались более размеренными.
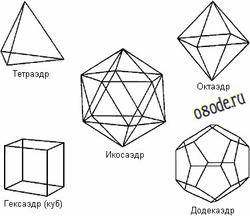Анализируя приобретенные данные С.В. Зенин предложил, что вода представляет собой иерархию правильных больших структур «ассоциатов» (clathrates), в базе которых лежит кристаллоподобный «квант воды», состоящий из 57 ее молекул, которые ведут взаимодействие вместе за счет свободных водородных связей. При всем этом 57 молекул воды (квантов), образуют структуру, напоминающую тетраэдр. Тетраэдр в свою очередь состоит из 4 додекаэдров (правильных 12-гранников). 16 квантов образуют структурный элемент, состоящий из 912 молекул воды. Вода на 80% состоит из таких частей, 15% — кванты-тетраэдры и 3% — традиционные молекулы Н2О. Таким макаром, структура воды связана с так именуемыми платоновыми телами (тетраэдр, додекаэдр), форма которых связана с золотой пропорцией. Ядро кислорода также имеет форму платонова тела (тетраэдра).
Рис. Тетраэдр
Простой ячейкой воды являются тетраэдры, содержащие связанные меж собой водородными связями четыре (обычный тетраэдр) либо 5 молекул Н2О (объемно-центрированный тетраэдр).
При всем этом у каждой из молекул воды в обычных тетраэдрах сохраняется способность создавать водородные связи. За счет их обыкновенные тетраэдры могут объединяться меж собой верхушками, ребрами либо гранями, образуя разные кластеры со сложной структурой, к примеру, в форме додекаэдра.
Рис. Додекаэдр
Таким макаром, в воде появляются бессчетные кластеры, которые несут внутри себя очень огромную энергию и информацию очень высочайшей плотности.
Порядковое число таких структур воды так же высоко, как и порядковое число кристаллов (структура с очень высочайшим упорядочением, которую мы только знаем), поэтому их также именуют «жидкими кристаллами» либо «кристаллической водой».
«Кванты воды» могут вести взаимодействие вместе за счет свободных водородных связей, торчащих наружу из вершин “кванта” своими гранями.
При всем этом может быть образование уже 2-ух типов структур второго порядка. Их взаимодействие вместе приводит к возникновению структур высшего порядка.
Последние состоят из 912 молекул воды, которые по модели Зенина фактически не способны к взаимодействию за счет образования водородных связей.
Этим и разъясняется, к примеру, высочайшая текучесть воды, состоящей из большенных полимеров.
Таким макаром, аква среда представляет собой вроде бы иерархически организованный водянистый кристалл.
Рис. справа — Формирование отдельного кластера воды (компъютерное моделирование)
Необходимо подчеркнуть, что в текущее время есть и другие модели воды, описывающие её аномальные характеристики.
Так, доктор Мартин Чаплин из Английского института (Martin Chaplin Professor of Applied Science Water and Aqueous Systems Research of the London South Bank University) высчитал и представил иную структуру воды, в базе которой лежит икосаэдр.
Рис. Формирование икосаэдра воды
Согласно этой модели вода состоит из 1820 молекул воды — это вдвое больше, чем в модели Зенина. Огромный икосаэдр в свою очередь состоит из 13 более маленьких структурных частей. При этом, так же как и у Зенина, структура огромного ассоциата базируется на более маленьких образованиях.
С почтением,
О. В. Мосин