Характеристики льда и мёрзлых пород
Характеристики льда и мёрзлых пород
НАУЧНЫЙ Журнальчик КРИОСФЕРА ЗЕМЛИ
Как понятно, сегрегационные льды формируются в промерзающих мелкозернистых породах в итоге подтягивания свободной воды к фронту вымерзания. При всем этом образуются слоистые и сетчатые криогенные текстуры.
В практике термических расчетов при оценке теплофизических параметров промерзлых пород с криогенной текстурой характеристики сегрегационного льда обычно задают исходя из характеристик незапятнанного большого льда.
Криосфера Земли, 2008, т. XII, №2, с. 40–46 www.izdatgeo.ru
Характеристики ЛЬДА И Промерзлых ПОРОД ТЕОРЕТИЧЕСКИЕ ОЦЕНКИ Теплопроводимости СЕГРЕГАЦИОННОГО ЛЬДА
Р.И. Гаврильев
Институт мерзлотоведения им. П.И. Мельникова СО РАН, 677010, Якутск, Мерзлотная,36, Наша родина, mpi@ysn.ru
Для оценки коэффициента теплопроводимости сегрегационного льда можно использовать модельное представление пористого льда с цилиндрическими капиллярными (сквозными) и замкнутыми порами повдоль термического потока, также со сферическими воздушными включениями при учете дополнительного конвективного теплопереноса средством диффузии водяного пара в пузырьках. Расчеты можно выполнить на базе теории обобщенной проводимости Максвелла–Рэлея. Показано, что рассчитанные значения коэффициента теплопроводимости сегрегационного льда оказались еще выше, чем экспериментально измеренные, что, может быть, связано с некими методическими упущениями как в расчете, так и в опыте. В предстоящем требуется проведение новых тестов на методической базе, свободной от ограничений по отношению к слоистости испытуемой среды, и воплощение рентгенографических исследовательских работ по уточнению структуры сегрегационного льда.
Сегрегационный и большой льды, пузырьки воздуха, коэффициенты тепло и температуропроводности, большая теплоемкость, диффузия пара
THEORETICAL ESTIMATION OF THERMAL CONDUCTIVITY OF SEGREGATED ICE
R.I. Gavriliev
Melnikov Permafrost Institute SB RAS, 677010, Yakutsk, Merzlotnayastr.,36, Russia, mpi@ysn.ru To estimate the thermal conductivity of segregated ice, a model of porous ice with open and close cylindrical pores along the heat flow and with spherical air bubbles can be used taking into account the additional convective heat transfer by vapour diffusion in air bubbles. The basis (frame) of the model consists of a continuous body of pure hexagonal ice (ice I). Calculations can be based on the Maxwell–Rayleigh theory of generalized conductivity. The calculated thermal conductivities of segregated ice are much higher than the experimental values, probably due to some methodological shortcomings in both the calculation and the experiment. New experiments need to be conducted using a methodology free of limitations on the layered structure of the test medium, and X ray investigations are required to determine more precisely the structure of segregated ice. Segregated and bulk ice, air bubbles, thermal conductivity, thermal diffusivity, volumetric heat capacity, vapour diffusion
ВВЕДЕНИЕ
По экспериментальным данным создателей работ [Гречи щев и др., 2002, 2003], коэффициент теплопровод ности сегрегационного льда, образованного при неспешном замораживании супесчаного грунта в лабораторных критериях, при пористости около 10% составляет порядка 1,1Вт/(м К), что практически вдвое меньше теплопроводимости ( ) незапятнанного льда. Данный факт создатели разъясняют наличием в сегрегационном льду пузырьков воздуха и тем, что во время криогенной передвижения воды раство ренный в ней воздух может создавать самостоя тельный массопоток со своими чертами снутри газированного флюида “вода+воздух”, вы деляясь в виде пузырьков при фазовом переходе воды в лед, фиксируясь в последнем. На этом фоне интересно для сопоставления при вести экспериментальные данные ряда создателей: Н.Н. Зубова [1945], Ю.Л. Назинцева [1964] и В.В. Шулейкина [1968], приобретенные для пористо го большого (громоздкого) льда. Согласно этим данным, теплопроводимость льда при пористости около 20% составляет 1,5–1,8Вт/(м К), в среднем 1,7Вт/(м К), т. е. величина льда за счет пористо сти порядка 20% уменьшилась лишь на 25%. Та ким образом, экспериментальные данные исследо вателей по сегрегационному и объемному льду очень расползаются.
Любопытно было бы проанализировать этот вопрос с единых теоретических позиций посредст вом модельного представления пористого льда с учетом специфичности формирования состава и струк туры льда и строения пор при замерзании воды в мелкозернистом грунте и свободном пространстве.
СВЕДЕНИЯ О СТРУКТУРЕ И СОСТАВЕ СЕГРЕГАЦИОННОГО И Большого ЛЬДА. Черта СТРОЕНИЯ ПОР ВО ЛЬДУ
Для льда понятно девять полиморфных форм [Эйзенберг, Кауцман, 1975]. В обычных природных критериях существует ледI с гексаго нальной кристаллической сингонией – обыденный либо гексагональный лед. Другие восемь форм по лиморфного льда сделаны искусственно при высо ком давлении (выше 2кбар). Они характеризу ются высочайшей плотностью и находятся в метаста бильном состоянии. При переходе к нормальному давлению при низких температурах они превраща ются в обыденный гексагональный лед. Описанное относится к объемному льду.
В грунте связанная вода испытывает огром ное давление поверхностных сил минеральных частиц. Замерзая, она выходит из сферы воздействия поверхностных сил минерального скелета грунта и образует “свободный” лед. При всем этом основная мас са воды кристаллизуется в виде “макроскопичес ких” прослоек льда. Рентгенографические иссле дования, проведенные Т.П. Костецкой и Г.А. Мар тыновым [Основы…, 1959], проявили, что даже при образовании “микроскопичных” кристалликов льда цемента последние выходят из непосредст венного контакта с поверхностью частиц и, следо вательно, также образуют “свободный” лед. Другими словами можно заключить, что сегрегационный и объем ный льды по структуре схожи и относятся ко льдуI с кристаллами гексагональной сингонии (обыденный гексагональный лед).
В промерзлых грунтах структура сегрегацион ного льда плотно сплетена с составом грунта и ус ловиями вымерзания. Согласно исследованиям О.С.Конновой [1957], в тонких шлирах сегрегаци онного льда промерзлого пылеватого суглинка преоб ладают кристаллы пластинчатой формы, а в более массивных ледяных прослойках – в большей степени столбчатые кристаллы. Но независимо от это го незапятнанный лед без пузырьков воздуха имеет посто янный коэффициент теплопроводимости, равный 2,25Вт/(м К) при обычном атмосферном дав лении и температуре 0°С; не считая того, у него не на блюдается анизотропия коэффициента теплопро водности [Вейнберг, 1940]. Это разъясняется тем, что теплопроводимость льда как кристаллического тела определяется фононной передачей термический энергии колеблющейся кристаллической решет кой, независимой от макростроения ледяных крис таллов.
Прослойки сегрегационного льда обычно со держат некое количество минеральных при месей. Но их воздействие на коэффициент тепло проводности льда должно быть некординально. Это можно показать на результатах наших иссле дований (рис. 1), проведенных для влагонасыщен ных промерзлых грунтов в широком спектре изме нений влажности [Гаврильев, 1989]. Как видно на рис. 1, с повышением влажности коэффициент теплопроводимости влагонасыщенных промерзлых
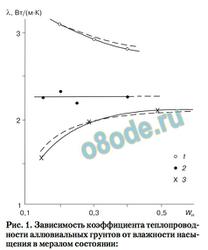Рис.1.Зависимость коэффициента теплопровод ности аллювиальных грунтов от влажности насы щения в промерзлом состоянии:
сплошные кривые – экспериментальные результаты, штри ховые – расчетные; 1 – песок; 2 – супесь, 3 – суглинок.
грунтов стремится к теплопроводимости льда. Ска занное тем паче соблюдается для льда с мине ральными примесями, содержание которых значи тельно меньше, чем количество минерального ске лета во влагонасыщенных грунтах. Во всяком случае воздействие примесей на коэффициент тепло проводности льда полностью можно учитывать на базе теории Максвелла–Рэлея. К примеру, для этой цели можно привести последующее выражение, по строенное по данным рис. 1 [Гаврильев, 2004]:
где Wн 0,15; Wн – влажность полного насыщения грунта. Значения характеристик l1, l2 и l3 даны в таб лице.
Меж влажностью насыщения (Wн) и объем ным содержанием примеси грунта ( ск) существу ет последующая связь: ( )
Главным фактором, от которого зависит ве личина коэффициента теплопроводимости льда, яв ляется его пористость.
Пористость во льду появляется в главном при большой скорости замерзания воды и находится в зависимости от критерий смешивания воды в процессе замерза ния и интенсивности потока воздуха в воде. В ес тественных критериях это может наблюдаться при развитом ветровом смешивании верхнего слоя воды. Для формирования сегрегационного льда плотностью 0,7–0,8г/см3 скорость потока из пу зырьков воздуха, согласно оценкам [Гречищев и др., 2003], может в 3–5раз превосходить скорость крио генного миграционного потока поровой воды.
Поры в объемном льду могут различаться сво ей формой, обоюдным расположением, величиной, наличием либо отсутствием сообщения с верхней и нижней поверхностями ледяного покрова [Савель ев, 1971]. Зависимо от градиентных критерий температуры и давления при образовании льда поры могут иметь самую разную вытянутость повдоль термического потока. С течением времени под действи ем диффузионного переноса пара снутри пор в ре зультате различий упругости пара воды в щелях либо ложбинках и над плоской стеной происхо дит непрерывный процесс преобразования формы пор [Савельев, 1971]. Сначала удлиненные капил лярные поры в узеньких перешейках зарастают, обра зуются замкнутые ячейки, расположенные вереницей в виде цепочек. В конце концов, последние принимают сферическую форму, как более со ответствующую минимуму поверхностной (сво бодной) энергии по условию термодинамического равновесия. Но это процесс долгий и проис прогуливается за геологическое время.
В итоге механических либо тепловых воздействий на ледяной покров во льду образует ся огромное количество маленьких трещинок, придаю щих ему непрозрачный молочный цвет. Но трещинки достаточно стремительно, практически за 10–30ч, исчезают, зарастают, и лед вновь приобретает про зрачность [Савельев, 1971].
При замораживании грунтов в лабораторных критериях в большинстве случаев образуются вытянутые повдоль термического потока (перпендикулярно к плоскости шлира) поры. К примеру, в опытах О.С. Конновой с каолином в шлирах содержалось много цилинд рических пор, вытянутых параллельно кристал лам, часть пор размещалась снутри кристаллов [Савельев, 1971].
В итоге проведенного обзора приходим к последующему выводу относительно структуры и строения сегрегационного льда. Сегрегационный лед состоит из обыденного льдаI, как и в случае большого льда, содержит некое количество минеральных включений и воздушных пор. Форма пор самая разная и с течением времени изменяется, стре мясь, в конце концов, к сферической. Сначала процесса образования льда, в том числе и в лабора торных опытах, поры являются в большей степени цилиндрически капиллярными повдоль термического потока, с течением времени они прерываются в узеньких пе решейках и становятся замкнутыми. Преобразова ния формы и размеров воздушных включений во льду происходят за долгое геологическое вре мя. Трещинные поры, создающие мутность льда, исчезают стремительно.
Для выяснения вопроса о огромных различиях коэффициентов теплопроводимости сегрегационно го и большого льда зависимо от его порис тости проведем модельный опыт с порис тым льдом. За базу модельного представления структуры пористого льда примем сплошное тело из незапятнанного гексагонального льда (остов), содержа щее воздушные поры различной формы, вытяну тости и расположения относительно термического по тока, иногда даже отвлекаясь в какой то степени от реальной картины. При всем этом ставится задачка оцен ки вероятных пределов конфигурации значений коэффициента теплопроводимости пористого льда для сопоставления с приведенными данными по сегре гационному льду.
Разглядим последующие формы пор: сфери ческие, цилиндрические капиллярные (сквозные) и замкнутые, блинчато сплющенные.
Значения характеристик формулы (1) для главных типов грунтов
ТЕОРЕТИЧЕСКИЕ ОЦЕНКИ Теплопроводимости СЕГРЕГАЦИОННОГО ЛЬДА
Сплошные пластинчатые (слоистые) поры из рассмотрения исключаются, потому что при всем этом пропадает устойчивость пористой системы.
СХЕМА РАСЧЕТА
При таком представлении структуры порис того льда совершенно подходит теория Максвелла– Рэлея, на базе которой П. Швердтфегером [Schwerdtfeger, 1963] предложена последующая фор мула для расчета коэффициента теплопроводнос ти пористого льда пл со сферическими воздушны ми порами:
где f= в/ л; в и л – коэффициенты кондуктив ной теплопроводимости воздуха и незапятнанного льда; в – относительное объемное содержание воздуха во льду, равное пористости льда.
В теории Максвелла–Рэлея размеры отдель ных пор не учитываются, оценивается только об щее объемное содержание пор при их схожих размерах и форме.
В случае сложной формы воздушных включе ний (пор) для расчета коэффициента теплопро водности льда можно использовать обобщенную формулу на базе теории Максвелла–Рэлея, предложенную нами ранее для оценки теплопро водности крупнообломочных грунтов [Гаврильев, 1986]:
где Kф – коэффициент формы воздушных пор.
Для общности рассматривается эллипсои далекая форма включений, потому что конфигурацией со дела полуосей эллипсоидов можно полу чить фактически все типы форм воздушных пор. К примеру, для эллипсоидов вращения слоистая пористость обеспечивается при их сплющивании: с/а>0 (с, а – малая и большая полуоси эллипсои дов), когда они преобразуются в пластинчатые прослойки. В случае вытянутых эллипсоидов вращения с радиусом основания с при условии с/а>0 воздушные включения во льду принимают цилиндрическую форму. При всех других значе ниях соотношения с/а отображается эллипсои далекая форма пор с той либо другой степенью вытя нутости либо сплющенности. При с/а=1 воздуш ные включения принимают сферическую форму.
В формуле (3) коэффициент формы включе ний Kф равен K ф=abcC(0), (4) где a, b, c – полуоси эллипсоидов (a>b>c); C(0) – интеграл вида [Овчинников, 1971]
E( , p) – эллиптический интеграл второго рода; = 2 2 arcsin 1 c a – амплитуда интеграла;
Эллиптический интеграл E( , p) протабули рован, а коэффициент формы пор полностью можно отыскать через соотношения их размеров a, b, c.
Впрактических расчетах можно ограничиться бо лее обычным случаем эллипсоидов вращения. Тог да интеграл С(0) выражается через простые функции [Карслоу, Егер, 1964]. Разглядим два примера.
1. Поры имеют форму сплющенного эллип соида вращения (а=b>c). Тогда по фронтам полуосей имеем
2. Поры имеют форму вытянутого эллипсои да вращения (b=c На рис. 2 приведены зависимости вычислен ных по формулам (6)–(9) значений коэффициен тов формы Kф сплющенных и вытянутых эллип соидов вращения от дела малой (с) и боль шой (а) полуосей образующего эллипса по различным фронтам. На рис. 2 видно, что для слоистой пористости (с/а=0) при расположении поровых прослоек поперек потока коэффициент Kф=1 (кривая1), повдоль потока Kф=0 (кривая1 ). В слу чае цилиндрических пор (с/а=0) имеем пер пендикулярно к термическому сгустку Kф=1/2 (кри вая2 ) и параллельно сгустку Kф=0 (кривая2).
При расположении воздушных включений протяженной формы под углом к направлению термического потока коэффициент теплопроводимости льда рассчитывается по формуле
, 2 – вычисленные по формуле (2) при ука занных значениях коэффициента Kф значения ко эффициента теплопроводимости пористого льда при перпендикулярном и параллельном расположении воздушных включений к направлению термического потока.
Коэффициент формы воздушных включений зависимо от соотношения размеров с/а вклю чений меняется в границах от 0 до 1. Для сфери ческих воздушных включений (с/а=1) Kф=0,33.
Если учесть конвективный перенос тепла диффузией водяного пара в воздушных пузырьках под действием градиента температур, то в форму лы (2), (3) заместо кондуктивной теплопроводнос ти воздуха в нужно подставить его эффек тивную теплопроводимость 2, равную [Гаврильев, 1998]
где e0=6,1 102Па – упругость насыщенного пара при 0°С (T0=273K); R=4,6 102Дж/(кг К) – газо вая неизменная водяного пара; T – абсолютная температура,K; L – сокрытая теплота возгонки льда, равная 2,830 106Дж/кг при t=0°С; D – коэффи циент диффузии водяного пара снутри воздушно го пузырька.
Сейчас выясним направленность диффузион ного переноса пара снутри пор и термического потока либо градиента температуры во льду. Понятно, что с увеличением температуры концентрация пара возрастает. Как следует, оба процесса одно направленны, и при учете диффузионного перено са пара в пузырьке воздуха коэффициент тепло проводности воздуха в формулах (2), (3) стано вится только больше, чем в умеренном воздухе (рис.3).
ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
По формуле (3) проведены расчеты коэффи циента теплопроводимости пористого льда при вы деленных выше формах воздушных включений для их разных расположений относительно термического потока: перпендикулярно и параллель но. Для расчетов выбрана температура –5°С, при которой действенный коэффициент теплопровод ности воздуха снутри пор при учете термодиффу зии водяного пара (Dм=0,25см2/с) составляет 0,042Вт/(м К). Необходимо подчеркнуть, что в расчетах цилиндрические замкнутые поры представлены вытянутыми эллипсоидами вращения при с/а= =0,33, а блинчато сплющенные – сплошными эл липсоидами вращения (с/а=0,33).
Результаты расчетов приведены на рис. 4.
Видно, что расхождения значений коэффициента теплопроводимости льда в основном обу словлены ориентировкой пор относительно тепло вого потока, чем различиями в форме пор. Парал лельное термическому сгустку размещение вытяну тых (протяженных) и сплющенных пор всегда обеспечивает огромную величину коэффициента теплопроводимости льда, чем в случае перпенди кулярного их расположения к термическому сгустку.
Осредненная меж ними величина достигается при сферической форме пор. При пористости льда около 20% наибольшие расхождения значений коэффициента теплопроводимости льда для всех рассмотренных форм и направлений воздушных пор не превосходит 30%, а при схожей ориен тировке пор они существенно уменьшаются, на пример, до 10% при параллельном и до 19% при перпендикулярном расположении пор к теплово му сгустку.
Рис.2.Зависимость коэффициента формы Kф воздушных пор в виде сплющенных (1, 1 ) и вытя нутых (2, 2 ) эллипсоидов вращения от парамет ра с/а в различных направлениях:
1, 2 – повдоль оси вращения; 1 , 2 – перпендикулярно к оси вращения.
Рис.3.Температурная зависимость отлично го коэффициента теплопроводимости воздуха внут ри пор.
ТЕОРЕТИЧЕСКИЕ ОЦЕНКИ Теплопроводимости СЕГРЕГАЦИОННОГО ЛЬДА
Отметим, что на рис. 4 даны на теоретическом уровне вероятные спектры конфигураций значений коэф фициента теплопроводимости пористого льда в пре делах пористости до 20%. Выше было показано, что сегрегационному льду, сделанному в лабора торных критериях, более присущи сквозные капил лярные и (с течением времени) замкнутые цилиндричес кие поры, потому изменение теплопроводимости сегрегационного льда зависимо от пористос ти должно происходить согласно кривым1 и 2 на рис. 4. Сегрегационному льду в природных усло виях лучше соответствует кривая4 на рис.4, впро чем, их отличия малозначительные.
На рис. 5 осуществлено сопоставление результа тов расчета пл по формуле (3) при t=–5°C с экс периментальными данными разных создателей для большого и сегрегационного пористого льда. Видно, что модельное представление пористого льда независимо от критерий его образования име ет близкое сходство с экспериментальными дан ными создателей, приобретенными для большого льда. Данные для сегрегационного льда из работ [Гречи щев и др., 2002, 2003] на рис.5 лежат еще ниже, чем все другие. Они оказались даже за преде лами на теоретическом уровне вероятных малых зна чений коэффициента теплопроводимости пористого льда. Непонятно, чем это вызвано.
По видимому, вероятны последующие причи ны этих расхождений:
- –установлена новенькая закономерность, требую щая собственного теоретического осмысления;
- –способ температурной волны в однородном полубесконечном пространстве неприменим для обработки результатов опытов со слоистыми тела ми конечных размеров;
- –при проведении тестов были допу щены погрешности.
Подчеркнем, что изложенное выше является всего только нашей позицией в вопросе о коэффи циенте теплопроводимости сегрегационного льда. В любом случае прояснение в этом вопросе может быть достигнуто только после новых эксперимен тов, может быть, на другой методической базе, на пример, по принципу стационарного термического ре жима, который свободен от каких или ограни чений по отношению к слоистости исследуемой среды.
ВЫВОДЫ
1. Обусловлено модельное представление сег регационного льда для расчета его коэффициента теплопроводимости. В нем базу (остов) модели составляет обыденный гексагональный лед (ледI).
2. Проведен модельный опыт с порис тым льдом при разных формах и ориентации воздушных пор относительно направления теп лового потока, в каком выяснены на теоретическом уровне вероятные спектры конфигурации коэффициента теплопроводимости льда в границах пористости до20%.
3. Показано, что рассчитанные значения ко эффициента теплопроводимости сегрегационного льда оказались еще выше, чем эксперименталь но измеренные [Гречищев и др., 2002, 2003], что, может быть, связано с некими методическими упущениями как в расчете, так и в опыте.
Рис.4.Зависимость коэффициента теплопровод ности пористого льда от ориентировки воздушных пор относительно направления термического потока параллельно (сплошные полосы) и перпендикуляр но (штриховые) при разных формах пор:
1, 6 – цилиндрические капиллярные (сквозные); 3, 5 – ци линдрические замкнутые; 2, 7 – блинчато сплющенные; 4 – сферические.
Рис.5.Теплопроводимость пористого льда: точки – экспериментальные данные: 1 – Ю.Л. Назинцева [1964], 2 – Н.Н. Зубова [1945], 3 – В.В. Шулейкина [1968], 4 – С.Е.Гречищева и др. [2003]; штриховые полосы – расчет ные зависимости для сегрегационного льда при цилиндри ческих капиллярных (I) и замкнутых (II) порах и пористо го льда со сферическими (III) воздушными включениями.
4. Для разрешения появившегося спора о вели чине коэффициента теплопроводимости сегрегаци онного льда требуется, во первых, проведение новых теплофизических тестов на другой методической базе, к примеру, с внедрением способа стационарного термического режима, который свободен от каких или ограничений по отноше нию к слоистости исследуемой среды, во вторых, воплощение рентгенографических исследова ний по уточнению структуры сегрегационного льда.
Работа выполнена при поддержке РФФИ (грант №060596126).
Литература
ВейнбергБ.В. Лед. Характеристики, появление и исчезнове ние льда. М.; Л., Гостехтеоретиздат, 1940, 524с. ГаврильевР.И. Особенности исследования теплофизических параметров грунтов с крупнообломочными включениями // Инж. геология, 1986, №5, с.60–71. ГаврильевР.И. Теплопроводимость вечномерзлых грунтов зависимо от естественной влажности // Инж. физ. журн., 1989, т. 56, №6, с. 995–1001. ГаврильевР.И. Теплофизические характеристики горных пород и напочвенных покровов криолитозоны. Новосибирск, Изд во СО РАН, 1998, 280с. ГаврильевР.И. Теплофизические характеристики компонент природной среды в криолитозоне: Справ. пособие. Новоси ГречищевС.Е., ПавловА.В., ШешинЮ.Б., Гречище ваО.В. Лабораторные исследования физических параметров сегрегационного внутригрунтового льда // Криосфера Зем ли, 2002, т.VI, №1, с. 77–81. ГречищевС.Е., ПавловАрк.В., ШешинЮ.Б., Гречище ваО.В. Зависимость физических параметров сегрегационного внутригрунтового льда от критерий промораживания грун тов // Криосфера Земли, 2003, т.VII, №3, с. 49–54. ЗубовН.Н. Льды Арктики. М., Изд во Главсевморпути, 1945, 360с. КарслоуГ., ЕгерД. Теплопроводимость жестких тел. М., Наука, 1964, 487с. КонноваО.С. Некие результаты исследовательских работ строе ния промерзлых пород // Материалы по лабораторным иссле дованиям промерзлых грунтов, 1957, вып. 3, с. 195–226. НазинцевЮ.Л. Некие данные к расчету термических параметров морского льда // Тр. ААНИИ, 1964, т.267, с.31–47. ОвчинниковИ.К. Теория поля. М., Недра, 1971, 312с. Базы геокриологии (мерзлотоведения). Ч. 1. М., Изд во АН СССР, 1959, 459с. СавельевБ.А. Физика, химия и строение природных льдов и промерзлых горных пород. М., Изд во Моск. ун та, 1971, 507с. ШулейкинВ.В. Физика моря. М., Наука, 1968, 1083с. ЭйзенбергД., КауцманВ. Структура и характеристики воды. Л., Гидрометеоиздат, 1975, 280с. SchwerdtfegerP. The thermal properties of sea ice // J. Glaciology, 1963, vol. 4, No. 36, p. 789–807. Поступила в редакцию