 Рівняння в безрозмірній формі
Рівняння в безрозмірній формі
Виберемо наступні одиниці масштабу: т0 — масштаб маси, однаковий для всіх видів організмів і речовин, to — часу, w0 — кількості теплоти, Т0 — температури, 10 — лінійного розміру 1. Масштаб теп
лоємності с приймемо рівним Co=Wo/m0T0, а коефіцієнта тепловіддачі — 6o=l/toT0l02
Введемо безрозмірні величини:
безрозмірна маса іщ = in,/іп0, (і=1, 2, 3, 4), час t = t/t0, тепло w = w/w0, температура Т = Т/Т0, лінійний розмір 1 = 1/10, теплоємність с = с/с0, площа S = S/lІ, а = а/а0, k = t0/ki (і = ї,2,3,4), kio = t0/k10, kn = t0-T0-ku, ki2 = t0 • m0 • k12, ko =t0 — m0 — k13, kn = t0 • T02 • k14.
Тоді рівняння розвитку мікроорганізмів описане авторами [67, 212] у безрозмірних величинах запишуться у вигляді:
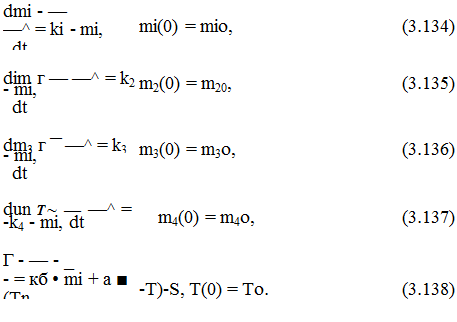 dt
dt
Безрозмірні величини дозволяють побудувати умови подоби процесів. Для цього треба зберегти значення безрозмірних коефіцієнтів, а розмірні можуть мінятися.
Помітимо, що вибір значень масштабів перебуває в нашому розпорядженні. Якщо прийняти, наприклад t0=l (с), 10=1 (т), т0=1 (кг), Т0=1 (1 °С), w0=l (ккал), то масштаби теплоємності с0 і коефіцієнта тепловіддачі б0 також будуть рівними одиниці зі своїми розмірностями. Тоді система рівнянь (3.21)-(3.25) і (3.134)-(3.138) збіжаться не тільки по виду, але і величини масштабів всіх змінних будуть дорівнювати одиниці, це означає, що збіжаться також і чисельні значення рішень.