Бурение грунтовых зондов, установка энергетических колодцев

В залежності від цілей поставлених перед системою управління, зовнішніх діянь, ха­рактеристик об’єкту, принципи автоматичного управління суттєво розрізняються.

Всі автоматичні системи можна умовно розподілити на два великих класи:
— автомати, що виконують як одноразові, так і багаторазові операції;

— автоматичні системи, які в часі змінюють або підтримують які-небудь фізичні вели­чини в управляемому процесі.

Автоматичні системи, в свою чергу, діляться на незамкнуті (розімкнуті) (рис. 1.7) і замкнуті (рис. 1.8).

Якщо джерелом діяння є людина, то така система рахується напівавтоматичною, а якщо джерелом діяння є зміна будь-яких зовнішніх умов (температура, тиск), в яких пра­цює ця система, то така система рахується автоматичною.

Для отримання замкнутої системи управління в розімкнуту систему на виході вклю­чають контрольні прилади, результати вимірювання яких подають на вхід автоматичної системи.

Замкнуті системи існують в техніці у вигляді різних систем автоматичного управлін­ня: автоматичного регулювання, слідкуючих систем, обчислювальних та інше. Вони харак­теризуються тим, що управляюче діяння формується в безпосередній залежності від управляємої величини. Розімкнуті системи здійснюють регулювання по збуренню, а замк­нуті — по відхиленню. Вид управління об’єктом, при якому з необхідною точністю підтриму­ється на протязі часу той чи інший параметр, називається стабілізацією. На рис. 1.9 показана така схема при відсутності неконтролюючих діянь, тобто f « 0.

Рис. 1.9. Схема стабілізації при відсутності діянь

В данній схемі здійснюється управління по збуренню шляхом знаходження функції и = и(д), при якій забезпечується умова у = ует = const, де ует — необхідне значення управляємої величини, що відповідає значенню v.

На рис. 1.10 приведена схема стабілізації при наявності неконтролюючих діянь. В цій схемі здійснюється управління по відхиленню, тобто реалізується замкнута система управління. Управляюче діяння и залежить від різниці між управляемою величиною у і

необхідною v, і направлено на зменшення цієї різниці, тобто и = f(A), де А = у-v.

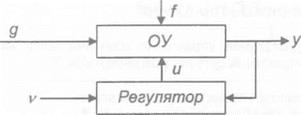Рис. 1.10. Схема стабілізації при наявності діянь

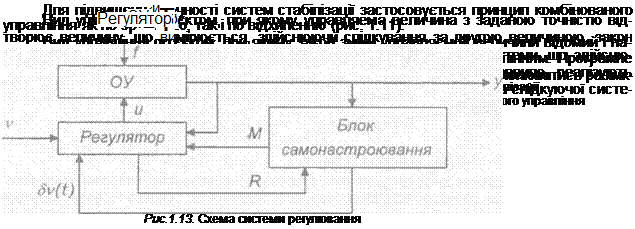Вид управління об’єктом, при якому відбувається забезпечення екстремального зна­чення управляемо! величини або знаходження максимальної швидкодії режиму роботи, називається самонастроюванням (адаптацією). На рис. 1.13 приведена схема системи ре­гулювання по принципу забезпечення максимальної швидкодії. Знаходження цієї умови проходить шляхом подачі пробних задаючих діянь 5v(t). Тут діяння, що змінює парамет­ри регулятора, позначено М, а величина, що дозволяє визначити якість перехідних про­цесів, позначена R. Наявність додаткових управляючих параметрів М і R дозволяє ска­зати, що така система управління вивчає об’єкт і управляє їм, тобто це система подвійно­го управління.

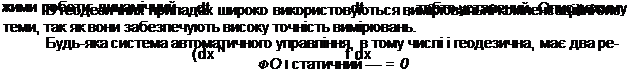
роботи системи виконується за допомогою рівнянь. Математично статичні якості системи відображаються алгебраїчними рівняннями усталеного режиму або рівняннями статики. Графічним відображенням рівнянь статики є статична характеристика. Динамічні ж якості САУ описуються диференціальними (іноді інтегрально-диференціальними) рівняннями. В загальному випадку ці рівняння є нелінійними, однак, при визначених наближеннях, їх можливо замінити лінійними рівняннями, тобто лініаризувати систему диференціальних рівнянь. В лінійних системах перехідні процеси описуються лінійними диференціальними рівняннями з постійними коефіцієнтами і такий метод лінеарізації дозволяє диференціаль­ні рівняння виразити в операторній формі і представити їх у вигляді передаточних функ­цій.

Система автоматичного регулювання певним чином реагує на те чи інше діяння, що подається на її вхід. За звичаєм визначення виду цієї реакції здійснюється шляхом вирі­шення диференціального рівняння, що описує поведінку системи при данній формі збу­рення. Для лініаризованої системи це рівняння може бути представлено у вигляді:

де: xgx = xgx(t) — збуруюче діяння на вході системи;

Хвих = Xeux(t) — реакція на виході;

a0…an, b0…bm — постійні коефіцієнти, що визначаються параметрами системи.

В реальних системах, як правило п>т. В операторній формі рівняння (1.3) можна записати у вигляді:

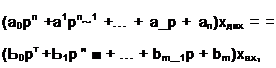(1.4)

де р — символ диференціювання.

Вирішення диференціального рівняння (1.4) звичними методами складно. Викорис­тання операційних методів дає можливість замінити дії, пов’язані з диференціюванням і ін­тегруванням, алгебраїчними діями і виключає необхідність визначення постійних по зада­них початкових умовах.

Найбільш сучасним і ефективним методом такого вирішення є застосування прямого перетворення Лапласа. Перетворення Лапласа здійснює відтворення деякої функції речо­винної змінної f(t), роль якої в нашому випадку відіграє xeux(t), за допомогою функції F(s) комплексної змінної і зворотнього перетворювача, що дозволяє перейти від функції F(s) до функції f(t). Рівняння, що описує пряме перетворення Лапласа має вид

ОС

F(s)= jf(t)e-stdt

о

і символічно представляється виразом

F(s) = L[f(tj[ (1.5)

при цьому F(s) називається зображенням функції f(t), де f(t) — оригінал зображення. Приведене перетворення можливо застосувати тільки для функцій f(t), що задовільня — ють умові f(t) = 0 при t <0.

У відповідності з правилами перетворення Лапласа пряме перетворення для п — ої — похідної від деякої функції часу має вид

де: X(s) — зображення функції x(t)

xQ — початкове значення функції x(t) при t = 0; s — комплексна змінна.

Застосовуючи це правило до диференціального рівняння (1.4), отримаємо

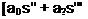+ … + an_1s + an)xeux(s) = (b0sm + as:: ‘ +… +b^s + bm)xgx(s) + xH(s),

Де: xmx(s),.xex(s) — зображення функції xgux(t), xgx(t); xH(s) — функція початкових умов.

При аналізі роботи САУ під впливом зовнішніх діянь звично допускають, що до мо­менту з’явлення діяння система знаходиться в покої або в процесі усталеного руху. При цій умові всі похідні функції початкових умов будуть дорівнювати нулю, відповідно член xH(s) в останньому рівнянні зникне і рівняння прийме вид

(a0sn +a^s"-, +… + an_1s + an)xeux(s)= /

= (b0sm+b1sm~1 + … + bm_1s + bm)xgx(s).

Порівнюючи данне рівняння з раніше отриманим рівнянням в операторному вигляді, бачимо їх ідентичність. Внаслідок цього для збереження найбільш розповсюджених позна­чень замість s будемо в подальшому застосовувати позначення р-s. З рівняння (1.7)

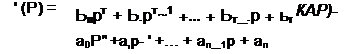маємо

Позначимо

Ь0рт + ьр™-1 +… + Ьт_,р + Ьт = а0рп +а, р — • + … + ап_1р + ап

Тоді отримаємо

XeJp) = W(p)Xgx(p). (1.10)

Величина W(p) носить назву передаточної функції системи. Ця функція характери­зує властивості аналізуючої системи і тому може бути названа власною передаточною функцією.

Аналогічна функція, що визначає не тільки властивості системи, а і характер збурен­ня, носить назву узагальненої передаточної функції. Таким чином, передаточною функці­єю ланки, ділянки ланцюга ланок або всієї системи називається відношення перетворення Лапласа для величини на виході до перетворення Лапласа для діяння на вході при нульо­вих початкових умовах, тобто

Комментарии запрещены.