Бурение грунтовых зондов, установка энергетических колодцев

Процесс разрушения горных пород обычно моделируется изуче­нием явлений, происходящих при вдавливании резца в породу, часто для упрощения поставленных задач резец заменяется пуансоном с уче­том того, что резец не имеет острой режущей кромки и всегда затуплен.

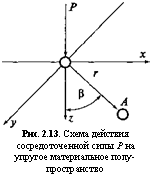
Рис. 2.13. Схема действия сосредоточенной силы Р на упругое материальное полу­пространство

Породы забоя скважины находятся в ус­ловиях сложного напряженного сжатия под Действием горного и пластового давления, а также гидростатического и гидродинамиче­ского давления промывочной жидкости. Взаи­модействия резца-пуансона с горной породой рассмотрим с позиций теории упругости.

Задача Буссинеска

Буссинеск рассмотрел действие сосредо­точенной силы Р на упругое материальное полупространство (рис. 2.13).

В точке А напряженное состояние опре­деляется следующими компонентами напря­жений:

3 Р з„

Ог= — — С083 р,

2 кг2

(2.57)

сх = ^ (1 + 2ц)( сое р — -—-— .,

2 кг2 ‘ н 1 + С08Р]’

1 Р

1

(1-2 ц)

1 + сое р

2 7гг2

Зсов р вт2 р

где — вертикальное напряжение; Р — сила; г—расстояние между точкой контакта силы Р и точкой А:

При (3 = 0

1 Р

®<=4-т; (2-59)

2 л:/-2

= (2’60)

Все напряжения на оси симметрии являются сжимающими. На по­верхности образца при р = п/2

(2.61)

ог = 0,

2 кг2 Р

сх= -(1 — 2ц) ау = (1 — 2ц)

2кг2

Если ах = ау, то это указывает на то, что имеет место деформация чистого сдвига.

При г -> 0 ах -»оо. Следовательно, сжимающие напряжения на по­верхности образца из вышеприведенных формул определить нельзя. Используя принцип Сен-Венана, сосредоточенную силу Рх можно за­менить эквивалентной ей по величине равномерно распределенной нагрузке Р’ по кругу радиусом а. Тогда нормальные напряжения на любом расстоянии от поверхности определяются следующей формулой:

(2.62)

1-

о = Р’

1+1*

При г = 0 аг = Р при аг->0.

Упругая деформация на поверхности круга в этом случае распре­деляется неравномерно. В центре круга:

2(1 — ц2)Р’а

Оп= ‘

(2.63)

на контуре:

(2.64)

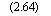1,27(1 — і2)Р’а

а =

Под жестким пуансоном диаметром 2а, как это следует из задачи Буссинеска, давление под ним распределено неравномерно:

2жа^а2 — х2

В центре пуансона (х = 0) давление равно:

(2.66)

Р

^ 2 па2

На контуре х = а Р—>°°.

Касательные напряжения, возникающие в образце под пуансоном и имеющие одни и те же численные значения, распределяются на изохромах (окружностях), проходящих через края пуансона (рис. 2.14).

Анализ приведенных формул показывает, что при г>0 все глав­ные нормальные напряжения убывают, при этом ог снижаются мед­леннее, чем ах и су. Касательные напряжения с глубиной увеличива­ются и при

(2.67)

достигают максимального значения, а затем уменьшаются.

Глубину Zщl называют критической, касательные напряжения в этой точке достигают т0тах = 0,33Р для коэффициента Пуассона р. = 0,3. На этой глубине часто возникают трещины, которые инициируют скол породы. Диаметр сколотой лунки существенно больше диаметра пуан­сона.

Под пуансоном формируется ядро уплотненной породы диамет­ром, равным диаметру рабочей части пуансона. При поступательном движении неуплотненная порода сдвигается по поверхности ядра.

! При достижении предельного значения касательные напряжения распространяются по плоскости, расположенной под углом 45° к оси пуансона. Так как в зоне ядра касательные напряжения достигают предельных значений, то за границами сферы ядра образуются тре­щины. По мере роста касательных напряжений пластические сдвиги

Р

V- Рис. 2.14. Распределение касательных напряжений в образце под пуансоном

породы происходят и по плоскостям, лежащим под углом более 45°, поэтому скол породы распространяется до тех пор, пока не выйдет на поверхность тела за пределы поля, ограниченного торцом пуансона. Скол породы сопровождается выбросом ее части наружу, в то время как часть породы оказывается зажатой между пуансоном и дном лунки.

При взаимодействии резца с породой возникает напряженное со­стояние, близкое к всестороннему. В этом случае сопротивление поро­ды внедрению резца может бьггь достаточно высоким, поэтому разру­шение породы происходит при больших контактных давлениях, в сред­нем в 10—12 раз превышающих предел прочности при одноосном сжатии.

Теоретически установлена следующая зависимость между прочно­стью породы при всестороннем сжатии о3 и прочностью ее при одно­осном сжатии о •

(2.68)

о3 = (2л+ 1)ос:

Таким образом, под прочностью горных пород при бурении по­нимается сопротивление породы внедрению в нее другого более твер­дого тела — резца, упругой деформацией которого можно пренебречь.

Работу лопастных долот можно моделировать внедрением длинно­го пуансона в горную породу (ширина 2а) под действием равномерно распределенной нагрузки:

Напряжение в точке А (рис. 2.15)

SHAPE \* MERGEFORMAT

—

(2.69)

4

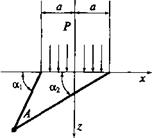
у | а2 — а, + j (sin 2а2 — sin 2cq) }■,

~ < а2 — а[ — j (sin 2а2 — sin 2а

На поверхности образца а, = л; а2 = 0; оу = Р и az = — P.

= sin 2а; sin 2а2 = — sin 2а.

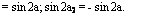
оу = — у (л — 2а — sin 2а), р az = — — (ж — 2а + sin 2а).

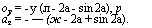
Рис. 2.15. Схема внедрения пуансона шириной 2а в гор­ную породу под действием

Теперь формулы (2.69) принимают вид

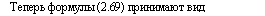
(2.70)

Касательные напряжения описывается зависимостью: о, — а, р х = —^— = у вт2а. (2.71) При г=0 а = 0 и х = 0; а = 45° х0пих = Р/ж. Максимальные касательные напряже-

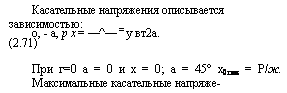Введем новые величины: а, = а; а2 = л — а; а2 — а! = л = 2а, • sin 2а, =

равномерно распределенной ния возникают на глубине Ь = а. Сводные нагрузки р данные о местоположении критической

Таблица 2.13. Местоположение критической точки Форма пуансона Положение критической точки Ь на глубине Численные значения Т0|гах Круглый плоский с радиусом а 0,637а 0,ЗЗ. Р (Р— среднее) Цилиндр с шириной полоски 0,78 а 2 Р/ка контакта 2а Длинная полоска шириной 2 а а P/к (Р— равномерно распределенное давление)

точки b и численного значения т0шах для рассмотренных задач приве­дены в табл. 2.13.

Следует отметить, что в случае наличия сил трения по поверхно­сти штампа о породу при его перемещении критическая точка b сме­щается в направлении перемещения пуансона.

Задача Буссинеска позволяет рассчитать нормальные и каса­тельные напряжения в упругом полупространстве под действием статической нагрузки. Однако если пуансон находится в состоянии движения и испытывает трение с окружающей средой, то исполь­зование расчетных формул, приведенных выше, оказывается непри­емлемым. При поступательном движении пуансона (резца) схема распределения напряжений под действием вертикальной нагрузки существенно иная, чем это следует из задачи Буссинеска. В связи с относительно малыми геометрическими размерами резцов буро­вых коронок удельное давление на породу под ними можно при­нять постоянным Р(г) = const.

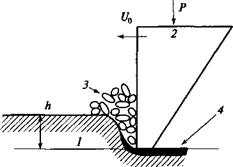
Общая схема разрушения горной породы твердосплавным инстру­ментом предусматривает первоначальное внедрение резца в породу. Дальнейшее поступательное движение резца напоминает процесс ре­зания, когда горная порода разрушается и выдавливается из образо­вавшейся лунки в виде разрушенных обломков в хрупких и упруго­хрупких породах или в виде стружки в пластичных породах (рис. 2.16).

Рис. 2.16. Схема движения резца под действием силы Р со скоростью и„: / — горная порода; 2 — резец; 3 — разрушенная порода; ‘/—зона уплотнения породы

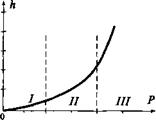
Рис. 2.17. Зависимость глуби­ны внедрения пуансона в по­роду от осевой нагрузки: /, II, III— зоны поверхностного, усталостного, объемного разрушений соответственно

Рис. 2.18. График зависимости глубины вдавливания клина в горную породу от нагрузки

Глубина внедрения резца в породу А определяется прочностью породы и осевой силой Р, которая воздействует на резец. Различают три режима разрушения горной породы при вращательном бурении: поверхностное, усталостное, объемное.

Максимальная глубина внедрения пуансона достигается при объем­ном режиме разрушения горной породы (рис. 2.17).

На рис. 2.18 показан график зависимости глубины погружения от нагрузки Р при вдавливании клина с углом при вершине 60° в хруп­кую горную породу. В начальный период происходит пластическое деформирование, и на этом участке глубина погружения пропорцио­нальна нагрузке до величины А0. Затем глубина погружения скачко­образно возрастает вследствие хрупкого разрушения до величины А,, причем погружение на эту глубину происходит при нагрузке Р, не­значительно превышающей нагрузку, соответствующую глубине по­гружения. При дальнейшем вдавливании вследствие упругой и плас­тической деформаций глубина погружения растет очень медленно вплоть до нового скачка погружения и т. д.

Рис. 2.19. Схема работы еди­ничного резца твердосплавной коронки

Таким образом, процесс разрушения гор­ных пород при вдавливании заостренных на­конечников носит скачкообразный характер.

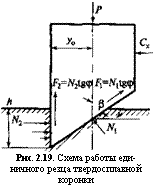
Рассмотрим работу единичного резца твер­досплавной коронки (рис. 2.19). Под действи­ем осевой нагрузки Р резец внедряется в по­роду, на лопасть резца действуют реакции по­роды и Ы2. Перемещение резца происходит по винтовой линии с углом у к горизонтали:

у = агОД, (2.72)

ио

где Vм — механическая скорость бурения; и0 — окружная скорость резца на перифе­рии породоразрушающего инструмента.

= AAroBtgp.

sin (Р + 2ф)

N^ + N пгс «ч 1

COS (j>

sinф cosp COS ф

+ sinp

COS ф 1 COS ф Подставим в выражение (2.77) значение N2 из формулы (2.74) Р COS2 ф

sin (р + 2ф)’

(2.78)

N,

р = Лг2ІЕФ+Ж| 2 cos ф ‘

sin ф COS P + sin p COS P

COS ф sin (ф + P)

Имеется в виду, что у0»ум значения угла у достаточно малы, реакции Ж, и N2 направлены нормально к передней и задней граням резца. При перемещении резца по граням возникают силы трения Л", tg ф и Ы2ф, где ф — угол трения резца о породу. Схема действующих сил находится в равновесии, спроектируем силы на вертикальную и горизонтальную оси:
= — Р + N2 tg9 + 1§ф cosp + TV, sinp = 0, Tx = N2 — iV, cosp + iV, tg9 sinp = 0. Из второго уравнения (2.73) найдем величину N2: cos (ф + р)
(2.73) (2.74) (2.75) (2.76) (2.77)
COS ф
Преобразуем (2.73):
Удельные нормальные давления при вдавливании резца на задней грани резца aN: Ол,= св sinp, (2.79) где с„ — нормальное удельное давление при вдавливании резца в по­роду: Л = ОА cos р. Тогда А
N, = o. Arsinp———— zr = АДгов tgp. 1 в к cosp Подстановка іV, из (2.80) в (2.78) дает Р COS2 ф	(2.80) (2.81)

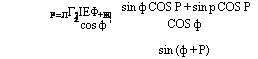Решая относительно А, имеем:

(2.82) (2.83)

Р сов2 ф

^ Агав |3 вт (Р + 2ф) ’

Н А’-Ов^Р’

где

(2.84)

сое2 ф

^ вт (Р + 2ф)’

Угол трения резца о породу ф находится в пределах от 15 до 25°, значения коэффициента т| колеблются в пределах от 0,93 до 0,97.

Формула (2.83) позволяет теоретически определить глубину вне­дрения резца в породу, которая возрастает при увеличении нагруз­ки Р, и снижается при увеличении прочности пород ст„; чем меньше угол приострения р, тем глубже величина А.

Из формулы (2.83) следует, что уменьшение угла заточки резца р способствует росту механической скорости бурения. В практике угол Р лежит в пределах 60—80°. При малых углах р наблюдаются сколы острых граней при встрече твердых включений.

В расчетной формуле (2.83) величина ств характеризует прочность породы. Если резец вдавливается в породу без вращения, то эта схема аналогична схеме вдавливания пуансона. Тогда за величину ств можно принять с достаточной степенью достоверности твердость породы по штампу — Рш.

В практике бурения внедрение резца в породу забоя осуществля­ется при вращении породоразрушающего инструмента и при умень­шенных усилиях Р. Предложенная схема рассмотрения внедрения резца этот фактор не учитывает, поэтому позволяет получить лишь качест­венную картину взаимодействия резца с породой забоя. После того как резец внедрен в породу, предложенная схема рассматривает про­цесс движения резца в горизонтальной плоскости. В начальный пе­риод движения резца передняя грань сминает (раздавливает) породу, после чего в упруго-пластичных и хрупких породах происходит ее скол. В зависимости от характера разрушения в расчетную формулу (2.83) вводятся различные значения сопротивления горных пород смятию или сколу. В установившемся режиме работы резца порода разрушает­ся последовательно в двух стадиях: смятие породы — скол.

Рис. 2.21. Распределение ин­тенсивности нагрузки под ло­пастным долотом с рассечкой

Рис. 2.20. Распределение интенсивности нагрузки под лопастным долотом

Для изучения работы породоразрушающего инструмента режущего типа первостепенный интерес представляет эпюра реакции забоя. Рассмотрим этот вопрос для лопастного долота, лопасть которого — пластина толщиной 8 и диаметром И (£>=2Я, Я — радиус). В. С. Вла­диславлев установил, что контактное давление под лопастью долота распределяется крайне неравномерно, в центральной части имеют место максимальные давления, но именно в центре лезвия горизонтальная скорость вращения лопасти равна нулю (иО|ф = 0). Это обстоятельство

является причиной того, что именно центральная часть забоя наибо­лее трудно поддается разрушению, в результате чего механическая скорость бурения падает. Для снижения такого негативного эффекта в центральной части лопастных долот делают вырез, а образующийся при этом в этой зоне столбик горной породы периодически скалы­вается в результате поперечной вибрации долота. На рис. 2.20 и 2.21 показано распределение интенсивности нагрузки под лопастным до — логом с рассечкой и без нее. Долото снабжено центральным вырезом, который позволяет снизить энергоемкость разрушения горных пород и повысить механическую скорость бурения.

Теоретически эпюра контактных давлений (<?,) описывается урав­нением гиперболы.

(2.85)

где дк — контактное давление на расстоянии Л от оси долота; т — по­казатель степени, определяется экспериментально, 0 < т <1,5.

Эксплуатация лопастных долот характеризуется неравномерным износом рабочих лопастей — более интенсивным износом периферий­ных участков. Традиционно этот недостаток компенсируется более мощным вооружением периферийных участков лопастей долота либо созданием долота, у которого бы рабочие лопасти изнашивались рав­номерно по длине.

(2.86)

Износ рабочих органов долота пропорционален работе сил трения:

д, У/ = сопе!

где и, — окружная скорость пропорциональна диаметру долота и угло­вой частоте вращения.

Расчет по формуле (2.86) затрудняется не только тем, что для раз­личных пар долото — горная порода требуется экспериментально опре­делять значения но и тем, что коэффициент трения (сопротивле­ния) также не является величиной постоянной и зависит не только
от контактных усилий, но и от окружной скорости. Геометрия ло­пастей с равномерным износом имеет конусообразную форму и с достаточной степенью точности описывается уравнением гипер­болы.

Мощность, затрачиваемая на разрушение горной породы

Разрушение породы забоя происходит при перемещении резца под действием силы вращения Сх:

Zx = — Cx + N2 + (P-N2 tgcp)tg<p, (2.87)

N2 = hAraB,

С, = hAr ов + Р tg ф — hAr oBtg ф,

Cx = hAraB(l — tgф) + />tgф. (2.88)

Отсюда крутящий момент (Н • а), с которым вращается резец, находим из следующей формулы:

Мкр = CxD/2, (2.89)

где D/2 — радиус расположения резца от оси породоразрушающего инструмента.

Известно, что между крутящим моментом и мощностью существу­ет связь:

(2.90)

где N— мощность; <в — угловая скорость.

Отсюда мощность, затрачиваемая на разрушение породы одним рез­цом, равна:

_ nCxDjri1 _ Сх Р, п

60 20 ‘ ( *U

Суммарная мощность у резцов, расположенных на различных расстояниях от центра, определяется следующим образом:

(2-92)

; = 1

Из формулы (2.91) следует, что затраты мощности на разрушение горной породы и трение инструмента о забой растут пропорциональ­но величине Сх и расстоянию от оси инструмента — D/2. В свою очередь величина Сх связана с величиной осевой нагрузки на резец Сх= КР, где А"—коэффициент трения.

Особенно значителен рост мощности от частоты вращения. Фор­мула (2.91) не учитывает затрат мощности на трение боковых лезвий резца о стенки скважины и трение резца о разрушенную породу. Однако эти затраты относительно невелики и составляют менее 10 %

от мощности, рассчитанной по формуле (2.92). Для расчетов за­бойной мощности, измеряемой в кВт, удобнее пользоваться фор­мулой

Лр. э = 5,3 • 10^Ри/)ср(0,137 + г|),

где Р — осевая нагрузка на коронку, Н; и —частота вращения корон­ки, об/мин; Др — средний диаметр коронки, м; т| — коэффициент тре­ния резцов коронки о породу забоя.

Силы трения, действующие на резец, изнашивают наиболее интенсивно режущую заостренную его часть. В результате изменя­ется геометрия резца, и для его внедрения на проектную глубину А

требуется приложить большее усилие, чем это следует из форму­лы (2.83).

Углубка коронки за оборот равна

Аоб = кт, (2.93)

где т — число основных резцов в линии резания; А —углубка основ­ного резца в породу.

Механическая скорость бурения ом (м/с) будет равна:

Им = АобЛ = Итп. (2.94)

Механическая скорость бурения при своевременной очистке забоя от шлама пропорциональна глубине внедрения единичного резца; числу основных резцов в линии «резания»; частоте вращения коронки в еди­ницу времени.

Комментарии запрещены.