Бурение грунтовых зондов, установка энергетических колодцев

Теоретические модели процесса естественного искривления скважин в анизотропных породах

Создано много теорий, объясняющих процесс естественного искрив­ления скважин в анизотропных породах. В чем-то эти теории пере­кликаются и взаимно дополняют друг друга, а где-то взаимно исклю­чают или отрицают. Исследованиями в области теории естественно­го искривления скважин в анизотропных породах занимались многие отечественные и зарубежные ученые: К. А. Боголюбский, Ю. Л. Боярко, Б. И. Воздвиженский, В. П. Зиненко, А. Г. Калинин, А. Н. Кирсанов,

Ю. Т. Морозов, В. В. Нескоромных, В. П. Рожков, И. Н. Страбыкин,

С. С. Сулакшин, В. Б. Бредли, Г. Б. Вудс, А. Лубински, Р. Т. Макла- мор, С. Е. Мэрфи, Г. М. Роллинс, Д. Б. Чисэм и др. Однако однознач­ных представлений по рассматриваемому вопросу нет ни у нас в стра­не, ни за рубежом.

Резюмируя крупный обзор исследований, выполненных учеными разных континентов, Е. Т. Браун отмечает: «Несмотря на внимание, которое уделяется данному вопросу в последние годы, существующие теории не обеспечивают удовлетворительного предсказания результа­тов искривления при вращательном бурении. Существующие теории обычно рассматривают изотропные или переслаивающиеся породы, испытывают затруднения при учете изменения конструкции долота и часто используют недостаточно определенный параметр «сопротив­ляемость бурению», который в некоторых случаях приравнивается пределу прочности пород на сжатие».

В основу теории процесса искривления в анизотропных породах почти всегда закладывается один из двух принципов, обусловливаю­щих отклонение скважины от заданного направления, суть которых сводится к следующему.

Скважины отклоняются за счет того, что скол породы под торцом породоразрушающего элемента или перед ним имеет асимметричную форму, в разных точках забоя скорость продольного перемещения коронки при резании анизотропных пород неодинакова.

Эти принципы в некоторых случаях рассматриваются вместе или обособленно.

Осколок

Плоскость слоя

Раздавленная порода

Рис. 11.35. Схема предпоч­тительного образования ос­колков в анизотропной по­роде (по Р. Т. Макламору)

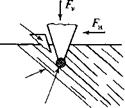Так, например, Р. Т. Макламор представляет процесс разрушения анизотропной породы следующим образом (рис. 11.35). При нагруже­нии породоразрушающего элемента силой он внедряется в породу, сжимая ее в некотором объеме. После превышения допустимых на­пряжений происходит объемное разрушение породы с образованием зоны растертой в порошок породы и осколка или осколков, отделя­ющихся вдоль плоскости сланцеватости породы. За счет взаимодей­ствия породоразрушающего элемента с ненарушенной стенкой лунки разрушения при продольном перемещении пер­вого возникает поперечная сила Рн, отклоня­ющая скважину от первоначального направ­ления в сторону восстания пласта.

Р. Т. Макламор назвал свою концепцию искривления теорией предпочтительного, или преимущественного, образования осколков.

В работах Р. Т. Макламора и В. Б. Бредли от­мечено, что концепция предпочтительного об­разования осколков применима в случае вне­дрения единичного клина в анизотропные гор­ные породы. В этих экспериментах при па­дении слоев менее 45° скважина отклонялась в сторону восстания пластов, а при углах
падения больше 45° наблюдалось отклонение в сторону падения, что радикально расходится с фактическими закономерностями естествен­ного искривления скважин. Необходимо отметить, что большинство зарубежных ученых оперирует понятием «угол падения», считая, оче­видно, скважину вертикальной в рассматриваемый момент встречи плос­кости сланцеватости. Более правильно использовать термин «угол встре­чи», поскольку он характеризует взаимное положение скважины и плоскости, что и необходимо.

Поскольку теории, подобные описанной, получили широкое рас­пространение в нашей стране и за рубежом, но базирующиеся на них выводы не всегда согласуются с практикой, были проведены экспери­ментальные исследования, преследующие цель изучить форму лунок разрушения в анизотропной породе при разных углах встречи оси ин — дентора с плоскостью сланцеватости породы.

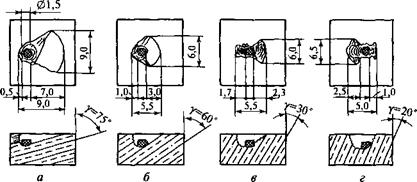
Эти исследования проводили на установке УМГГТ-3 по методике Л. А. Шрейнера. Разрушение проводили цилиндрическим пуансоном диаметром 1,5 мм. После разрушения породы лунку очищали и ее форму и размеры фиксировали измерительным микроскопом. Поро­ды были представлены лавобрекчиями, слаборассланцованными изве­стково-глинистыми алевролитами и сланцами различного состава.

Для сравнения и изучения закономерностей и конфигурации лун­ки разрушения образцы выпиливали из кернов под разными углами к плоскости сланцеватости. Некоторые типизированные профили и планы лунок разрушения анизотропных пород приведены на рис. 11.36.

Наиболее крупной по площади является лунка разрушения, полу­ченная при больших значениях угла у, равных 75° (см. рис. 11.36, а). Наибольшая часть породы скалывается по восстанию плоскости слан­цеватости, причем плоскость скола очень чистая и ровная. По паде­нию плоскости сланцеватости скалывания почти не происходит. Необ­ходимо акцентировать внимание на том, что осколок породы отделя­ется именно по плоскости делимости (сланцеватость в данном случае)

Рис. 11.36. Типизированные формы и размеры лунок разрушения в анизотропных горных породах при различных углах встречи у плоскости сланцеватости

от основания зоны смятия до выхода плоскости делимости на поверх­ность.

С уменьшением угла встречи до 60° (см. рис. 11.36,6) карти­на скалывания породы принципиально не изменяется. Осколок породы отделяется по плоскости сланцеватости, имеет ровную ниж­нюю поверхность, однако имеются и различия. Горизонтальные размеры лунки разрушения существенно меньше, чем при угле встречи 75°, а зона смятия породы находится несколько ближе к центру лунки.

Эти тенденции развиваются с уменьшением угла встречи плоско­сти сланцеватости до 30 и 20° (см. рис. 11.36, в, г). При таких углах встречи зона смятия приближается к передней стороне лунки. Боль­шая часть породы скалывается в тыльной части лунки в направлении падения плоскости сланцеватости. Передняя часть скола проработана плохо и не обладает ровной плоскостной формой.

С-374,496 СВ

Приведенные наблюдения позволяют понять основу представлений таких ученых, как Р. Т. Макламор, В. Б. Бредли и других исследова­телей, показавших теоретически и экспериментально искривление в сто­рону восстания пласта при углах встречи плоскости сланцеватости бо­лее 45° и в сторону падения плоскости сланцеватости при углах встре­чи менее 45°. Однако в анизотропных породах искривление скважин по падению плоскости сланцеватости происходит весьма редко и только при малых углах встречи 10—20°. Примером могут служить железоруд­ные месторождения Горной Шории, полиметаллические месторожде­ния Рудного Алтая, сложенные в основном анизотропными породами с субвертикальной рассланцовкой. Скважины, проектируемые с по­верхности на глубину 1000 м и более, забуривают с начальными зенитными углами не более 3—5°, поэтому углы встречи скважин с плоскостью сланцеватости в верхней части разреза имеют величину 10—30°, что согласно теориям асимметричного разрушения забоя должно приводить к выкручиванию скважин. Однако в 80—85 % случаев скважины увеличива­ют свой зенитный угол с переменной интенсивностью искривления практи­чески до выхода на линию наименьше­го сопротивления породы разрушению, причем максимум интенсивности ис­кривления происходит на равновесный угол встречи 45° (рис. 11.37).

Другие ученые допускают изображе­ние скоростей разрушения пород в раз­ных точках забоя при помощи векторов,

г Рис. 11.37. Геологическим разрез

длина которых условно принимается ш разведочной линии № 63 т£ш_

ПрОПОрЦИОНаЛЬНОЙ соответствующим ПО — тагольского железорудного место — казателям анизотропии при разрушении рождения

rh

г/г>

в

Рис. 11.38. Схема разрушения забоя и разработки ствола скважины в зависимости от направления положения породоразрушающего инструмента к плоскости напластования пород: а — перпендикулярно плоскости напластования; б— под углом 45° к плоскости напластования; в — параллельно напластованию

породы по различным осям. В стилизованном виде разрушение гор­ных пород на забое и в стенках скважины показано на рис. 11.38.

Механизм искривления ствола можно представить следующим образом. В пространстве, выбранном по контуру эпюры разрушения, торец породоразрушающего инструмента стремится занять такое поло­жение, при котором его центральная ось совпала бы с серединой овала. Инструмент передвигается в сторону наиболее интенсивно разбурива­емой стенки скважины по мере возникновения свободного простран­ства, образующегося после каждого оборота породоразрушающего инструмента, по линии наименьшего сопротивления в породе.

Изложенный подход содержит ряд спорных моментов, в связи с чем были проведены экспериментальные работы по бурению в об­разцах анизотропных пород.

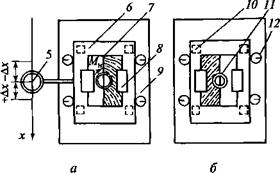
В кернодержателе 8 специального стенда (рис. 11.39) зажимали комбинированный образец горных пород 7, состоящий из изотроп­ного полукерна 1,4 и анизотропного полукерна 2, 3. Изотропный и анизотропный полукерны склеивали между собой эпоксидной смолой и располагали на стенде таким образом, чтобы направле­ния падения плоскостей сланцеватости в обоих случаях совпадали и соответствовали положительному направлению оси х, но керны имели зеркальное расположение своих изотропных и анизотропных частей.

Стенд представляет собой подвижную платформу 6, которая за счет опорных 10 и направляющих 12 подшипников может перемещаться по неподвижной платформе 9 вдоль оси х и нулевой отметки 5. При разбуривании образца анизотропной породы алмазной коронкой 11 с помощью бурового станка УКБ-50/100, входящего в состав стенда, платформа перемещается вдоль оси х, что связано с появлением попе­речных (относительно продольной оси шпинделя) сил, которые в усло­виях реальной скважины приводят к ее искривлению. Но в связи с тем что на стенде шпиндель практически не может отклоняться (поскольку представляет собой достаточно жесткую конструкцию), а платформа

Рис. 11.39. Схема экспериментального стенда для бурения в направлении падения плоскости сланцеватости (а) и в направлении восстания плоскости сланцеватости (б) и комбинированные образцы горных пород

имеет одну степень свободы, платформа с закрепленным образцом породы перемещается в направлении, противоположном естественно­му уходу скважины. При этом отход платформы от начального поло­жения в направлении +х соответствует искривлению скважины по восстанию плоскости сланцеватости, а в направлении — х соответствует искривлению по падению плоскости сланцеватости.

Анизотропные породы, использованные в данном эксперименте, были представлены в основном лавобрекчией андезитового состава порфировой структуры. Микролиты плагиоклаза составляют основную массу в вулканическом стекле. Стекло раскристаллизовано кварцем и полевыми шпатами. Размеры обломков составляют до 2,5 мм, средняя твердость породы по штампу —около 1000 МПа при весьма незна­чительном показателе анизотропии пород по твердости, равном 1,04. Однако показатель анизотропии по буримости имеет очень большое значение — 1,65.

В качестве изотропной породы использовали среднезернистый мрамор, имеющий среднюю твердость 1040 МПа. Всего было сделано 42 рейса длиной по 5 мм, в том числе 19 рейсов преимущественно в направлении падения плоскости сланцеватости (см. рис. 11.39, а) и 24 рейса преимущественно в направлении восстания плоскости слан­цеватости (см. рис. 11.39,6). При бурении в направлении падения плоскости сланцеватости образец перемещался в среднем на 0,216 мм,
т. е. скважина отклонялась в основном вдоль направления падения плоскости сланцеватости, причем из 19 раз скважина шла по восста­нию плоскости сланцеватости 5 раз, а по падению — 14 раз.

При бурении в направлении восстания плоскости сланцеватости образец перемещался в среднем на величину +0,179 мм, т. е. скважи­на отклонялась в основном по восстанию плоскости сланцеватости, причем из 24 раз скважина шла по восстанию плоскости сланцева­тости 19 раз, а по падению — 5 раз.

Полученные экспериментальные результаты позволяют поставить под сомнение асимметрию разрушения породы в забойной зоне как основополагающий фактор в процессе формирования естественного искривления скважин в анизотропных породах при алмазном бурении.

Если исходить из асимметричной формы разрушения породы как основной причины искривления скважин, то величина и направле­ние перемещения платформы в рассматриваемых альтернативных слу­чаях должны быть одинаковыми. Чем отличаются условия экспери­ментов? Полуплоскость изотропии находится с одной стороны по отношению к оси шпинделя и наклонена под одинаковым углом. Показатель анизотропии породы также одинаков в обоих случаях. Следовательно, скважина должна отклоняться всегда в направлении восстания плоскости сланцеватости, но с несколько меньшей интен­сивностью, чем это происходило бы, будь образец полностью анизотро­пен. Однако, как свидетельствуют приведенные выше результаты, этого не происходит, что позволило сформулировать иной взгляд на про­цесс естественного искривления скважин в анизотропных породах.

Обоснование искривления скважин в анизотропных породах при алмазном бурении основано на том, что для отклонения скважины от заданного направления на нее должна действовать поперечная сила. Появление этой силы не может быть объяснено асимметричной фор­мой лунки разрушения, поэтому должен быть иной принцип ее форми­рования. Эксперименты при бурении на комбинированных кернах по­зволили предположить, что искривление скважин зависит от величины

След плоскости сланцеватости

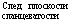
сил, действующих на породоразрушающий инструмент со стороны породы в плос­кости, перпендикулярной продольной оси инструмента.

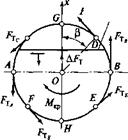
Схема силового взаимодействия по­родоразрушающего инструмента с образ­цом анизотропной породы представлена на рис. 11.40. Резец породоразрушаю — щего инструмента, перемещающийся по часовой стрелке от точки Н до G (по ду­ге HAG), движется в направлении вос-

_ „ стания плоскости сланцеватости и, таким

iTic. 11.40. Схема силовых взаи-

модействий породоразрушающего образом, вслед отдельным кристаллам, инструмента с анизотропной гор — но встречает их под разными углами, что ной породой обусловливает неодинаковую силу сопро­
тивления породы этому перемещению в различных точках. От точки G до точки Я, двигаясь по дуге GBH, резец перемещается в направле­нии падения плоскости сланцеватости, причем в точках G и Я сопро­тивление перемещению минимально (если рассматривать дугу GBH), а в точке В сопротивление наибольшее.

Сумма всех сил, действующих на коронку параллельно х, равна

AF~ = £ F~i sin р,. (11.42)

Если сопротивление породы перемещению резца в направлении восстания плоскости сланцеватости меньше, чем в противоположном направлении, то результирующая сила сопротивления AFy будет рас­положена так, как это показано на рис. 11.40, а скважина должна от­клоняться в сторону восстания плоскости сланцеватости.

Для объяснения наличия отклоняющей силы при встрече плоско­сти сланцеватости под острым углом необходимо помнить некоторые общие принципы из теории разрушения горных пород. Дифференци­руем этот процесс на составляющие и сопоставим их в условиях пе­ремещения резца в направлении восстания плоскости сланцеватости и в противоположном направлении.

Процесс алмазного бурения, как правило, сопровождается погру­жением резца в породу под действием осевой нагрузки, молекуляр­ным взаимодействием резца и горной породы, пластическим оттес­нением некоторой части породы с пути движения резца, упругой де­формацией некоторой части породы с последующим восстановлением формы и размеров выступающих частей, скалыванием породы пере­дней гранью резца и т. д. Если рассматривать величину погружения резца в породу, ориентируясь на угол встречи плоскости сланцеватости, то она должна быть одинакова для всех точек коронки (т. е. в началь­ный момент).

Силы молекулярного взаимодействия не зависят от направления вращения инструмента. Одинакова и величина пластического оттес­нения породы при различных направлениях встречи плоскости слан­цеватости, а затраты на упругую деформацию выступающих не раз­рушенных частей породы зависят от направления перемещения резца. При скольжении резца вслед наклонным кристаллам (рис. 11.41, о) вершины последних легко пригибаются и пропускают резец; при движении резца навстречу кристаллам (см. рис. 11.41,5) для пропус­ка резца вершина кристалла должна деформироваться на большую ве­личину либо должна нарушиться его сплошность. В обоих случаях затраты энергии на преодоление препятствия при перемещении резца навстречу наклонному кристаллу больше, чем при его перемещении вслед наклонному кристаллу.

Аналогично распределяются затраты энергии на скалывание не­которой части породы передней гранью резца (см. рис. 11.41, в, г). Известно, что внутри слойка породы отдельные ее элементы удержи­ваются друг относительно друга преимущественно ионно-ковалент­ными или ковалентно-ионными связями, а слойки породы притяги-

г

€

д

Рис. 11.41. Схемы взаимодействия резца и породы при перемещении резца:

а, 6— при упругом деформировании выступающих частей породы; в, г—при скалывании пород передней гранью резца; д, е — при образовании опережающей трещины с различным характером

ветвления

ваются друг к другу посредством молекулярных связей, которые на один-два порядка слабее ионных и ковалентных, что обусловливает наличие плоскостей скольжения в горных породах.

Перед передней гранью перемещающегося резца создаются нор­мальные и касательные напряжения, приводящие к отделению поро­ды в некотором объеме. Тогда при бурении в направлении восстания плоскости сланцеватости при одинаковых затратах энергии может быть отделен больший объем породы, чем при перемещении резца в на­правлении падения плоскости сланцеватости. Это объясняется тем, что в первом случае (см. рис. 11.41, в) распространение касательных напряжений при выходе на поверхность забоя соответствует направ­лениям плоскостей скольжения, что позволяет оторванным элемен­там породы выскальзывать на поверхность без особых усилий.

Другая картина наблюдается во втором случае (см. рис. 11.41, г), когда для отделения элемента породы от массива должна быть нару­шена его сплошность по линии не молекулярных, а ионных или ко­валентных связей. Кроме того, существенно затруднено удаление отде­ленной породы из-под передней грани, что в сумме приводит к появ­лению большей силы сопротивления перемещению заглубленного резца в направлении падения плоскости сланцеватости.

При рассмотрении данного процесса с позиций разных конфигура­ций трещин предразрушения при движении резца характер ветвления трещин, видимо, может оказаться различным. Можно предположить, что трещина предразрушения будет наиболее интенсивно развиваться в направлении наименьшей прочности породы, т. е. в направлении плоскостей скольжения. В таком случае наиболее предрасположенны­ми к отделению будут зоны с проработанными зеркалами скольжения при движении резца в направлении восстания плоскости сланцеватости (см. рис. 11.41, д), чем в противоположном направлении (см. рис. 11.41, е).

Естественное искривление скважин наряду с другими причинами происходит из-за избирательного фрезерования стенки скважины под­резными элементами и асимметричного разрушения ее забоя по пло­щади и глубине. Независимо от того, за счет каких причин или факторов происходит искривление, оно обусловливается наличием поперечной относительно длинной оси снаряда силы, которая стре­мится отклонить скважину от заданного направления. Если попереч­ная сила — равнодействующая множества других отклоняющих сил — отсутствует, то скважина не искривляется.

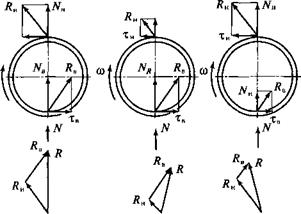
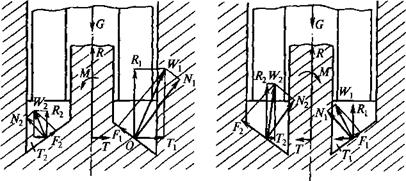
Если поперечная сила присутствует и скважина искривляется, то ал­мазная коронка (рис. 11.42, а) прижимается к стенке скважины полови­ной своей наружной боковой поверхности и половиной своей внутренней боковой поверхности — к поверхности керна, контактируя с ними свои­ми соответственно наружными и внутренними подрезными алмазами.

При этом результирующая внешних сил N формирует нормальную составляющую 7УН на наружной боковой поверхности матрицы и ана­логичную составляющую Nll на ее внутренней поверхности. При враще­нии коронки в направлении со появляются тангенциальные силы на наружной тн и внутренней тв поверхностях матрицы, действующие со стороны породы на коронку в направлении, противоположном векто­ру скорости.

Таким образом, на наружной боковой поверхности матрицы по­является равнодействующая /?„ нормальных и тангенциальных сил, приложенных к коронке и отклоняющих коронку в левую сторону от направления действия результирующей внешних сил N. На внутренней поверхности матрицы появляется соответствующая сила Лв, отклоняю­щая коронку в правую сторону от направления силы N.

Рис. 11.42. Упрощенные схемы поперечных отклоняющих усилий и возможные направления искривления скважин

00

а

б

в

В случае, когда обе поверхности матрицы несут одинаковую на­грузку, суммарная равнодействующая поперечных сил Я направлена по оси действия отклоняющей силы N. При этом уход скважины в сто­рону от этого направления отсутствует. Если какая-то из боковых по­верхностей матрицы нагружена больше другой, то сила Я разворачи­вается в соответствующую сторону: при перегрузке внешней стороны матрицы — влево (рис. 11.42,6), при перегрузке внутренней — вправо (см. рис. 11.42, в).

Направление искусственного искривления следует рассматривать в пространстве относительно вектора суммарной отклоняющей силы N. Так, если скважина естественно выполаживается равно загруженной алмазной коронкой, то при перегрузке внешней поверхности следует ожидать левого искривления. Если выполаживающаяся скважина ис­кривляется естественно вправо, то перегрузка внешней поверхности снижает интенсивность правого искривления или при определенных условиях приводит к левому искривлению. При выкручивании скважи­ны картина азимутального искривления будет обратной. Например, при повышении загрузки наружной поверхности коронки будет воз­растать правая компонента искривления и уменьшаться левая.

Величина нормальной силы N на боковой поверхности матрицы коронки пропорциональна количеству установленных на ней подрез­ных алмазов, поскольку все они воспринимают одинаковую нагрузку; величина силы т, которая фактически является силой трения, равна произведению нормальной силы на коэффициент трения, или коэф­фициент сопротивления перемещению резца при микрорезании, сильно зависящий от формы алмаза и параметров режима бурения. Это можно использовать для управления искривлением скважин, применяя ко­ронки с заранее заданными параметрами боковых поверхностей.

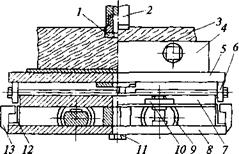
Для исследования закономерностей естественного искривле­ния скважин в анизотропных породах в Томском политехническом университете был создан специальный экспериментальный стенд (рис. 11.43), включающий основание 8, на котором на подшипни­ках 6, 9 установлены верхняя 5 и нижняя 7 подвижные платформы,

имеющие возможность перемещаться в горизонтальной плоскости. Вращению платформы препятствуют направляющие подшипники 10. На верхней платформе закреплен кернодержатель 4 с зажимными плашками и керном 3, в котором коронка 1 выбуривает отверстия с помощью станка со шпинделем 2. Возможность свободного переме­щения платформ ограничена упругими элементами 12. Около упругих элементов смонтированы индуктивные датчики 13. Неподвижность платформ при забуривании обеспечивается фиксатором 11.

Экспериментальный стенд включает буровой станок СКБ-2, промывочный насос НБ-11Э и два самопишущих милливольтметра КСП-4.

Для измерения в процессе бурения зенитной и азимутальной со­ставляющих сил смещения образца породы в качестве воспринимающе­го эти силы элемента используют упругие стальные пластины. Передача силы смещения на пластины соответствующих кареток осуществляет­ся через шарнирные упоры, закрепленные в верхних частях пластин. Величина изгиба пластины соответствует величине приложенной сме­щающей силы, и измеряют ее индуктивными датчиками, тарирован­ными в единицах силы.

Методика экспериментального бурения заключалась в том, что в кер — нодержателе закрепляли керн анизотропной горной породы, имею­щий параллельную сланцеватость. Плоскость сланцеватости устанав­ливали под требуемым углом к оси шпинделя станка. При застопо­ренных с помощью фиксатора платформах забуривали скважину на высоту матрицы коронки, затем при выключенной подаче проводили приработку алмазной коронки, необходимую для снятия напряжений в шпинделе, возникших при забуривании.

По окончании приработки коронки без остановки вращения плат­формы расстопаривали, включали подачу шпинделя при сохранении режима промывки, включали электросекундомер и самописцы, фик­сировали значения поперечных сил при установленных параметрах режима бурения. В зависимости от условий эксперимента углубку проводили либо ступенчато, либо непрерывно на всю высоту образца. Эксперимент считался состоявшимся в том случае, когда на диаграм­ме наблюдалась зона устойчивого режима, т. е. сила упругой деформа­ции пластинчатой пружины уравновешивала поперечную отклоняющую силу, генерируемую на контакте резцов коронки и горной породы.

Наличие этого экспериментального стенда позволило впервые вы­делить в чистом виде и разложить на поперечные составляющие силы, возникающие на контакте алмазной коронки и анизотропной горной породы, которые приводят к отклонению бурового снаряда от прямо­линейной траектории.

Экспериментальные исследования отклоняющих сил осуществля­ли в двух взаимно перпендикулярных направлениях в горизонтальной плоскости. Одно из этих направлений соответствовало проекции ли­нии падения плоскости сланцеватости. Силу, действующую в этом направлении, называют зенитной Р9. Если сила направлена в сторону восстания плоскости сланцеватости, она считается положительной, если в сторону падения этой плоскости — отрицательной. Силу, соот­ветствующую проекции линии простирания плоскости сланцеватости, называют азимутальной Ра. Если сила, отклоняющая снаряд, направ­лена вправо от проекции линии восстания плоскости сланцеватости, она считается положительной, если влево — отрицательной.

Экспериментальные исследования осуществляли на рассланцован — ных породах Таштагольской серии VI—IX категории по буримости при углах встречи 45° с плоскостью сланцеватости тремя однослой­ными алмазными коронками диаметром 36 мм. Основные результаты экспериментов приведены в табл. 11.4.

Таблица 11.4. Результаты экспериментального бурения Номер коронки 1 п = 325 мин 1 л = 645 мин Р, Ра Соу, МПа Р» Ра С0„, МПа л> Р» 34 0,50 2,6 4,92 1,15 2,6 2,35 2,13 7,15 1,53 4,9 7,96 2,08 3,5 5,82 1,20 7,0 12,07 -0,20 5,1 8,04 1,09 135 0,35 2,6 3,68 0,21 2,6 2,37 2,13 5,06 0,38 4,9 5,14 1,54 3,5 3,90 0,60 7,0 6,07 -0,93 5,1 7,08 -0,38 7,0 5,65 -5,80 153 0,15 2,6 4,71 0,77 2,6 4,22 0,98 7,10 -0,59 4,9 6,13 -0,06 3,5 3,32 1,72 7,0 12,81 -3,69 5,1 8,45 -0,68

Примечание, z — отношение количества алмазов на внутренней и наружной поверхностях матрицы; Соу — удельная осевая нагрузка; п — частота вращения; Рь, Р„ Ре; Ра в даН.

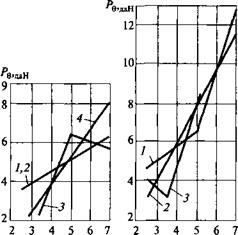
Зависимости зенитной силы от удельной осевой нагрузки при раз­ных частотах вращения, построенные на основании табл. 11.4, при­ведены на рис. 11.44. Из анализа кривых данного рисунка следуют выводы:

— отклоняющая сила, формирующая зенитное искривление, имеет абсолютную величину от 2 до 13 даН;

— зенитная отклоняющая сила, как правило, возрастает с увели­чением осевой нагрузки;

— при малых частотах оборотов эта зависимость хорошо аппрок­симируется уравнением прямой линии;

— при возрастании частоты оборотов эта зависимость менее вы­ражена, хотя в целом тенденция сохраняется;

— связь зенитной силы с частотой оборотов при проведении дан­ных экспериментов не столь однозначна, как с осевой нагрузкой;

— при частоте вращения 645 мин 1 и малых удельных нагрузках 2—3 МПа зенитная сила меньше, чем при таких же нагрузках, но при меньших частотах вращения;

—

Соу, МПа Соу, МПа Соу, МПа

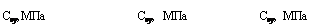
Рис. 11.44. Зависимость величины зенитного отклоняющего усилия от удельной осевой нагрузки для алмазных коронок № 34 (а), № 135 (б), № 153 (в) диаметром 36 мм при различных частотах вращения п, мин4: 1, 2— 325; 3, 4—645; /, 3 — эмпирические кривые; 2, 4 — теоретические прямые

а б в

при частоте вращения 645 мин1 и больших удельных нагрузках

4— 7 МПа зенитная сила имеет большие значения, чем при малых частотах оборотов.

В табл. 11.5 приведены корреляционные характеристики распре­деления зенитных сил, определяющие форму их связи с удельной осевой нагрузкой, степень связи этих параметров (г — коэффициент парной корреляции) и оценки степени связи параметров (/ — расчет­ная статистика и t0.0 05 — табличная статистика при t = п — 2 и уровне значимости 0,05). Поскольку все t расчетные больше t табулирован­ных, зависимости зенитной силы от осевой нагрузки описаны урав­нениями прямых линий.

Таблица 11.5. Корреляционные характеристики распределения зенитных сил Номер коронки я, мин ‘ Р„=ДСоу), дан N, шт. г t І ‘ — 0,05 34 25 Ре= 1,39Соу+ U24 33 0,496 3,18 2,04 45 /*е = 2,19Соу — 2,59 23 0,745 5,12 2,07 135 325 /“е = 0,62Соу + 2,21 37 0,335 2,11 2,03 645 Рв= 1,44Соу- 1,87 19 0,564 2,84 2,11 153 325 Рв= 1,95Соу- 1,87 36 0,735 6,30 2,03 645 />9= 1,35 Со,+ 6,56 21 0,455 2,23 2,09

При анализе закономерностей формирования азимутальной силы необходимо учитывать, что для экспериментов были выбраны алмаз­ные коронки, имеющие разное вооружение наружной и внутренней боковых поверхностей матрицы. Коронка № 34 имела соотношение количества внутренних и наружных подрезных алмазов, равное 0,5; № 135 — 0,35 и № 53 — 0,15. Для определения названного соотноше­ния боковые поверхности матриц стандартных алмазных коронок были обработаны электрохимическим способом, и обнаженные алмазы пере­считаны под микроскопом.

Из анализа рис. 11.45 можно сделать выводы о закономерностях азимутального искривления скважин:

— характер азимутальной силы очень существенно зависит от соотношения числа внутренних и наружных подрезных алмазов. При соотношении, равном 0,5, зафиксирована положительная азиму­тальная сила, равная 1,53 даН. При уменьшении соотношения алма­зов до 0,35 сила остается положительной, но ее значение уменьша­ется до 0,38 даН; при величине соотношения 0,13 преобладающей в азимутальном искривлении становится левая компонента, а сила равна 0,59 даН;

— очень активную роль при формировании азимутальной силы играет осевая нагрузка. Для всех коронок с ростом нагрузки умень­шается правая компонента и увеличивается левая. Переход от правого искривления к левому не достигнут только у коронки № 34 с соотно­шением алмазов 0,5 при частоте оборотов 645 мин’1. В пяти остальных группах экспериментов при начальной удельной нагрузке 2,6 МПа наблюдалась положительная сила (правое искривление), а при макси­мальном давлении 4,9—7 МПа — отрицательная (левое искривление);

— частота оборотов не столь существенно влияет на азимутальное отклонение, однако в целом просматривается увеличение правой ком­поненты искривления с ростом частоты оборотов.

Все изложенное позволило предположить, что отклоняющие зе­нитная и азимутальная силы связаны между собой.

Для прогнозирования азимутального усилия по материалам экспе­риментального бурения рассчитано уравнение множественной корре­ляции, связывающее величину азимутального усилия с параметрами режима бурения:

Ра= 1,03-0,046Со,+ 0,0021л. (11.43)

Между зенитной и азимутальной силами во всех случаях сущест­вует обратная зависимость, что позволяет сделать выводы относитель­но природы азимутального искривления скважин и создать систему мер по его регулированию.

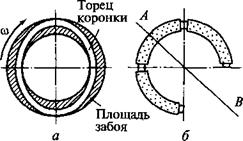
Так, на рис. 11.40 торцевые алмазы коронки в точке А движутся вслед плоскости сланцеватости, а в точке В — навстречу, что приводит к асимметричному разрушению забоя по глубине, т. е. в точке А ско­рость бурения выше, чем в диаметрально противоположной. Таким образом, в результате этого скважина должна двигаться по правому винту, т. е. выполаживаться и поворачиваться вправо по азимуту.

Рассматривая рис. 11.42, отметим, что поскольку алмазная коронка на внутренней поверхности всегда имеет меньшее количество подрез­ных алмазов, чем на наружной, то поперечные нормальные и танген­циальные силы на наружной поверхности больше, чем на внутренней. Поэтому если принимать в расчет только поперечные компоненты, скважина должна искривляться по левому винту, т. е. выполаживаться и отклоняться влево по азимуту за счет асимметричного разрушения забоя по плоскости. Однако эти поперечные компоненты начинают пре­валировать тогда, когда поперечная сила достаточно велика, т. е. вели­ка сила, прижимающая боковые поверхности матрицы к стенке сква­жины и керна.

Таким образом, при малых осевых нагрузках создается малая зе­нитная отклоняющая сила, поэтому скважина искривляется в основ­ном по азимуту вправо за счет асимметричного разрушения забоя по глубине в точках А и В (см. рис. 11.40). При наращивании осевой нагрузки увеличивается зенитная сила, возрастают нормальные и танген­циальные силы на боковых поверхностях матрицы коронки и начи­нают проявляться поперечные компоненты (см. рис. 11.42), что приводит сначала к снижению интенсивности правого искривления, а затем — к изменению направления азимутального искривления на противопо­ложное (левое).

Роль промывочной жидкости в закономерностях искривления сква­жин определяется ее способностью сохранять или увеличивать диаметр скважины. В частности, имеются утверждения о том, что увеличение расхода промывочной жидкости приводит к существенному расшире­нию скважины в призабойной зоне, сопровождаемому дополнительным перекосом колонкового набора и повышением интенсивности искривле­ния. Однако исследования, проведенные Ф. А. Вайновым и Ю. С. Ива­новым, показали, что каждая скважина, пробуренная в скальных и по — лускальных породах, имеет в призабойной зоне интервал устойчиво­сти, длина которого всегда больше 7—10 м. Диаметр скважины в этом интервале почти равен диаметру породоразрушающего инструмента. Следовательно, колонковый набор всегда работает в скважине одного диаметра, поэтому тезис о влиянии размыва стенок скважины на ин­тенсивность искривления может быть снят. Тем не менее режим про­мывки оказывает существенное влияние на искривление скважин.

Выдвинутое предположение о приоритетном характере влияния сил сопротивления породы поперечному перемещению резца при бурении в анизотропных породах на искривление скважин потребо­вало экспериментальной проверки закономерностей искривления скважин при промывке разными жидкостями.

Исследованиями П. А. Ребиндера и др. установлено, что в процес­се бурения непосредственно под коронкой образуется трещиноватая зона, и циркулирующая жидкость со смачивающим агентом прони­кает в микротрещины этой зоны. Использование промывочной жид­кости с увеличенной смачивающей способностью повышает эффек­тивность разрушения породы вследствие проникновения смачивателя в микротрещины и адсорбирования его на поверхностях. Этот эффект может активизироваться при бурении в анизотропных породах, склон­ных к образованию многочисленных плоскостей скольжения, сооб­щающихся с поверхностью забоя. В связи с этим был проведен ряд циклов экспериментального бурения рассланцованных горных пород при промывке водным однопроцентным раствором сульфонала, яв­ляющегося активным понизителем твердости, и проведено сравнение величин отклоняющих зенитных и азимутальных сил с соответствую­щими результатами, полученными при промывке скважин техниче­ской водой (табл. 11.6).

Результаты экспериментов показали, что зенитная сила уменьши­лась более чем в 2 раза, что, в свою очередь, изменило характер ази­мутальной силы. Поскольку при бурении с промывкой водой зенит­ная сила большая, то существенно проявилась левая компонента ис­кривления (поперечные эффекты), а это подтверждает сделанные ра­нее выводы.

Исследование характера влияния промывочной жидкости на искрив­ление скважин должно стать объектом серьезных исследований, ус-

Таблица 11.6. Сравнительные результаты экспериментального бурения скважин в анизотропных породах алмазными коронками диаметром 36 мм при промывке жидкостями разных типов Параметры Тип промывочной жидкости Вода 1%-й раствор сульфонола Число циклов 61 39 Соу, МПа 5,3 5,3 и, мин-‘ 325 325 Ре, даН 8,61 3,81 Ра, даН -0,72 0,78 ц„, мм/с 0,68 0,76

пешное выполнение которых откроет новые возможности управления процессом направленного бурения.

Рис. 11.46. Схема к расчету интен­сивности искривления скважин в анизотропных породах

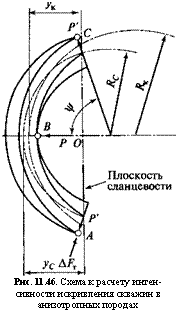Методика расчета проектной интенсивности естественного искрив­ления разработана на основании классических приемов теории сопро­тивления материалов. Она основывается на том, что в анизотропных породах за счет действия поперечной силы АРТ и других сил скважи­на резко отклоняется от первоначального прямолинейного направле­ния. В определенный момент времени при достижении предела вписы — ваемости снаряд касается стенок скважины и забоя в трех точках А, В, С (рис. 11.46). При дальнейшем искривлении скважины появляет­ся поперечный изгиб снаряда за счет действия породы на колонковую трубу в точке В с силой Р, которая пропор­циональна прогибу трубы ук. За счет уп­ругости колонкового набора сила Р пе­редается в точке А и С и воздействует на стенку скважины, причем величина силы в точках А и С равна половине силы Р.

Сила Р’ возрастает с увеличением интенсивности искривления скважины и изгибом колонковой трубы по зако­нам механики, в то время как величина смещающей силы А/7, остается постоян­ной для данных геолого-технических ус­ловий. В тот момент, когда Р’ возрас­тает до такой степени, что сравняется с отклоняющей силой Дискривление скважины должно стабилизироваться.

При этом колонковая труба вращается вокруг криволинейной оси. Другие ви­ды движения практически исключаются, поскольку снаряд зажат в резко искрив­ленном призабойном участке.

Сила Р может быть легко рассчитана исходя из упругих свойств колонковой трубы:

Р=ук48Е1/1 (11.44)

где ук — величина наибольшего прогиба трубы; Е — модуль упругости; /—момент инерции сечения трубы; / — длина колонковой трубы. Радиус искривления скважины будет равен

«c = /2/8jc, (П.45)

где ус — наибольший прогиб скважины на отрезке, равном /.

Выразим прогиб оси скважины через величину прогиба оси трубы:

yc = y^ + Ar{ +cosi|/), (11.46)

где |/ — угол смежности точек В и С; Аг — радиальный зазор между колонковой трубой и скважиной.

Поскольку у в реальных условиях не превышает нескольких гра­дусов, запишем

Ус~Ук + AD, (11.47)

где AD — диаметральный зазор между колонковой трубой и скважиной. Решаем уравнение (11.44) относительно ук, приравнивая ДFT к Р/2:

рл F

Подставим выражение (11.46) в равенство (11.45) и решим урав­нение относительно ук:

yK=W~AD — {пл9)

Приравняем правые части уравнений (11.48) и (11.49) и решим уравнение относительно Rc:

Re = ———— ——— —- (11.50)

‘ A F, P

AD +

24 El

Далее определяем интенсивность естественного искривления скважин:

19,05

ЛАП АЕРЛ

24 AD +

EI

/ =——— ——————— (11.51)

где АБ — диаметральный зазор, м; Ді^т — отклоняющая сила, даН; I — длина колонковой трубы, м; Е— модуль Юнга, даН/м2; /—момент инерции сечения трубы, м4.

626

Из последнего уравнения следует, что возможно наличие экстре­мума длины колонковой трубы, обеспечивающей минимальную ин­тенсивность искривления. Для отыскания экстремума продифферен­цируем уравнение (11.51) относительно длины: приравняем первую производную нулю и решим полученное уравнение относительно длины:

Л си	48ДЯЇ ЕІ р у
(11.52)

(11.53)

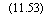
/о =

48£7ДО

АБТ

где 10 — длина колонковой трубы, обеспечивающая минимальную ин тенсивность искривления.

/, град/м Рис. 11.47. Зависимость интенсив­ности искривления скважин от дли­ны колонкового набора диаметром 73 мм при отклоняющей силе 10 даН:

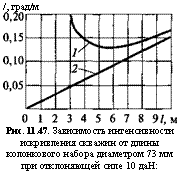Проиллюстрируем графически экст­ремальный характер уравнения (11.51), проведя расчеты интенсивности искрив­ления для колонковых труб диаметром 73 мм и дезориентирующей силы 10 даН (рис. 11.47).

Уравнение (11.51) для полностью сцентрированной в скважине колонко­вой трубы, при диаметральном зазоре, равном нулю, преобрело вид

. 19,05 Д/У

(11.54)

ЕІ

1 — стандартный колонковый набор; 2 — сцентрированный в скважине ко­лонковый набор

Решим его для тех же усилий, что и предыдущее. Полученная линейная за­висимость интенсивности искривления от длины трубы изображена на рис. 11.48.

Из уравнения (11.54) видно, что с увеличением длины центрированного ко­лонкового набора возможная интенсивность искривления возрастает, поскольку длинный снаряд прогнуть проще, чем короткий.

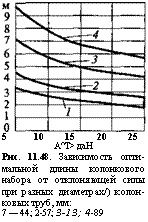
Уравнение (11.53) позволяет определить оптимальную длину ко­лонкового набора, которая обеспечивает наименьшую интенсивность естественного искривления скважин при разных дезориентирующих силах (табл. 11.7, рис. 11.48).

Экстремальный характер зависимости интенсивности искривле­ния скважин от длины колонковой трубы показан на рис. 11.40. При увеличении длины колонковой трубы с 1 до 4,5—5 м интенсивность искривления уменьшается от 0,08—0,1 до 0,01—0,03 град/м. Таким образом, оптимальная длина колонкового набора находится в пре­делах 4,5—5 м, что достаточно хорошо согласуется с расчетами (см. табл. 11.7).

/е, град/м Рис. 11.49. Эмпирическая зависимость интенсивности зенитного искривления от длины 73-миллиметровой колонковой трубы при бурении скважин на Шере — гешевском и Таштагольском месторож­дениях

Таблица 11.7. Оптимальные длины (м) колонковых наборов различных диаметров Диаметр колонковой трубы, м Дезориентирующая сила, даН 5 10 15 20 25 0,044 3,30 2,62 2,29 2,06 1,91 0,057 4,45 3,53 3,09 2,81 2,61 0,073 7,12 5,66 4,94 4,94 4,17 0,089 9,70 7,70 6,73 6,11 5,68

5 10 15 20 25 А^Т> даН Рис. 11.48. Зависимость опти­мальной длины колонкового набора от отклоняющей силы при разных диаметрах/) колон­ковых труб, мм: 7 — 44; 2-57; 3-13; 4-89

Во многих работах отмечается, что при бурении скважин комп­лексами ССК и КССК интенсивность искривления в 1,2—1,5 раза выше, чем при алмазном бурении с использованием обычной колон­ны и соответственно обычного колонкового набора.

Выполним расчет предельной интенсивности естественного искрив­ления по уравнению (11.51) для разных снарядов со съемными керно- приемниками и стандартных труб соответствующей длины, при удель­ной отклоняющей силе Д^т = 0,031 МПа позволим получить данные, приведенные в табл. 11.8.

Анализ их показывает, что интенсивность искривления скважин с применением ССК и КССК всегда выше, чем при бурении обыч­ным снарядом. Это объясняется тем, что прирост отклоняющей силы за счет утолщения матрицы не компенсируется повышенным мо­ментом инерции более толстой колонковой трубы названных комп­лексов.

Превышение расчетной интенсивности искривления для ССК и КССК над обычными снарядами составляет до 31 % (см. табл. 11.11), причем наибольшее превышение наблюдается при использовании КССК-76, что объясняется наибольшей площадью торца колонки у на­званного комплекта. Фактически разница в интенсивности искривления

Таблица 11.8. Предельная интенсивность естественного искривления скважин для комплексов снарядов со съемными керноприемниками (ССК, КССК) и для стандартных колонковых наборов Типо­ размер снаряда Длина колон­кового набо­ра, м Диаметр коронки, 10~2 м Площадь торца коронки, 10-4 м2 Откло­ няющая сила, даН Диаметр колонковой трубы, 10"3 м Момент инерции сечения колон­ковой трубы, 10-* м* Диамет­ральный зазор, 10-3 м Пре­ дельная интен­ сивность искрив­ ления, град./м наруж­ ный внут­ ренний наруж­ ный внут­ ренний ССК-46 3,90 46 24 12,09 3,75 44 35 11,2 2 0,184 СКН-46 3,90 46 31 9,1 2,84 44 37 9,4 2 0,173 ССК-59 5,40 59 35 17,5 5,42 56 45 28,7 3 0,145 СКН-59 5,40 59 42 13,5 4,22 57 48 26,0 2 0,115 ССК-76 4,19 76 48 27,3 8,45 73 60 77,2 3 0,122 СКН-76 4,19 76 59 18,0 5,62 73 63 63,0 3 0,114 ССК-76 6,72 76 40 32,7 10,14 73 60 77,2 3 0,115 СКН-76 6,72 76 59 18,0 5,62 73 63 63,0 3 0,088

при бурении стандартным колонковым набором может быть еще более заметной, если интенсивность искривления рассчитать на оптималь­ную длину.

Традиционные технические средства направленного бурения часто не способны обеспечить эффективность стабилизации траекторий сква­жин в анизотропных породах. Это связано с тем, что применяемые жесткие компоновки низа бурильной колонны обладают малой чувст­вительностью и генерируют усилия в направлении, противоположном естественному искривлению, только после большого изгиба.

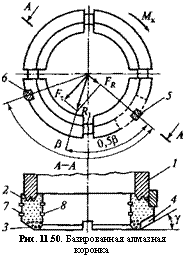
Рис. 11.50. Базированная алмазная коронка

Корректировка траекторий скважин с помощью раскрепляемых отклоните­лей позволяет, как правило, вывести скважину в заданную точку. Однако этот метод нельзя считать конструктивным, поскольку он предусматривает исправ­ление уже допущенного брака и требует для этого определенных дополнительных затрат средств и времени. В связи с этим возникла необходимость разработки ин­струмента, предназначенного для стаби­лизации траекторий скважин, основан­ного на других принципах, т. е. за счет учета характера взаимодействия есте­ственных сил, возникающих при кон­такте породоразрушающего инструмен­та с горной породой.

Вид базированной алмазной корон­ки и ее продольное сечение представ­лены на рис. 11.50. Коронка состоит
из корпуса 1, к которому присоединена металлокерамическая матри­ца 2, содержащая естественные или искусственные объемные алмазы 3. Наружная часть торца корпуса наклонена под углом у к поперечной оси. В наклонной части торца матрицы выбран паз 4, горизонтальная про­екция которого показана пунктиром. В боковую поверхность матрицы вмонтированы базовые направляющие 5 и 6. Боковые поверхности матриц армированы наружными 7 и внутренними 8 подрезными ал­мазами. Базовые направляющие разнесены на угол р. Наружная по­верхность матрицы коронки, заключенная между сторонами угла р, подрезными резцами не армирована. При создании осевой нагрузки и крутящего момента осуществляется силовое взаимодействие торца коронки и горной породы. На наклонной части торца коронки в точ­ке касания каждого алмаза с породой возникает поперечная радиаль­ная составляющая, направленная к центру коронки. Поперечные силы, генерируемые в диаметрально противоположных точках, взаимно унич­тожаются. Поскольку в матрице выбран паз, диаметрально проти­воположная ее часть формирует некомпенсированные радиальные силы, равнодействующая которых FR направлена к центру паза. В точке, диаметрально противоположной пазу, формируется и FT — равнодей­ствующая тангенциальных сил, направленная противоположно векто­ру скорости вращения.

Равнодействующая R радиальной и тангенциальной сил направле­на по биссектрисе угла р и обеспечивает равномерную загрузку базо­вых направляющих и их равномерный износ. Коронка прижимается к стенке скважины базовыми направляющими, имеющими гладкую форму, которые не разрушают стенку скважины и не уводят скважину от заданного направления.

При появлении посторонней возмущающей силы, вызванной геоло — го-техническими причинами, величина и направление равнодействующей всех поперечных сил меняется, но не выходит за пределы сектора, ог­раниченного базовыми направляющими, что исключает возможность прижатия матрицы ее вооруженной частью к стенке скважины и резко

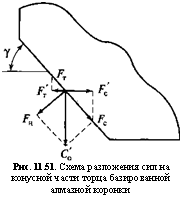
Рис. 11.51. Схема разложения сил на конусной части торца базиро­ванной алмазной коронки

снижает интенсивность увода скважины от первоначального направления.

На рис. 11.51. приведена схема раз­ложения сил на наклонной конусной части торца базированной алмазной ко­ронки. Обозначены силы: С’0 — несбалан­сированная осевая нагрузка; FH — нор­мальная составляющая от С0′, действую­щая перпендикулярно плоскости торца коронки; Fc — сила, смещающая корон­ку по падению плоскости резания; FT — сила трения, препятствующая этому сме­щению; FT’ Ц Fc’ — проекции соответст­вующих сил Fc и Fr на горизонтальную плоскость.

Несбалансированную радиальную силу FR определяют как разницу сил FT’ Ц Fc’. Ее величину находят из несложных уравнений:

/V = С0’sin у; (11.55)

Fc= С’0 cos у; (11.56)

FT = FT cos у = C’0 sin у cos у; (11.57)

Fc = Fcq>, (11.58)

где ф — коэффициент трения при перемещении резца в плоскости продольного сечения коронки,

Fc’ = Fc cos у = С’ ф cos2 у. (11.59)

Тогда

Fr = С о sin у cos у — С’ ф cos2 у = С’ cos y(sin у — ф cos у). (11.60)

Из уравнения (11.60) следует, что радиальная сила появляется в тот

момент, когда sin у > cos у • ф и может регулироваться углом наклона торца коронки и несбалансированной осевой силой, если считать ве­личину ф константой.

Несбалансированная тангенциальная сила равна

= С0’/cos у, (11.61)

где / — коэффициент трения при перемещении резца в плоскости забоя.

Методика определения угла разноса и местонахождения базовых направляющих основывается на следующих положениях.

1. Для того чтобы базовые направляющие нагружались равномерно и, следовательно, имели одинаковый износ, равнодействующая всех по­перечных сил должна быть направлена по биссектрисе угла между ними.

2. Одна из базовых направляющих располагается на линии дейст­вия несбалансированной радиальной силы, что исключает возмож­ность фрезерования стенки скважины при малых значениях танген­циальных сил.

Определить величину угла р можно, вернувшись к схеме, приве­денной на рис. 11.50:

Р = 2 arctg — р-. (11.62)

Fr

Подставив уравнения (11.61) и (11.60) в выражение (11.62), полу­чим уравнение для расчета угла р:

/

(3 = 2 arctg ——————- . (11.63)

вшу-фсову v ’

Создание коронок с эллиптической матрицей и незамкнутым торцом является перспективным направлением технических средств для снижения интенсивности естественного искривления скважин.

Было предложено с целью снижения интенсивности искривления скважин при бурении снарядами со съемными керноприемниками со­здавать матрицы, позволяющие бурить скважины на малых (до 6 кН) осевых нагрузках.

Снижение необходимых осевых нагрузок на коронку без умень­шения удельных осевых нагрузок может достигаться разработкой оригинальных конструкций матрицы (схема размещения и круп­ность алмазов, состав матрицы) или сокращением площади торца коронки.

Особенностью коронки, предлагаемой для снижения интенсивно­сти искривления, считается наличие эллиптической кольцевой фор­мы рабочей части (рис. 11.52, а), причем большая ось эллипса по наружному контуру равна диаметру формируемого ствола скважины, а малая ось по внутреннему — диаметру керна. Эллиптическая форма торцевой части позволяет создать коронки со сколь угодно малой пло­щадью торца без изменения конструкции колонкового набора, по­скольку при этом формируются ствол скважины и керн, имеющие обычные диаметры.

Использование коронки с незамкнутым торцом матрицы (рис. 11.52, б) заключается в следующем. Несовпадение центра тяжести торца мат­рицы с точкой приложения осевого усилия приводит к появлению изгибающего момента, постоянно действующего по линии АВ незави­симо от вида движения коронки и стремящегося ориентировать след плоскости изгиба колонкового набора по этой линии.

В этом случае, когда под действием геологических или других при-чин колонковый набор приобретает фиксированный перекос и вращается вокруг собственной оси, он сообщает этот вид движения породоразрушающему инструменту. При использовании обычной ко­ронки в такой ситуации происходит максимальное искривление сква­жины.

При вращении коронки с незамкнутым торцом в таком режиме плоскость действия изгибающего момента, обусловленного ее конструк­тивными особенностями, будет вращаться с частотой, задаваемой по-

Рис. 11.52. Схемы коронок неправильной формы: о —коронка эллиптической кольцевой формы; б—коронка с незамкнутым торцом

родоразрушающему инструменту станком, и стремиться задать первой полуволне колонкового набора вращение вокруг оси скважины. Это сокращает время работы компоновки в режиме фиксированного пере­коса и уменьшает интенсивность искривления скважины.

В Томском политехническом университете были проведены экс­периментальные и теоретические исследования, позволившие дать ре­комендации по управлению процессом искривления скважин в ани­зотропных породах технологическими методами, в том числе балан­сированными коронками.

При бурении скважин наиболее универсальным показателем процес­са взаимодействия резца с породой считается энергоемкость (в Дж/мм3), которую определяют уравнением

(11.64)

где УУ— мощность, затраченная на разрушение горной породы, Вт;

5— площадь кольца разрушенной породы, мм2; ум — механическая ско­

рость бурения, м/с.

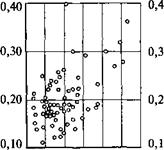
Коэффициент трения / можно увязать с энергоемкостью а., про­цесса бурения (рис. 11.53).

Проведенный корреляционный анализ подтвердил сделанное пред­положение. Корреляционные уравнения, связывающие коэффициен­ты трения однослойных /0 (1, 3) и импрегнированных /и (2,4) коронок с энергоемкостью (рис. 11.54), имеют вид

/0 = 0,094+ 0,025в,; (11.65)

/

/и = 0,143 + 0,029а„. (11.66)

Рис. 11.53. Точечные диаграммы распределения коэффициента трения / от энергоемкости разрушения а0: о — для однослойных коронок; 6—для импрегнированных коронок

о о о о о э   о о < < о о У я О оо О4′ о о   О1 о сю >о «0* 1

2345678 01234567 а„, Дж/мм3 ау, Дж/мм3 а б

/

В уравнениях (11.65), (11.66) имеется свободный член большой величины, при­чем этот член не связан непосредственно с разрушением породы. Складывается мне­ние, что этот член — некая начальная вели­чина коэффициента трения, не зависящая от параметров разрушения, обусловленная наличием сил молекулярного взаимодей­ствия резца и породы.

0,5 1,5 2,5 3,5 4,5 5,5 6,5 7,5 Дж/мм3 Рис. 11.54. Зависимости коэф­фициента трения / от энергоем­кости а0 процесса разрушения породы:

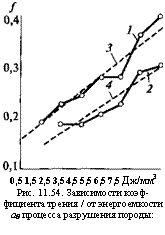Этот свободный член, как показали эксперименты, имеется всегда, и значение его находится на уровне 0,1. Еще не уда­валось получить коэффициент трения, рав­ный 0,05 или 0,07 даже при самых малых затратах мощности. Он всегда больше 0,1. Видимо, этот порог существует объективно.

/ — экспериментальная для импрег — нированной коронки; 2 —то же, для однослойной коронки; І —теорети­ческая для импрегнированной корон­ки; 4 — то же, для однослойной ко­ронки

Другой же член уравнения непосред­ственно связан с разрушением породы, т. е. ее резанием, смятием, скалыванием, упругим и пластическим деформировани­ем. Его значение определяется соотноше­нием усилий, затраченных на проворачи­вание вдавленного резца и на это вдавли­вание.

Для практического определения и прогнозирования величины коэффициента трения необходимо установить его связь со свойст­вами горных пород и параметрами режима бурения. Эта задача была решена опосредованно через энергозатраты на разрушение горной породы.

Энергоемкость процесса разрушения (Дж/мм3) теоретически мо­жет быть записана следующим образом (по И. А. Нейштетеру):

я„= 6-Ю-5-^-, (11.67)

где С0 — осевая нагрузка, даН; я —частота вращения, мин1; Др— средний диаметр коронки, мм; им — механическая скорость бурения, м/ч.

Проведенный анализ показал, что характер зависимости энерго­емкости от режимных параметров значительно отличается в породах средней твердости и в твердых породах. Поэтому искомые зависимо­сти механической скорости определялись для пород средней твердо­сти (Н< 3500 МПа) и твердых (Н> 3500 МПа) отдельно, а также от­дельно для однослойных и импрегнированных коронок.

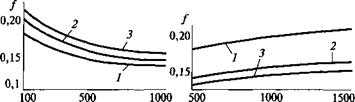
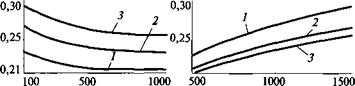
С помощью уравнений (11.65), (11.66) можно рассчитать коэффи­циенты трения для разных параметров режима бурения скважин одно­слойными и импрегнированными коронками диаметром 76 м в твер­дых породах (#= 5000 МПа). Эти зависимости приведены на рис. 11.55.

п, мин

-1

Со; даН

/

в

п, мин

-1

С„, даН

Рис. 11.55. Зависимости коэффициента трения / от частоты вращения п и осевой нагрузки С0 для однослойных (а, б) и импрегнированных (в, г) коронок:

/

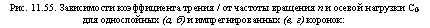
а, в — С0 = 500 (/), Ю00 (2), 1500 даН У);

б, г — п= 100 (7), 500 (2), 1000 мин’1 (5)

Анализ графиков на рис. 11.55 позволил сделать следующие выводы:

1. С ростом осевой нагрузки на резец коэффициент трения уве­личивается. Акцентируем внимание на том, что увеличивается не сила трения, а коэффициент трения. Объясняется это тем, что чем боль­ше осевая нагрузка на резец, тем больше его заглубление в породу. При этом у всех кривогранных кругловершинных образований, к кото­рым относятся алмазы, прирост горизонтальной проекции заглубленной части меньше, чем соответствующий прирост вертикальной проекции.

2. С ростом частоты вращения коэффициент трения снижается. Это объясняется тем, что с ростом частоты вращения снижаются за­траты на вторичную упругую деформацию отдельных элементов гор­ной породы, так как они не успевают восстановить свою форму, поэтому суммарные затраты на срез уменьшаются. Эта мысль отмеча­лась в свое время в работе И. А. Остроушко: «Могут быть такие ско­рости смещения, при которых упругие деформации неровностей не будут успевать разряжаться полностью, и в этом случае затраты рабо­ты на трение и износ должны быть ниже». Кроме того, при повыше­нии скорости резания уменьшаются затраты на пластические деформа­ции и уменьшается количество выделяемой теплоты. Все это приводит к уменьшению энергоемкости процесса разрушения породы и сниже­нию коэффициента трения.

3. У импрегнированных коронок коэффициент трения о горную породу выше, чем у однослойных, поскольку они армируются дробле­ными алмазами, которые при равных условиях внедряются в породу на большую глубину, чем овализованные алмазы однослойных коронок.

Коронки специальной геометрии, предложенные Ю. Л. Боярко, пред­назначены для пространственного искривления скважин в анизотроп­ных породах. Ориентация снаряда при их применении не требуется, однако предварительно надо определять величину и направление век­тора анизотропии горных пород.

Если рабочую поверхность коронки выполнить таким образом, чтобы рабочие поверхности режущих элементов образовали внутрен­ний или наружный конус, тогда при пересечении анизотропных гор­ных пород под острым углом к оси снаряда будет происходить нерав­номерное разрушение пород забоя (рис. 11.56).

Режущие элементы коронок с внутренней рабочей поверхностью, проходящие перпендикулярно сланцеватости или близко к этому, встре­чают меньшее сопротивление, чем проходящие параллельно сланце­ватости. В результате этого возникают неравные реакции ТУ, и Ыг, перпендикулярные рабочим поверхностям, причем ТУ, > Л^.

Силы Г1 и /’’з препятствуют скольжению рабочих поверхностей по горной породе. Для того чтобы при работе породоразрушающего инструмента происходило разрушение горной породы в направле­нии действия нормальных составляющих УУ, и М, необходимо, чтобы силы ^ и Р2 по своей величине превосходили или были равны соот­ветствующим силам трения рабочих элементов по горной породе, т. е.

р>^’,

Сила трения

Ртр = М1ё<9, (11.68)

где ф — угол трения (здесь и далее терминология Ю. Л. Боярко) поро­доразрушающего инструмента по горной породе.

а б Рис. 11.56. Схема искусственного искривления скважин коронками специальной геометрии

Поэтому угол наклона рабочей поверхности к оси породоразру­шающего инструмента необходимо брать равным 90° ±<р. Отсюда ка­сательные силы Т7! и Р2 определяют из следующих выражений:

Рх = Их ф; Р2 = N. гё ф.	(11.69) (11.70)

Результирующие рассмотренных сил реакции пород Ц/Г1 и 1¥2 в об­щем случае направлены под острым углом к оси бурового инструмента. В свою очередь, их можно разложить на силы Л, и Л2, направленные по оси снаряда и перпендикулярные этой оси, Г, и Т2. Приведение этих сил к точке О дает осевую реакцию Я, опрокидывающий мо­мент М и сдвигающую силу Т.

В связи с этим происходит поворот бурового снаряда вокруг точ­ки О, причем реакция Я в этом процессе не участвует. Опрокидываю­щий момент М отклоняет верхнюю часть инструмента от оси скважи­ны, а радиальная сила Т уводит от оси нижнюю часть. Эти совместные усилия направляют буровой снаряд в направлении восстания плоско­сти сланцеватости, если коронка имеет внутренний конус, наклонен­ный под углом 90°+ ф к оси инструмента (см. рис. 11.56, а).

Чтобы скважина могла искривляться в сторону падения плоскости сланцеватости, необходимо применить коронки с внешней конической рабочей поверхностью с углом наклона образующей к оси инструмен­та 90° — ф. В этом случае на режущих элементах возникают неравные реакции и Ы2, перпендикулярные рабочей поверхности, и Р1 и Ръ параллельные ей. Силы реакции забоя Л, и Я2 имеют направление, параллельное оси бурового инструмента, и, приведенные к точке О, дают осевую силу реакции К и опрокидывающий момент М (см. рис. 11.56, б).

Таким образом, породоразрушающий инструмент, имеющий угол наклона образующей рабочей поверхности 90° ± ф, может быть приме­нен для направленного бурения скважин в анизотропных горных поро­дах. Ниже приведены значения угла ф (град.) для разных групп пород.

Горные породы Твердосплавная коронка Алмазная коронка

TOC o "1-5" h z Осадочные………………………………………. 20 22

Изверженные………………………………………. 15 17

Метаморфические…………………………………. 6 8

Комментарии запрещены.