Бурение грунтовых зондов, установка энергетических колодцев

Отличительными особенностями технологии бурения скважин плавлением горных пород, включая снежно-фирновые и ледовые толщи, являются высокая концентрация в зоне забоя тепловой энергии, эффективная ее передача породе (снегу, фирну, льду) для обеспечения заданной скорости плавления, удаление образующе­гося расплава из зоны забоя с формированием из него или его части на стенках скважины монолитного и прочного покрытия. Передача тепловой энергии к поверхности плавления забоя сква­жины может осуществляться контактной теплопередачей, конвек­цией и излучением. В настоящее время широкое применение при бурении скважин получило контактное плавление.

Для многочисленных физических явлений и технологических процессов, сопровождающих контактное плавление твердых тел, характерно наличие нагревательного устройства с теплопередаю — щей рабочей поверхностью и собственно твердого тела (горной по­роды, ледяного массива) с поверхностью плавления, механическое и тепловое взаимодействие которых осуществляется через движу­щийся между ними под действием внешних сил слой расплава (воды). Несмотря на распространенность, этот сложный многопа­раметрический процесс остается теоретически недостаточно полно исследованным, особенно это относится к бурению скважин плав­лением. Имеющиеся по этому поводу решения [13, 18, 23, 72] часто основаны на простых балансовых соотношениях, которые, несмотря на правильное в целом описание основных закономер­ностей изучаемого процесса, не позволяют детально исследовать ряд эффектов и учесть влияние многих практически значимых факторов, в частности влияние формы рабочей поверхности нагре­вательного устройства (пенетратора), рассеивание теплоты в слое расплава, неизотермичность рабочей поверхности нагревателя и др.

Изучение процесса бурения скважин плавлением с целью обос­нованного выбора его определяющих параметров, разработки и со­вершенствования технических средств, повышения эффективности их работы невозможно без математического моделирования, по­строения достаточно общей замкнутой модели контактного плавле­ния, оценки значимости и целесообразности учета тех или иных факторов с целью упрощения основных уравнений, описывающих тепломассоперенос в зоне забоя скважины. Построение на этой основе новых математических моделей различных классов точности позволит провести предварительный качественный и количествен­ный анализ процесса бурения скважин плавлением, эффективно рассчитать его разнообразные технологические режимы, обеспечить оптимальную конструкцию нагревательных устройств (пенетраторов) и обосновать рациональный режим их ра­боты.

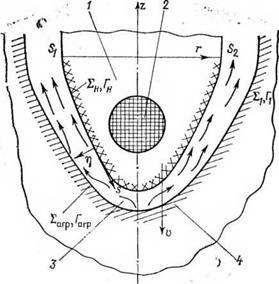
Рис. 4.1. Схема для математического моделирования процесса бурения скважин плавлением в ледовых толшах. 1 — корпус нагревательного устройства; 2 — тепловой электрический элемент; 3—вода; 4 — лед

Процесс бурения скважин плавлением может быть схематизи­рован следующим образом (рис. 4.1). В нагревательном устрой­стве (пенетраторе), имеющем форму сплошного цилиндра или цилиндрического кольца, равномерно распределены источники тепла, благодаря которым твердая непроницаемая рабочая поверх­ность устройства 2„ разогрета до температуры ta, превышающей температуру плавления ^агр твердой среды, заполняющей конеч­ную область £2 трехмерного пространства с подвижным участком границы — поверхностью плавления забоя скважины 2агр.

Выше рабочей поверхности нагревательного устройства (пене- тратора) на стенках скважины формируется слой застывающего расплава с поверхностью Нагревательное устройство (пенетра — тор) углубляется в расплавленную твердую среду с некоторой скоростью v, выдавливая образующийся расплав в зазор между поверхностями 2Н и 2агр под действием внешней нагрузки G (силы веса), приложенной к пенетратору и рассчитанной на еди­ницу площади его миделевого сечения.

С практической точки зрения важны установившиеся режимы бурения плавлением с постоянной скоростью углубки скважины (v = const). Для построения математической модели процесса тепломассопереноса в криволинейном слое расплава воспользуем­ся общими балансовыми уравнениями сохранения массы, коли­чества движения и энергии. Записанные в интегральной форме,[56] уравнения сохранения массы, количества движения и энер-

гии имеют вид

о

5 P»wiw„do== РжРdz—^pndo — j — ^ T„da

X	a	a
О

5 РжЕ^п dx=^qndo + ^Ф di,

T

о

a

где a—поверхность, ограничивающая элементарный объем рас­плава; wn — проекция вектора скорости течения расплава w на внешнюю нормаль п к поверхности a; Е — внутренняя энергия; р— давление в слое расплава; qn— проекция плотности теплового по­тока q на нормаль к поверхности а; рж — плотность жидкой фазы; Ф — диссипативная функция, характеризующая работу внутрен-

*>•

них сил; F—массовая сила; тп — сила поверхностного натя­жения.

Для замыкания системы (4.1) ее необходимо дополнить урав­нениями, описывающими состояние расплава, связь внутренней энергии с температурой, температурные поля в твердой фазе среды и в теле нагревательного устройства, а также определить краевые условия. Предполагая, что расплав — несжимаемая, однородная жидкость, в качестве уравнения состояния можно принять рж = = const. Внутренняя энергия с точностью до константы может быть определена из равенства Е — сж<ж, где сж и tK — удельная теплоемкость и температура расплава. Распределение тем­пературы в твердой фазе среды может быть задано уравнением стационарной теплопроводности, которое в подвижной системе координат, связанной с рабочей поверхностью нагревателя, имеет вид

pTcTv grad tr + div (Ят grad tT) = 0,

где £г, рт, ст и кт — соответственно температура, плотность, коэф­фициент удельной теплоемкости и коэффициент теплопроводности твердой фазы среды.

(4.3)

В нагревательном устройстве при установившемся режиме плавления температурное поле описывается уравнением

div (Лн grad f„) + qv = 0,

где <71/ — объемная плотность источника тепла; Хн — коэффициент теплопроводности материала нагревателя.

Вид граничных условий для системы (4.1) в общем случае за­висит от конкретных особенностей технической реализации про­цесса контактного плавления. Однако при этом условии на по­верхностях 2„ и ЕагР остаются без изменения следующие пара­метры:

2) на границе расплав — твердая фаза среды ‘агр

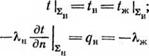
1) на границе рабочая поверхность пенетратора—расплав

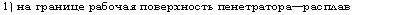
(4.4>

(4.5)

где — удельная теплота плавления; и„ — проекция вектора ско­рости углубки и на нормаль к поверхности 2агр;

SHAPE \* MERGEFORMAT

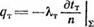
‘агр

(4.6)

— плотность теплового потока, поступающего в плавящуюся среду с поверхности Еагр.

Уравнения (4.1) и соотношения (4.2) — (4.6) являются основой общей математической модели, описывающей явления тепломассо — переноса при квазистационарном режиме контактного плавления.

Эффективным средством качественного анализа общей мате­матической модели процесса контактного плавления при бурении скважин для построения более конкретных упрощенных моделей являются методы теории подобия и анализа размерностей. Анализ характерных масштабов физических величин и выбор определяю­щих параметров, описывающих исследуемый процесс, позволяют привести уравнения модели к безразмерному виду, найти основ­ные критерии подобия и оценить значимость и целесообразность учета тех или иных факторов в рассматриваемом классе задач.

Применяемые на практике при бурении плавлением разнооб­разные нагревательные устройства (пенетраторы) обладают, как правило, осевой симметрией и конструктивно разделяются на два типа: для бурения сплошным забоем — рабочая поверхность 2Н с осевой симметрией и образующей Гн; для бурения кольцевым за­боем с отбором керна — криволинейная рабочая поверхность, один из размеров которой достаточно велик по сравнению с двумя дру­гими характерными размерами. В первом случае течение и тепло­обмен в слое расплава имеют существенно радиальный характер, а во втором при небольшой радиальной ширине кольцевого пене­тратора и малой толщине слоя расплава можно пренебречь эффек­тами, связанными с осевой симметрией, и рассматривать плоскую задачу.

Относительно малая толщина слоя расплава по сравнению с ха­рактерными размерами пенетратора позволяет по аналогии с тео­рией пограничного слоя существенно упростить исходную матема­тическую модель, используя одномерные балансовые уравнения сохранения массы, количества движения и энергии, записанные в
форме интегральных соотношений для осредненных по толщине слоя характеристик процесса переноса [65]. Кроме того, используя методы теории подобия, можно исключить из этих уравнений сла­гаемые, учет которых в каждом конкретном случае не повышает точности решения задачи.

Для удобства анализа осесимметричной и плоской задач кон­тактного бурения плавлением (для сплошного и кольцевого забоя скважины) введем связанные с пенетратором системы цилиндри­ческих (плоских декартовых) z, г и криволинейных s, г] коорди­нат (см. рис. 4.1). Ось z направим в сторону, противоположную вектору скорости углубки V. Так как схемы вывода уравнений в обоих случаях не отличаются друг от друга, то достаточно рас­смотреть плоскую задачу.

Пусть Гн — достаточно гладкая образующая поверхности определяемая уравнениями 2 = 2(s), r = r(rj), где s — длина дуги, измеряемая вдоль Ги■ По аналогии с теорией пограничного слоя введем нормирование координат s и т] по характерному размеру пенетратора / и толщине слоя расплава б соответственно, т. е. £ = s/l, т] = т]/6. Значения fj = 0 и fj = 1 соответствуют рабочей поверхности пенетратора и поверхности плавления забоя сква­жины. В силу малой толщины слоя расплава геометрия поверх­ностей Ен и 2агр может быть охарактеризована одним и тем же масштабом. Масштабом для составляющих поля скоростей тече­ния расплава в направлении нормали к 2Н будет очевидно слу­жить величина ирт/рж. Масштаб силового взаимодействия (поле давления) характеризуется удельной нагрузкой G; один из темпе­ратурных масштабов задается разностью tarp— too, где too — невоз­мущенная температура твердой среды в бесконечно удаленных точках. Перечисленные выше четыре масштаба имеют независимые размерности в рамках рассматриваемой задачи и являются ее определяющими параметрами. Остальные параметры задачи при­ведут к появлению безразмерных критериев и комплексов подобия.

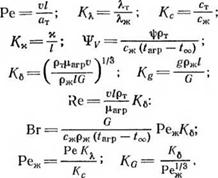
(4.7)

Предварительные исследования общих уравнений (4.1) с по­мощью методов теории подобия и анализа размерностей позволили определить следующие безразмерные характеристики явлений теп — ломассопереноса в жидкой и твердой фазах среды [65]:

где а — коэффициент температуропроводности; к — радиус кри­визны образующей Гн; ц — динамический коэффициент вязкости; g— ускорение свободного падения.

Каждый из критериев и комплексов подобия (4.7) имеет вполне определенный физический смысл, так что сопоставление порядка их величин позволяет выявить основные особенности кон­кретного процесса контактного плавления и обосновать упрощение общей математической модели. Так, для бурения плавлением сква­жин в ледниковых массивах типичны следующие значения пара­метров: безразмерная скорость (критерий Пекле) Ре= 10-^100, Кг. ~ 1, Кс ~ 1, критерий фазового перехода /Сагр — 3 Ч — 100. Для всех практически важных случаев бурения комплекс КЁ, пред­ставляющий собой отношение масштаба толщины слоя расплава к характерному размеру рабочей части нагревателя, в силу малой вязкости воды имеет порядок 10“3, как и комплекс Kg, учитываю­щий влияние массовых сил тяжести в слое расплава; число Рей­нольдса Re меняется в довольно широком диапазоне, но не пре­вышает величины порядка 10~3; число Бринкмана Вг, определяю­щее интенсивность диссипативного разогрева, достаточно мало (10~4—10-5) и поэтому практически не влияет на процессы пере­носа тепла в жидкой фазе. Для относительно гладких участков образующей Г„ безразмерная кривизна Кх — 0.

После соответствующих преобразований и сокращений осред — ненные по толщине слоя расплава безразмерные уравнения со­хранения массы, количества движения и энергии будут иметь вид

TOC o "1-5" h z Я — jg [й* ( V (S. 5j) rtj] _ ■^+ к. Л — §; (4.8)

Д2ЙР — ддтпп = 0; (4.9)

aS дг |т)=1 * дк m

"Реж -4- RvA U(S, л)©ж(5, fj)dti =QH — Qarp, (4.10)

где

п — _£«_ • р — •

Г Нагр ’ о ‘

..,0 И’Рж ^ ^ <н, ж— <агр ^ <7н, агр I

и ч; — врт Де; «н, ж — ,агр _ /оо ; ун, агР — Хж (,агр _ 0.

(4.11)

Я = Ян (5); Z — ZИ(S)—нормальные уравнения кривой Гн; V — параметр (г = 0 для плоской и V = 1 для осесимметричной за­дачи).

При расчете процесса плавления твердой среды кусочно-глад­кой рабочей поверхностью нагревательного устройства 2И урав­нения (4.8) — (4.10) должны быть дополнены специальными усло­виями сопряжения, справедливыми в окрестности угловых точек образующей Гн, где Кк-*~ оо.

В работе [59] показано, что плотность теплового потока Qu на 2Н с точностью до малых слагаемых порядка 0(/С^ — /Се), где /С^==Ян/Яж, определяется решением отдельной задачи о темпера­турном режиме нагревательного устройства, когда на его рабочей поверхности приближенно задано 0 — 0. В связи с этим в даль­нейшем распределение QH будем считать известным.

Выражение для плотности теплового потока Qa, P на поверх­ности плавления 2агР определяется соотношением типа условия Стефана

Qarp = КкОт + Рвж^Сагр + КЬ ^ Ц) , (4.12)

где

Qt= X и q~~t Т (4ЛЗ>

Лт Uarp • оо/

— приведенная плотность теплового потока, поступающего в твердую фазу среды.

Величина QT является одной из основных, характеризующих процесс контактного плавления, и ее расчет основан на анализе задачи, которая аналогична классической задаче теории сварки

о температурном поле 0Т(М) в твердой фазе вокруг сварочной ванны [65]

Д0Т — Ре Щ*- = 0; MgQ; (4.14)

(Д — оператор)

с граничными условиями

©т| =0; 02 =0,; агр 1

Иш ©т = 0,

где ©1 — распределение температуры на поверхности Si проплав­ленной зоны (см. рис. 4.1); 0т = (^т — foo)/(^arp — too) — распреде­ление температуры на поверхности твердой фазы.

Решение задачи (4.14) методом граничных интегральных урав­нений и оценка влияния граничных условий (температурного поля ©1 на поверхности 2i) на плотность теплового потока фт, посту­пающего в твердую фазу с поверхности плавления 2агр, позво­лили существенно упростить интегральное уравнение для QT и по­лучить его в виде [65]

J QT (М)ехр [у Ре (ZD — Z)] ф (М, М0) йГггр = 1; М0 е Гагр,

(4.15)

где Агр — образующая поверхности плавления; ядро ф(Л4, М0) определяется следующими соотношениями: е декартовой системе координат на плоскости

Ф (М, М0) = 2^/С0 [~ Ре — У (Я “ Яо)2 + (2 — 20)2 ] (4.16)

(здесь К. о(х)—модифицированная функция Бесселя втЬрого рода

нулевого порядка);

при наличии осевой симметрии в цилиндрической системе ко­ординат

ь

тл лл К Г ехр(—Ре//2) сИ..

Ф (М, М0) — л ^ ^ _ а2); (4.17)

а

а (М, М0) = У(/?-Я0)2 + (2 — г0)2; ь(м, м0) = ^(я + Яо)2 + (г-г0)2.

Так как при кольцевой форме коронки ось симметрии не пере­секает образующую Гагр поверхности плавления, в уравнениях

(4.15) —(4.17) разность Ь — а —И, где Ю — отношение диаметра керна ак к радиальной ширине торца коронкн /. Тогда при Ре Л

1 для ядра (4.17) может быть построено равномерно пригодное асимптотическое разложение, главный член которого отличается от ядра (4.16) множителем — у/И/Но, а следующий имеет порядок •0(Р е_1£~‘)- Это существенно упрощает расчеты процессов кон­тактного плавления кольцевыми нагревательными устройствами и показывает физически очевидную эквивалентность постановок соответствующих математических задач в плоской декартовой и цилиндрической системах координат при Ре О 3> 1.

Уравнения (4.8) —(4.10) и (4.12) являются основой для по­строения замкнутых, упрощенных для условий /(6<С 1 и Ре ^ 1 математических моделей процессов контактного бурения плавле­нием скважин в снежно-фирновых и ледовых толщах.

Для построения и анализа конкретной математической модели процесса бурения плавлением зададим профили температуры и продольной составляющей скорости течения расплава в зазоре между рабочей поверхностью нагревательного устройства и по­верхностью плавления в виде квадратичных полииоминальных ап­проксимаций по г}. Введем в рассмотрение средние значения тем­пературы ©*(5) и продольной скорости £/д(5) жидкой фазы. Учи­тывая очевидные краевые условия на 2Н при г] = 0 и 2агр при ^=1 и подставляя заданное выражение для (7(5,^) в уравне­нии (4.8) и (4.9) с относительной погрешностью Кб = 0, получаем

Предполагая, что в районе концов образующей рабочей по­верхности (5 = 5] и 5 = 52) поддерживаются заданные значения давления Р(51,)=/31 и Р(52)=Р2, находим постоянную интегри­рования

/гГ’=Гр,-р, + | <4-20>

которую, если е [/?н(52), Рн(-$1)], можно интерпретировать как координату точки разветвления потока расплава, где £?(£) = 0.

В том случае, когда нагревательное устройство является те­лом вращения, а ось г (ось вращения) пересекает поверхность 2Н, условие Р(52) = Р2 не имеет смысла. В этом случае в силу предполагаемой осевой симметрии процесса плавления 5* = 52 и удобно положить 52 = 0. С учетом квадратичной аппроксимации по т| температурного профиля в слое расплава из условия (4.4) определим

г I двж 76„ 1О0Ж / л о!

= ———— Щд— • <4-21>

Тогда уравнения (4.10) и (4.12) принимают вид

Ре. К/г:-‘ — ‘) еж] = 5 (*+0 ; (4.22)

Ре. [«»-§ Ц + ^т] + кл = ~ ■ (4.23)

я,

Уравнения (4.22) и (4.23) вырождаются в тех точках 5, где Р„(5) = Р*(5*) и с№„/(15 = 0 соответственно. Это в свою очередь требует ограничения производных (/©ж/^5 и с/ЛД/5, что позволяет сформулировать необходимые для решения этих уравнений гра­ничные условия. Кроме того, необходимо учесть, что осевая на­грузка, приложенная со стороны рабочей поверхности нагрева­тельного устройства к слою расплава, уравновешивается силами внутренних напряжений в жидкой фазе, которые с точностью до слагаемых порядка /С6 = 0 представлены силами давления. Таким образом, с учетом выражения (4.19) дополнительное условие, ха­рактеризующее равенство внешней силы и результирующей силы реакции со стороны слоя расплава при установившемся процессе бурения плавлением, будет представлено интегральным соотно­шением [65]

о

1 + V

Яг

+ (Р] — 1) Рн (5)) — (Р2 — 1) = 0. (4.24)

Итак, получена замкнутая система уравнений, состоящая из ин­тегрального уравнения (4.15) с равенствами (4.16) и (4.17), двух дифференциальных уравнений (4.22) и (4.23), интегрального

соотношения (4.24), которая позволяет при заданной форме рабо­чей поверхности нагревательного устройства с достаточной для практических целей точностью рассчитать все основные величины, характеризующие процесс бурения плавлением: распределение температуры 0Н(5) или теплового потока Qh(S) на рабочей по­верхности нагревательного устройства, скорость бурения плавле­нием Ре, толщину слоя расплава Д (S), его температуру 0 (S), а затем по формулам (4.18) и (4.19) рассчитать скорость течения расплава U*(S) и давление P(S). Нетрудно видеть, что для про­ведения расчета при помощи сформулированных соотношений не­обходимо дополнительно задать распределение температуры 0Н(5) или, что то же самое в силу равенства (4.21), распределение теп­лового потока Qh(S). Приведенная тепловая мощность, снимае­мая с рабочей поверхности нагревательного устройства, опреде­ляется выражением

s,

NH = 2n J R„QH(S)dS. (4.25)

s2

Образующая поверхности плавления Гатр при условии глад­кости может быть задана параметрическими уравнениями

R = Яагр (5) = RH (S) + к6д (S) dZJdS; (4.26)

2 = Zarp (S) = ZH (S) — K6A (S) dRJdS. (4.27)

Следовательно, в случае устойчивости решения QT уравнения

(4.15) по отношению к небольшим возмущениям поверхности плав­ления возможно в первом приближении с ожидаемой погреш­ностью = 0 заменить кривую интегрирования Гагр в интервале

(4.15) на Ги и реализовать итерационный алгоритм построения решения системы (4.15), (4.22) — (4.24). В результате проблема исследования и решения уравнения (4.15) приобретает самостоя­тельное значение.

Для практически важного частного случая, когда образующая поверхности плавления Гагр есть парабола Zarp== A(Rarp— /?*)2 с параметром удлиненности А > 0, на основании анализа задачи

(4.14) получено решение уравнения (4.15) в виде

Pegp(-g’) /Г УясагИа). v = 0;

Vl + 4AZarp ‘ I а E1 (—a ), V=l,

где

со

а2 = —; erfc (а) = —р=- ехр (—и2) du;

4 А Л/Я J

* а

со

Ei (а) = $ .«Ф.(-«») (1и

1

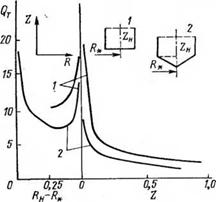
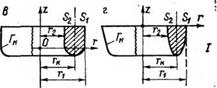
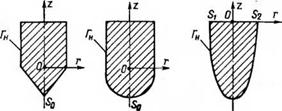
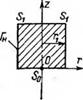
Для расчета процессов контактного плавления при произволь­ных формах рабочей поверхности нагревательных устройств в ра­боте [65] был предложен алгоритм численного решения уравне­ния (4.15), основанный на методе Крылова — Боголюбова, с по­мощью которого проведено несколько серий вычислений на ЭВМ. В процессе этих расчетов проанализированы четыре основные формы сечений рабочей поверхности нагревательных устройств, наиболее часто используемые при бурении скважин в ледовых толщах (рис. 4.2):

а) квадратная — f(R„) = 0; ZH=1, где ZH — безразмерная вы­сота вертикальной составляющей;

б) треугольная — /(#„) = |/?н — Я* | — 0,5; ZH = 0,75;

в) полукруглая — / (/?„) = Уо,25 _ (#н _ Zn = l _ 0,125я;

г) параболическая — /(/?„) = А [(/?„ — RJ2 — 0,25]; ZH = 0; Л==6.

При расчетах были использованы следующие значения физи­ческих величин, входящих в безразмерные параметры и комп­лексы: taгр — too = 50 °С; / = 0,02 м; г* = 0,065 м; т]з = 335 кДж/кг; ст = 2,1 кДж/(кг-°С); сж = 4,2 кДж/(кг-°С); |лагр = 1,8-Ю“3 Па-с; ^ж = 0,6 Вт/(м-0С); Кт~ 2,5 Вт/(м-°С); рж = 990 кг/м3; рт = = 920 кг/м3; G = 61,2 кПа; ui = 2,8-10~4 м/с (1 м/ч); v2 = = 8,3-10~4 м/с (3 м/ч); v3 = 1,67-10-3 м/с (6 м/ч).

Результаты вычисления распределений QT для вышеперечис­ленных типов поверхностей плавления представлены на рис. 4.3. Нетрудно видеть, что наличие угловых точек на образующей ра­бочей поверхности нагревательного устройства Гн будет приво­дить при малых значениях К& к аномальному увеличению плот­ности теплового потока Qr в их окрестностях, к нерациональному перегреву слоя расплава в промежуточных областях и, как след­ствие, к снижению эффективности работы устройства.

Оптимальная форма рабочей поверхности теплового пенетра- тора может быть найдена только при рассмотрении процессов тепломассопереноса в слое расплава и рассеивания тепла в окру­жающий забой твердый массив. Для сопоставления различных кон­струкций нагревательных устройств введем в качестве меры эф­фективности их формы и конструкции коэффициент полезного дей­ствия р, который определим как отношение тепловой мощности N0, минимально необходимой для проплавления твердой среды в миделевом сечении нагревательного устройства, к мощности NH, снимаемой с его рабочей поверхности (4.25):

P = W, (4.29)

где

N0 = л Rl (SO — Rl (s2)l (Ко ~ Karp) Реж.

Расчеты, выполненные на основе построенной выше матема­тической модели процесса контактного бурения плавлением (4.15) и (4.24) при фиксированном объеме нагревательного устройства, т. е. при одной и той же тепловой мощности, показали, что при прочих равных условиях максимальные значения КПД соответ­ствовали тепловым пенетраторам с параболической формой рабо­чей поверхности [39, 65].

I

Гн

__ a

S2 S, “Я

Гк

У/

Гк

ч

Рис. 4.2. Формы осевых сечений забойных нагревательных устройств. I—кольцевые; II—сплошные: а — квадратная, б—треугольная, в—полукруглая, г—параболи-

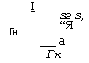Рис. 4.3. Распределение плотности теплового потока QT, поступающего в ледя­ной массив с поверхности плавления при Ре =15, для цилиндрических нагрева­тельных устройств с плоским (/), коническим (2), полусферическим (3) и пара- болоидным (4) торцами.

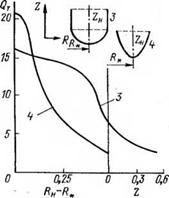Наиболее наглядно анализ влияния формы рабочей поверх­ности нагревательного устройства на эффективность процесса бу­рения плавлением может быть проведен на примере часто реа­лизующейся в практике конструкции пенетраторов с изотерми­ческой рабочей поверхностью. Так как в рамках рассматриваемой математической модели в силу соотношения (4.21) задание рас­пределения температуры 0Н на Ен равносильно заданию распреде­ления плотности теплового потока Q„, то при Q = const, т. е. для нагревательного устройства с изотермической рабочей поверх­ностью, хотя бы приближенно, должно выполняться условие

QH/(dRjdS) = В = cont. (4.30)

В этом случае решение системы уравнений, представляющей собой математическую модель процесса бурения плавлением, зна­чительно упрощается и может быть найдено в явном виде [65]:

дЗ __________________ 6р + Й)________________

(V + 1) К (5.) (1 — Р.) — % (Я2) (1 — р2)] ^

х 5 (яг1 (-§1)3^ (4-з1>

я,

0„ = Реж/(6ВА(1 + 0,1 Реж К<£)/( 1 — 0,15 Ре*ДвД); (4.32)

<2„ = Р ежЯ (1 + 0,35 Реж ед/( 1 — 0,15 Реж /СвД); (4.33)

©ж = 0,5 Реж/С6ВД/(1 — 0,15 Реж/С6Д), (4.34)

где Д = Д йЯ/йБ; фн — С}И

В = Чу + ВКк.

Формулы (4.31) — (4.34) удобны для проведения оценочных ин­женерных расчетов.

Анализ влияния удлиненности нагревательного устройства (теп­лового пенетратора) параболической формы, характеризующейся параметром А, на эффективность процесса контактного плавления, т. е. на коэффициент полезного действия р, показывает, что с уве­личением параметра А уменьшается толщина слоя расплава, сни­жается его температура и, следовательно, снижаются потери, свя­занные с непроизводительным перегревом слоя расплава. Однако при этом возрастают потери тепла в твердой фазе. Следовательно, оптимальная форма рабочей поверхности нагревательного устрой­ства может быть найдена при совместном рассмотрении процес­сов тепломассопереноса в слое расплава и рассеивания тепла в •окружающий нагревательное устройство ледяной массив.

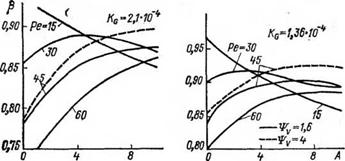
На рис. 4.4 приведены расчетные зависимости коэффициента полезного действия (3 от параметра удлиненности кольцевого пе­нетратора А для процесса контактного плавления в ледяном мас­сиве с различными скоростями (Ре равно 15, 30, 45 и 60). Все не­обходимые для расчетов данные приведены выше. Кривые, изо­браженные сплошными линиями, соответствуют значению Ч’у = 1,6 при £агр — ^<х, = 50оС, а изображенные штриховыми линиями — значению Ч’у = 4 при ^агр — £» = 20 °С.

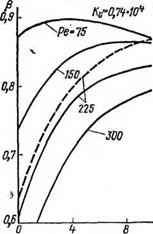
Аналогичные расчеты при тех же теплофизических свойствах льда, удельных нагрузках на забой и скоростях плавления про­ведены для сплошных нагревательных устройств (параболоидов вращения) (рис. 4.5). В последнем случае в качестве характер­ного размера / выбирался максимальный диаметр нагреватель­ного устройства, который был принят равным 0,1 м. В соответ* ствии с этим изменились и зависящие от этого размера безраз­мерные величины Ре и Кс (Ре равно 75, 150, 225 и 300; Кв равно

0, 74-10-4 и 0,46-10-4).

Рис. 4.4. Зависимость коэффициента полезного действия р термобура от удли­ненности А кольцевого нагревательного устройства при плавлении забоя в ле­дяном массиве.

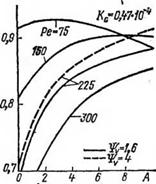Рис. 4.5. Зависимость коэффициента полезного действия р от. удлиненности А нагревательного устройства для сплошного плавления забоя в ледяном массаве.

Анализ полученных расчетных зависимостей Р = ДЛ) под­тверждает справедливость вывода о том, что при высоких скоро­стях контактного плавления (Ре > 45 при кольцевом забое и Ре >• 150 при сплошном) вытянутая форма нагревательного устройства А > 1 является более предпочтительной, особенно при бурении плавлением в умеренных и «теплых» по температурным условиям ледниках, когда разность taгp— невелика и рассеива­ние тепла на прогрев твердой фазы играет второстепенную роль. С другой стороны, при контактном плавлении с небольшой ско­ростью (Ре < 15 для кольцевого забоя и Ре < 50 для сплошного) в низкотемпературных ледниках, наоборот, процессы тепло — и мас — сопереноса в слое талой воды под торцом нагревательного устрой­ства становятся несущественными, а тепловые потери в ледяной массив существенно возрастают. В результате оптимальная форма
рабочей поверхности приближается к плоской (А < 1). В проме­жуточных областях режимов контактного плавления льда при бурении скважин выбор оптимального значения парамётра А ие яв­лялся тривиальным. Однако во всех рассмотренных случаях коэф­фициент р остается достаточно высоким: 0,77 < р С 0,92 для коль­цевых пенетраторов и 0,63 < р < 0,93 для пенетраторов в форме параболоидов вращения при изменении параметра А в интервале 2< А < 10.

Комментарии запрещены.