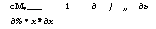Бурение грунтовых зондов, установка энергетических колодцев

Крепление ствола скважины (также и керна) за счет форми­рования на стенках остеклованного слоя расплава достигается тем, что вслед за плавящим рабочим органом бурового снаряда — сплошным или кольцевым высокотемпературным нагревателем — располагается охлаждаемая секция кристаллизатора-формирова­теля, выполненная из жаростойкого, высокотеплопроводного мате­риала, обладающего минимальной адгезией к застывающему расплаву и химически слабо с ним взаимодействующего.

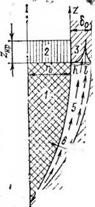
Для обеспечения условий формирования на стенках скважины (керна) в процессе бурения плавлением остеклованного слоя за­данной толщины, контроля и регулирования его характеристик и свойств необходимо исследовать процесс охлаждения и застыва­ния этого слоя. Изучение динамики твердения расплава на стен­ках скважины и керна позволит обосновать выбор оптимальных размеров кристаллизатора-формователя и разработать эффектив­ный режим его охлаждения. С этой целью разработана и исследо­вана математическая модель процесса формирования остеклован­ного слоя на стенке скважины при бурении плавлением, схема которого представлена на рис. 5.4. [69].

Пусть в процессе бурения скважины при проплавлении забоя на некоторую фиксированную углубку выше рабочей теплопере­дающей поверхности нагревательного устройства бурового снаряда образовался слой расплава толщиной бо с температурой, близкой к температуре агрегатного перехода горных пород. Первоначаль­ная температура твердой фазы горных пород на рассматриваемой

Рис. 5.4. Схема процесса формирования стенок сква­жины при бурении плавлением горных пород.

1

У//////

У///’’?//, /// /. *

‘////А ш

— нагревательное устройство; 2— кристаллизатор-формова — тель; 3 — застывший расплав горной породы; 4 — горная поро­да; 5 —расплав.

"04^ У’,/ /у?’/Ц/у’//У’ У/У/////4’////Л

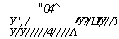глубине была равна Ъо — Далее в процессе прохождения выделенного фиксированного интервала следующей за нагревателем секцией кристаллизатора-формирователя со скоррстью V, равной скорости бурения пла­влением, образующийся расплав будет кон­тактировать с охлаждаемой поверхностью этой секции.

В результате за время т — Н/ь, где Н— высота кристаллизатора-формирователя,

слой расплава твердеет на величину к со стороны бурого снаряда за счет контакта с охлаждаемой поверхностью кристаллизатора- формирователя и на величину I со стороны горного массива за счет отвода в последний от расплава части теплового по­тока.

Очевидно, что процесс формирования остеклованного слоя на стенке скважины завершится, когда

Мтс) + / (тс) = 60, (5.27)

где тс — время смыкания двух фронтов отвердевания расплава на фиксированной глубине.

Определяя из уравнения (5.27) время тс, найдем требуемую длину охлаждаемого участка кристаллизатора-формователя Н = = 1>тс. Выбираем систему ортогональных координат х и г так, как показано на рис. 5.4. Чтобы найти функции 6(т) и 1(т), необхо­димо сформулировать и решить задачу о переносе теплоты в об­ластях хе[0,6], хе[б0—Учитывая, что для всех практи­ческих случаев бурения толщина слоя расплава, выдавливаемого в кольцевой зазор между нагревательным устройством и стенками скважины (керна), значительно меньше характерного размера са­мого нагревательного устройства г0, т. е. бо/го С 1, для опреде­ления температуры твердой фазы в области [0, 6] запишем одно­мерное уравнение теплопроводности

т_ дх2

= О,.

дх

О < х < 6 (т), т > О	(5.28)

TOC o "1-5" h z со следующими начальными и граничными условиями: ^ а) т = 0, 6 = 0;

б) х = 0, =

х < / — д1 , с16

ч в) X О, Г /агр, Ат ^ ^ ,

где ат и к — коэффициенты температуропроводности и теплопро­водности твердой фазы; ґ, ^агр и ^ох — температуры твердой фазы, агрегатного перехода и охлаждающей среды; ■фу — скрытая объ­емная теплота агрегатного перехода; И — коэффициент теплопере­дачи через охлаждаемую стенку.

Введем безразмерные переменные

X	ат т Рп —	; 0:	І ^агр
	62 °0	^агр ^ох
К —	^агр	Ві	Ь&о
Л© —	^агр ^ох	Лт *
тг——-	%		6
^ у —	СтРт (^агр	/о) в	Д=“6Г

где ст и рт — теплоемкость и плотность горной породы в твердом состоянии.

Подставив в систему уравнений (5.28) — (5.29) новые безраз­мерные переменные, получим

ТтгЧЦ — «<*<*> Ро>° (5.30)

с начальными и граничными условиями г а) Ро = 0, А = 0;

б)* = 0, § = ВН0+1); (5 31)

»,* = *. в = 0. § = КеЧу-ЦЬ-

Простое приближенное решение этой задачи получено в ра­боте [69]. Оно имеет вид

е=вгЛ~в? д ’ <5-32>

ЗД2 4- В1 Д3 , Г[Г 2Д + В! Д2 /к

р0 = 6(1+ вГд) + —Щ— ■ (5-33)

Для области ] (бо —/), б0[ с теми же допущениями, что и для первой зоны [0, б], можно записать

: ат -^г, б0 — / х ^ б0,

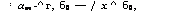д/т ___ д2/т

д% йт дх2

т>0 (5.34)

с начальными и граничными условиями

а) т = 0; I = 0;

В граничных условиях задачи (5.35) поток ^(т) не известен и должен быть определен из решения задачи для температурного поля пород и в области [бо, оо [, которая формулируется в виде

сМт___ 1 д / „ дь д% т х’3 дх

(‘£)•

»о + 60<х < ОО, (5.36)

с начальными и граничными условиями

а) т = 0, /т = /0(х);

б) х = уг0 + во, /т = / (60, т), —Лт (т); (5.37)

в) х > оо} /т — /„-»О,

где /’о — радиус нагревательного устройства; V — параметр (для кольцевого нагревательного устройства V =0, для сплошного

V = 1).

Условия (5.37) служат для определения потока <?(т).

Решение поставленной задачи было подробно рассмотрено в работе [69].

Для бурения скважин плавлением сплошным забоем ^ = 0) получены следующие приближенные выражения для определения безразмерной величины теплового потока к фронту кристаллиза­ции ф(Ро) и безразмерной переменной, характеризующей положе­ние этого фронта кристаллизации

<2 = р/д/я Ро; (5.38)

Ь = 2а ^/¥о; (5.39)

(5.40) (5-41)

+4Р2 — Чут/п _

2(5 ’

где

-2 (1 + ¥,,) + дАі’І’2 + (32/я) ЧГу + 16/» 2 (4/зх — I)

п 60<7 (т) » I

4 ъи-и’ 60 •

Анализ выражения (5.41) показывает, что при значениях Ч’у > 1 р-> 1, тогда выражения (5.38) и (5.40) можно записать в виде

1 л/^ + 4 —

<2 = -7==-; а =—————————————————————— • (5.42)

Уяго 2

Значения параметра а, полученные по формулам (5.40) и (5.42) и р-—по формуле (5!’41), приведены в табл. 5.1.

Данный пример характерен тем, что в начальный момент тем­пература слева от границы х = 6о равна температуре агрегатного перехода /агр, а справа от поверхности л: = бо равна невозмущен-

Таблица 5.1 Значения параметров о и р в зависимости от критерия Параметр Формула 0,05 0,1 0,5 і 5 10 » (5.40) 0,914 0,842 0,519 0,353 0,1 р (5.41) 0,492 0,513 0,630 0,715 0,898 0,943 (5.42) 0,957 0,915 0,651 0,449 0,11 0,056

ной температуре пород /то. Поэтому в первые моменты времени поток при х = б() принимает большие значения, и температура резко меняется. В действительности в момент начала кристалли­зации слоя расплава температура пород непрерывно меняется от (ягр до ^т0. Поэтому резких изменений температуры не будет и поток (} при х = 60 принимает конечное значение. Это позволяет надеяться, что использование формулы (5.38) для расчета вели­чины Ь в реальной ситуации даст значительно более точные ре­зультаты, чем в рассмотренном примере.

В случае бурения кольцевым термобуром (V = 0) температур­ное поле в породе может быть описано зависимостью [65]

Ґ ^ Ре X У~2^ ( л/Ре бо У V 2 Го)

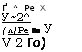
|^х<оо( (5.43)

1,-1. ег’Ч 2 г.

ЄГЇС

где Ре = юхо/ат; х0 — толщина кольца нагревательного устройства.

Для теплового потока ф и границы кристаллизации Ь получены следующие выражения:

>Ркехр{-е7[4(і + /Сае2)1} —

<3 = є, —7 1………. = а , є„ = е УРе, (5.44)

д/(і + Ка Ио є2) я егіс (е»/2)

где е = боДо; в большинстве случаев є» <С 1, следовательно,

<1= (5.45)

_____ і’Ді. .

л](+К0 Ро є2) я

іКІ^/і+КаРо,2-]

п1<а Vі + Ка р0 е! Кке,

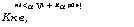^71(1 + Ка^Ое]).

(5.46)

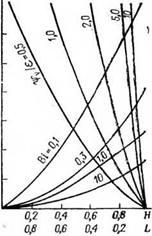
Результаты расчетов по формуле (5.46) для различных значе­ний Чгу и е приведены в табл. 5.2 и на рис. 5.5.

Так как е* — С 1, то формула (5.46) может быть значительно упрощена. Действительно, максимально возможное значение па-

Расчетная зависимость фронта кристаллизации Ь от безразмерного времени Ро при различных значениях Чгу/г для условий К^ = Ка — Кв= 1 Fo «V =0,1 Vy = l, е = 0,1 е=0,1 е=0,01 0 0 0 0 0,2 0,109 0,11 0,01 0,4 0,213 0,022 0,022 0,6 0,311 0,034 0,034 0,8 0,404 0,045 0,045 1,0 0,494 0,056 0,056 1,2 0,580 0,068 0,067 1,4 0,744 0,09 0,078 1,6 0,744 0,09 0,09 1,8 0,822 0,101 0,112 2,0 0,898 0,112 0,112 2,2 0,97 0,12 0,12

W

Рис. 5.5. Зависимость безраз­мерных фронтов кристаллиза­ции Н и /, от безразмерного времени Ро для различных зна­чений критериев Ч’У/е и В! при Кв = К = Ка = 1 * Кагр ~ 0*1*

раметра Фурье Fo имеет порядок 4V/e*, так как L <С 1, следова­тельно, 1+ATaFoef« 1 при 4V = 0(1).

Тогда выражение (5.46) примет вид

4V /7 Vit V /г

‘• = —fcr+VHsr) +2F°- <5’47»

Очевидно, что проекция точки пересечения кривых Н = Н(Fo)

и L = L(Fo) на ось Fo (см. рис. 5.7) дает решение уравнения

(5.27) , т. е. позволяет определить относительное время форми­рования остеклованного слоя Foc. Затем по формуле

ZKp = ePeFoc, (5.48|

где Zkp — требуемый относительный размер для охлаждаемой зоны, Foc — найденное решение уравнения (5.27), вычислим необходи­мый размер охлаждаемого участка

^кр ZKp/(i, (5.49)

где /о = Л0 + 00-

Аналогичные рассуждения можно привести для случая v = V. Заметим, что, так как е мало, a Fo имеет порядок 4V/e, при 4V = 0(1) тепловой поток Q практически не меняется и равен своему начальному значению Q = е, Дя/Уя. Очевидно, что подоб­ная картина будет наблюдаться и прй v = l. Таким образом.

учитывая, что температурное поле в породе может быть представ­лено в виде выражения [40]

11 /гЛ_ Ei[- (Ре/4) (/-„’//„+е* + е)] ______________ /г rm

и^)~- ЕИ-(Ре/4)(г0//0 + е)] ■ (5.50)

оо

где Ei (sim) = ^ —— ■■■“- du; r0 — радиус кристаллизатора-формо — вателя, получаем

2еКк exp(-Ped2/4) j _ „ ,г с.

Q — d ■-Ei(-Ped2/4) ’ d = r°llo — (5.51)

Зная Q, по формуле (5.39) найдем L и определим время пол­ного застывания (кристаллизации) расплава на стенке скважины, которое при заданной скорости бурения плавлением позволит нам рассчитать высоту охлаждаемого участка кристаллизатора-форми­рователя или при заданной высоте определить условия его охлаж­дения: температуру охлаждающей среды tt>x и коэффициент теп­лопередачи k.

Комментарии запрещены.