Бурение грунтовых зондов, установка энергетических колодцев

Процессы тепло — и массопереноса, происходящие в скважине при бурении, разнообразны и подвержены влиянию большого ко­личества разнородных по своему действию факторов. Их прогно­зирование и нормализация являются весьма сложной задачей, для решения которой целесообразно привлечение методов моделиро­вания [5, 11, 23, 31, 45].

В самом общем виде модель есть искусственно создаваемый объект исследования, отражающий свойства, характеристики и связи оригинала, существенные для решения поставленной задачи. Модель отражает действительные свойства и состояние объекта — оригинала только приближенно, в некоторой области характери­зующих его параметров и, как правило, намного проще оригинала. В соответствии с формой представления все модели можно раз­делить на идеальные или теоретические и материальные или экс­периментальные.

В общем случае теоретическая модель — это система матема­тических соотношений, которая отражает наиболее существенные свойства реального объекта или устанавливает взаимосвязи ме­жду определяющими параметрами исследуемого процесса.

Моделирование на прикладном уровне заключается в первую очередь в выборе для описания заданного процесса достаточно об­щей «стандартной» модели, схематизацию геометрических форм и квалификацию тел в качестве материальных точек, абсолютно твердых и деформируемых сред с теми или иными реологическими свойствами. Взаимодействие тел учитывается понятием силы. «Стандартные» . математические модели используют универсаль­ные физические законы (сохранения массы, движения, энергии, второй закон Ньютона и т. п.). Для составления систем уравне­ний часто применяют хорошо обоснованные полуэмпирические и чисто эмпирические соотношения. При выборе законов или гипо­тез, полагаемых в основу модели, нужно останавливаться на са­мых простых, которые легко подтвердить или опровергнуть экспе­риментально.

Тепловые явления характеризуются процессами теплопереноса, которые часто сопровождаются переносом вещества (при агрегат­ных превращениях, диффузии и пр.), называемым массообменом. В этих случаях имеет место сложный процесс тепло — и массопере­носа или тепло — и массообмена.

Основой математического описания явлений тепло — и массо­переноса являются законы сохранения массы, импульса и энергии, к которым для конкретных условий присоединяются дополнитель-

ные соотношения связи между параметрами среды и процесса. Эти законы и соотношения формулируются в виде системы диф­ференциальных уравнений. Для описания конкретного процесса к системе дифференциальных уравнений добавляются краевые условия или условия однозначности.

При анализе происходящих в бурящейся скважине процессов она рассматривается как тёплообменная система с изменяющи­мися по глубине и во времени условиями и параметрами. Опреде­ляющими являются конструкция скважины, технология бурения, и прежде всего способ очистки забоя от продуктов разрушения по­роды: качество и расход очистного агента как холодо — или тепло­носителя, схема и характер циркуляции. Обычно приходится иметь дело с течением жидких, газообразных и газожидкостных промы­вочных агентов в цилиндрических каналах колонн бурильных и об­садных труб, в кольцевых каналах между бурильными и обсад­ными трубами и стенками скважины, а также в каналах трубо­проводов и соединительных шлангов поверхностной обвязки. В циркуляционной системе скважины встречаются различные ме­стные сопротивления (сужения и расширения сечений, изгибы, повороты и т. д.).

Анализ гидравлических и связанных с ними тепловых процес­сов существенно облегчается, если циркуляционную систему сква­жины разделить на четыре характерные и относительно самостоя­тельные части (рис. 1.12).

I. 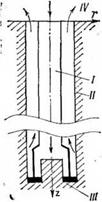Ствол скважины, заполненный в процессе бурения промы­вочной средой, обеспечивающей очистку забоя и вынос продуктов разрушения породы, а также устойчивость стенок скважины. При механическом способе бурения эта часть состоит из связанных между собой двух зон. Первая представляет собой внутренний ка­нал бурильных или обсадных труб, через который происходит по­дача промывочной среды в зону забоя в процессе бурения или продавливание тампонажного раствора в затрубное пространство в процессе цементирования, вторая — кольцевой канал между ко­лонной бурильных труб и стенками скважины или обсадными тру­бами. Тепло — и массообмен в этой зоне опреде­ляется интенсивностью циркуляции среды, ее взаимодействием с окружающим скважину гор­ным массивом, в том числе с пластовыми жид­костями и газами. При цементации тепло — и массообмен определяется характером и вре­менем вытеснения одного раствора другим, а также условиями формирования цементного камня.

И. Массив окружающих скважину горных пород, характеризующийся определенными

Рис. 1.12. Схема для анализа процессов тепломассопере — носа при бурении скважины.

физическими и тепловыми свойствами, процессами тепло — и массо — переноса и др.

III. Зона забоя скважины, где происходит разрушение горной породы, образующийся буровой шлам выносится потоком промы­вочной среды, которая участвует в теплообмене с породоразру­шающим инструментом, породой забоя и буровым шламом. Для передачи энергии породоразрушающему инструменту вблизи этой зоны может быть размещен забойный двигатель или другой пре­образователь энергии.

IV. Поверхностная обвязка устья скважины, включающая в себя емкости и устройства, где происходят очистка, об­работка и приготовление промывочной среды и тампонажных рас­творов.

При бурении характер протекающих в скважине гидравличе­ских и тепловых процессов часто меняется, но может считаться относительно установившимся для следующих основных техноло­гических процессов.

1. Нормальное бурение (углубка) скважины без существен­ных геологических и технологических нарушений, когда в зоне забоя при работе породоразрушающего инструмента выделяется теплота, а циркуляция промывочной среды в системе происходит по схеме «противотока».

2. Промывка скважины, когда циркуляция промывочной среды происходит без углубки скважины, т. е. без разрушения породы забоя.

3. Спуско-подъемные операции, связанные с необходимостью извлечения керна или замены бурового инструмента, когда от­сутствуют процесс разрушения породы забоя и циркуляция про­мывочной среды, теплообменные процессы происходят между за­полняющей скважину средой и массивом горных пород.

4. Цементирование обсадной колонны и создание вокруг нее оболочки из цементного камня. Одна жидкость вытесняется дру­гой, тепло — и массообменные процессы определяются динамикой и теплофизическими свойствами этих жидкостей, физико-химиче­скими процессами образования цементного камня и влиянием ок­ружающих горных пород.

Тепло — и массообмен во всех частях рассматриваемой области взаимосвязан, однако для конкретных технологических операций определяющими становятся процессы, происходящие в какой-ни­будь одной или двух из четырех частей. Например, температур­ный режим бурящейся скважины определяется в основном тепло­обменными процессами в стволе скважины и в окружающем его горном массиве, а влияние призабойной и поверхностной частей исследуемой области может быть учтено условиями на границах. При изучении температурного режима породоразрушающего ин­струмента или процессов разрушения горных пород нетрадицион­ными способами возникает необходимость исследования тепломас­сообмена в призабойной части скважины, а влияние остальных частей области можно отразить в граничных условиях.

Изучение процессов тепло — и массопереноса в бурящейся сква­жине начнем с рассмотрения задачи о распределении температуры вдоль оси скважины во встречных потоках промывочной среды, т. е. задачи о температурном режиме бурящейся скважины. Эта задача крайне сложна, так как распределение температуры в стволе скважины зависит от большого числа факторов: конструк­ции скважины, геометрических характеристик колонн обсадных и бурильных труб, физических и теплофизических свойств промы­вочной среды, металла, цементного камня и окружающих горных пород; режима течения и реологических характеристик бурового раствора, его расхода; распределения температуры в массиве гор­ных пород; наличия местных источников тепла; длительности циркуляции и ее перерывов и т. д. Кроме того, значения целого ряда характеристик и параметров сами по себе зависят от тем­пературы, а граничные и начальные условия не всегда легко и просто сформулировать. Поэтому в качестве исходной и наиболее общей рассмотрим следующую задачу.

Пусть в скважину радиусом jR0 опущена колонна бурильных труб с радиусом внутреннего канала г, через которую нагнетается промывочная среда с массовым расходом G и начальной темпе­ратурой ti„. В процессе бурения поток промывочной среды в бу­рильной колонне по мере приближения к забою изменяет свою температуру, которая всегда остается отличной от температуры окружающей среды. В области забоя за счет теплоты, выделяемой при работе породоразрушающего инструмента, промывочная среда претерпевает местный нагрев на величину At3. Изменив в зоне забоя направление на противоположное, промывочная среда по затрубному кольцевому каналу устремляется к устью скважины (см. рис. 1.12). Восходящий поток промывочной среды в кольце­вом канале находится в тепловом взаимодействии с массивом гор­ных пород и с нисходящим потоком. Кроме того, промывочная среда воспринимает теплоту, в которую превращается практи­чески вся энергия, необходимая на преодоление гидравлических сопротивлений и на вращение бурового инструмента — в скважине.

Требуется определить температурные поля во внутреннем ка­нале колонны бурильных труб, в кольцевом канале и в окружаю­щем скважину массиве горных пород.

Рассмотрим связь между движением промывочной среды и теп­лопередачей в отдельных частях исследуемой области. Процессы передачи теплоты и движения среды неразрывно связаны друг с другом. Состояние потока промывочной среды (жидкости или газа) можно считать определенным, если известны пять его основ­ных гидродинамических характеристик: давление р, температура t и три компонента вектора скорости v, т. е. известны зависимости

Р — Р (х, у, г, т);

t = t {х, у, z, т); (1.14)

v = v (х, у, z, т),

где х, у и г — декартовы координаты;, г — время.

Теоретическое изучение теплообмена и движения промывочной среды сводится к отысканию соотношений (1.14). Для определе­ния пяти неизвестных целесообразно вывести систему из не менее чем пяти общих уравнений, которыми в гидродинамике являются соотношения, выражающие законы сохранения массы, импульса (количества движения) и энергии.

Дополнительные уравнения, связывающие физические свойства среды и внутреннюю энергию с давлением и температурой (тер­модинамические уравнения состояния и реологические соотноше­ния) позволяют составить замкнутую систему, описывающую про­цесс конвективного тепломассопереноса. Решение такой системы уравнений в сочетании с граничными и начальными условиями позволяет в общем решить поставленную задачу и определить зависимости (1.14) в любой точке и в любой момент времени.

Если обозначить концентрацию субстанции (массы, импульса, энергии) через с, мощность источников или стоков субстанции — через 1, удельный диффузионный поток субстанции — через /.урав­нение, выражающее закон сохранения субстанции, запишется в виде

^ЛС<дЛ = — фа-п)^+$ЫК. (1.15)

ЧК / 5 V

Здесь й/йх — полная производная по времени; V — выделен­ный объем; 5 — поверхность, ограничивающая объем; п — нор­маль к поверхности 5.

Применив к уравнению (1.15) формулу Лейбница и теорему Остроградского — Гаусса, нетрудно получить дифференциальное уравнение переноса субстанции

-^=-с11у(] + Су) + /, (1.16)

где

<ЭА дАи дк ШуА * 1

дх ‘ ду дг

Из уравнения (1.16), в частности, следует, что поток субстан­ции определяется диффузионным переносом и видимым движе­нием среды (конвективным переносом).

Для простоты будем считать, что циркуляционный агент в скважине является однородной средой, в которой отсутствует пе­ренос теплоты излучением. Если теперь принять, что переносимой субстанцией является масса, то, очевидно, имеем с — р, ]=/ = 0, и уравнение (1.16) принимает вид

др/дх + сНуру = 0. (1.17)

Здесь р — плотность среды.

Уравнение (1.17) называется дифференциальным уравнением сохранения массы или уравнением неразрывности.

Пусть переносимой субстанцией является количество движе­ния, тогда с — рх, а так как диффузионный поток импульса обусловлен тензором давления Р, то $ = Р. Известно, что тензор Р раскладывается на сумму двух тензоров:

Р = /р + а,

где р — гидростатическое давление;

100′

/=I 010

.001

• единичныи тензор;

{

&хх сху °хг "J

°ух °уу °уг Г

®zx &zy &zz >

— тензор вязких напряжений.

Внутренним источником движения является суммарное дей­ствие всех массовых сил (гравитационные и др.) Fk

/ = ZpKFft.

Подставляя в уравнение (1.16) соответствующие выражения для с, / и J, после преобразований получаем

р dv/dx ——Vp— div cr — f — 2pKFK. (1.18)

Это уравнение называется уравнением сохранения импульса или уравнением движения. Оно выражает тот факт, что полное уско­рение потока равно сумме градиента давления, изменения ско­рости за счет сил внутреннего трения и действия всех массовых сил. В частном случае, когда поле массовых сил сводится к гра­витационному, уравнение движения можно записать в виде

р dv/dx — —Vp — div о — f — pg. (1.18a)

Здесь dv/dx = dv/dx + (v • V); V = grad = (д/дх, d/dy, d/dz)’ (v • V) — скалярное произведение векторов, div a — dajdx + + dojdy + dajdz — ax = (axx, axy), axz; ay = (ayx, ayyr oyz) oz = (огх,

&zyi ®zz)-

В том случае, когда переносимой субстанцией является энергия,

с — ри + (1/2) pv2, (1.19)

где pw — потенциальная энергия, (1/2)ри2— кинетическая энергия.

Диффузионный поток энергии для однородной однокомпонент — ной системы равен потоку тепла q, т. е. j = q. Источниками энер­гии являются работа всех сил и объемное выделение теплоты ре. В рассматриваемом случае работа производится силой тяжести, а также силами давления и внутреннего трения, которые характе­ризуются тензором давления Р. Следовательно, в выделенном объеме V источники энергии будут равны

^ / dV = $ (pvg) dV — § (vP) n dS + ^ pe dV

V V S V

или, применяя теорему Остроградского—Гаусса, получаем

^ / dV = ^ (pvg) dV — ^ div (vP) dV + ^ pe dV.

V V V V

Отсюда

J = (pvg) — div (vP) + pe.

Подставив полученные выражения в уравнение (1.16), найдем зависимость, характеризующую перенос энергии

(д/дх) (pt> + ~ ри2) + div [(ри + у ри2) и] +

+ div g = (pvg) — div(vP) + pe. (1.20)

Первый член в левой части полученного уравнения характе­ризует локальное изменение энергии в единицу времени, второй член— конвективный перенос энергии со скоростью текущей среды и третий член — диффузионный поток энергии. Правая часть урав­нения состоит из суммы трех источников энергии: работы сил тя­жести, работы сил давления и внутреннего трения и объемного выделения теплоты.

Уравнению (1.20) можно придать иную форму, записав его как уравнение переноса энтальпии h — v — f — P/p:

p dh/dx = — div q + dP/dx — [(a*V) v] + pe. (1.20a)

Здесь

[(o*V) v] = (ax dxjdx) + (cy dxjdy) + (az dv/dz).

Получение трех уравнений недостаточно для полного описания явлений тепломассопереноса, так как число искомых переменных превышает число уравнений. Действительно, к членам уравнений (1.14) добавились плотность, компоненты тензора напряжений и поток тепла q. В качестве недостающих уравнений воспользуемся так называемыми феноменологическими законами, устанавливаю­щими связь перечисленных выше параметров со скоростью потока, давлением и температурой. Так, например, уравнение состояния связывает плотность среды с давлением и температурой. Вид этой связи зависит от вида рассматриваемой жидкости или газа. Про­стейшей структурой обладает уравнение для несжимаемой жид­кости

р = const. (1.21)

Весьма употребительна баротропная форма уравнения состоя­ния— Р = р(,р). В случае реального газа можно воспользоваться уравнением Клайперона-—Менделеева, широко применяемым для зон, удаленных от критической области движения:

Р/Р — ZRT. (1.22)

Здесь Т—абсолютная температура, К; R = (R/M)g Я — уни­версальная газовая постоянная (Я! = 843 моль/К); М — молеку­лярная масса; g — ускорение свободного падения; Z — коэффи­циент сжимаемости, характеризующий отклонение реального газа от идеального.

Зависимость вектора теплового потока ч от температуры уста­навливается законом Фурье, согласно которому

ч = —т, (1.23)

где / — температура, °С; К—коэффициент теплопроводности, за­висящий от свойств рассматриваемой среды.

Течение представляет собой один из видов деформации, кото­рая очевидно связана с возникшими в среде напряжениями, ха­рактеризуемыми тензором а. Структура этой связи зависит от вида промывочной среды, от нагрузки, ее направления и др.

В случае вязкой ньютоновской жидкости уравнения связи ме­жду тензором напряжений и тензором скоростей деформации записываются в виде линейных зависимостей Навье — Стокса

охх = 2ц дюх/дх — ц сИу у; сху = ц (дих/ду + дюу/дх);

2

Суу = 2й дьу1ду — у Ц сНу V; схг = ц (дъх! дг + диг! дх ^} 24)

огг = 2ц дюг/дг — у ц (Ну у; ауг = ц (дюу/дг + дюг/ду),

где (х — коэффициент вязкости.

Для того чтобы перейти к температуре, необходимо восполь­зоваться термодинамическими соотношениями между внутренней энергией и удельным объемом 1/р, давлением и температурой:

(1и = [-р + Т (др/д’Г) р] й (1/р) + с1Т, (1.25)

где Су — удельная изохорная теплоемкость.

Уравнения (1.17), (1.18а), (1.20) совместно с равенствами (1.21) или (1.22), (1.23), (1.24), (1.25) составляют уже замкнутую систему для определения основных параметров промывочной среды (1.14). Однако, как уже отмечалось, скважина не является изолированной в тепловом отношении системой. Она постоянно взаимодействует с окружающим массивом. При исследовании те­чения в скважине необходимо учитывать процессы переноса теп­лоты в окружающем ее массиве горных пород. С этой целью на­пишем уравнение энергии для пород, считая их неподвижной не — деформируемой средой. Оно выводится из общего уравнения (1.20а), если в последнем положить

р (Их сэф (/п) <#п, V 0,

6 = 0, ч = — А„у/п.

Тогда

с, ф(/„) ^ = «V 0-М = -£■ (1.-Й-) +Т5Г (к %-) +

+!(1„1г). <> 2б>

где — температура пород; Я, п — коэффициент теплопроводности пород; сЭф(/п) — объемная эффективная теплоемкость пород.

При бурении скважин в мерзлых породах или при бурении с одновременным замораживанием процесс переноса теплоты в окружающем скважину массиве сопровождается фазовым перехо­дом содержащейся в нем влаги. В этом случае теплоемкость сЭф зависит не только от температуры, но и от теплоты фазового пе­рехода. Так, если фазовый переход происходит при фиксированной температуре 1 = (атр, то согласно работе [56] можно записать

Ссф (*п) = Сп (О + (<П — *агр), (1 -27)

где

( С При /п <С ^агр»

Сп I с+ При tп > tarp;

с~ и с+—теплоемкость мерзлой и талой породы соответственно; •фу — объемная теплота фазового перехода, б — дельта-функция

Дирака.

Для решения задачи (1.14), строго говоря, следует решить си­стему уравнений (1.17), (1.18), (1.20) и (1.26) с соответствующими граничными условиями и соотношениями, устанавливающими

связь между параметрами. Решение такой сложной нелинейной системы уравнений даже при современном высоком уровне вычис­лительной техники практически невозможно. С другой стороны, не все процессы, происходящие в циркуляционной системе сква­жины, одинаково влияют на формирование и изменение полей дав­ления, температуры и скоростей в рассматриваемой области. Кроме того, основные параметры, характеризующие эти процессы, как правило, определяются приближенно. Это позволяет отказаться от необходимости решения полной системы уравнений и перейти к рассмотрению более простых соотношений, получаемых из соот­ветствующего анализа общей математической модели [17, 31, 41, 46, 68].

Комментарии запрещены.