Бурение грунтовых зондов, установка энергетических колодцев

В рассмотренных выше теоретических построениях наиболь­шее сомнение может вызывать достоверность приближенного учета количества теплоты, рассеивающейся в единицу времени в окру­жающем пенетратор горном массиве, тем более что даже в усло­виях установившегося режима бурения плавлением суммарный тепловой поток на подогрев породы от ее естественной темпера­туры до температуры плавления впереди движущегося забоя ф3 и на рассеивание в окружающем массиве в радиальном направле­нии (34 составляет наибольшую долю в общем тепловом балансе, который выражается равенством (5.61). Анализ теплофизических свойств основных типов горных пород показывает, что в общем балансе тепловой мощности на бурение плавлением более 70 % приходится на их суммарный прогрев в массиве до температуры плавления, менее 20 % — на собственно плавление и менее 10 % — на перегрев образующегося расплава.

Таким образом, максимальная возможная погрешность в теп­лотехнических расчетах процесса связана прежде всего с опреде­лением суммарного теплового потока не только на полезный про­грев расплавляемого объема горной породы, но и на бесполезное радиальное рассеивание в окружающий массив через боковую поверхность призабойной зоны скважины за счет теплопровод­ности пород. Его точное определение представляет значительную трудность, так как при детальном исследовании требует решения двухмерной нестационарной задачи теплопроводности, которая при наличии фазового перехода на свободной границе становится еще и существенно нелинейной. Упрощенная постановка этой задачи мо­жет приводить к большим погрешностям при расчетах.

Представим суммарный тепловой поток на рассеивание в мас­сиве (для простоты без учета оплавления стенок скважины) в виде

С/ = ккпИ2сгрт (/ягр — 1Т) V, (5.77)

где ^—безразмерный коэффициент, учитывающий дополнитель­ный прогрев окружающего пенетратор массива (за пределами фронта плавления горной породы).

Предполагается, что коэффициент /г* учитывает все особен­ности протекающего в зоне забоя тепломассообменного процесса и зависит как от технологических параметров (активной тепловой мощности пенетратора, осевой нагрузки), так и от технических (форма и размеры пенетратора, теплофнзические свойства горной породы и ее расплава).

Воспользуемся полученным в работе [65] точным решением интегрального уравнения для плотности теплового потока, посту­пающего с поверхности плавления забоя в горную породу, кото­рая для нагревателя с параболической формой греющей поверх­ности (или если ее можно аппроксимировать параболической) мо­жет быть вычислена по формуле

Ре е~а ^

<7 = —^————- 7 = — ■, (5.78)

а2 Е1 (-а2) VI + Ь/ (г)]2

где а2 = Ре/(8/7)—безразмерный параметр; Ре = 2иУ?/ат — без­размерная скорость бурения (число Пекле); Н — Н/Я— безраз­мерная высота пенетратора; у'(г) — уравнение параболоида

вращения (или близкого ему по форме тела вращения) в цилин­

дрической системе координат; Я — радиус скважины (или пенетра­тора в верхнем его сечении), м; Я — высота пенетратора, м.

Для удобства вычислений сложная функция от а2е°гЕ1(—а2) в выражении (5.78) аппроксимирована в работе [15] логарифми­ческой зависимостью

а2е«2ЕЦ-а2) = -^1п[(1 +^)2(1 + |г)] (5.79)

В соответствии с выражением (5.79) равенство (5.78) примет

вид

<7 =—————- ————————- Г — -‘г-…. гг (5.80)

а2 1п [(1 + 1/а2)2 (1+2/а2)] V» + [у’ (О!2

или с переходом к размерным величинам

(5.81)

4СтРт (^агр ^т) ^

а2 1п [(1 + 1/а2)2 (1 + 2/а2)] ^+у'(г)2′

где

2___ Р2стр гу

Значение высоты Н можно задавать в расчетах или опреде­лять, зная выражение для профиля параболоида вращения вокруг оси скважины, при г — Я. Если рабочая поверхность пенетратора является близкой к параболоиду вращения, то таким же методом определяется его высота. Так, для поверхности вращения, обра­зованной цепной линией, высота Н реального пенетратора опреде­ляется выражением (5.65) при условии г — /?.

/

(5.82)

С 0,5 1 1,5

Суммарный тепловой поток через по­верхность расплавляемого забоя в массив горных пород определится выражением [65]

где « —длина дуги образующей рабочей по­верхности пенетратора (при г = Я).

(5.81) и заменяя

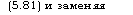Подставляя в это выражение равенство с/в = У1 + [у’ (г)]2 йг, получаем

(5.83)

4зт/?2СтРг (<агр ^т) ^ а2 1п [(1 + 1/а2)2 (1 + 2/а2)]

Приравнивая соотношения (5.77) и (5.83), находим выражение для искомого коэффициента

!п 1(1 + 4В)2(1 +8В)] ’ ^5-84^

где В — атН/(Я2и) — безразмерный параметр.

Чтобы проследить характер функции /г*, = /(Б), проведем рас­четы для случая бурения плавлением с помощью пенетратора диа­метром 50 мм по базальту [16] при следующих исходных дан­ных: = 0,025 м; £агр = 1200°С; £Т = 20°С; рт = 2,6-103 кг/м3;

ст= 1.05-103 Дж/(кг-°С); Ат= 1,8 Вт/(м-°С).

Результаты расчета представлены графически на рис. 5.7, по­казывающем почти прямую пропорциональную зависимость теп­лового потока на рассеивание в массиве от высоты пенетратора

Н, выражаемой параметром В при прочих неизменных условиях.

Имея теперь аналитическое выражение для коэффициента можем оценить достоверность полученного здесь приближенного решения задачи о скорости бурения горных пород плавлением в смысле полноты учета суммарного теплового потока на рассеива­ние в массиве. Для этого представим суммарный тепловой поток Ф — С?3 + С?4 с помощью полученных выше приближенных выра­жений (5.55) и (5.60) также без учета оплавления стенок сква­жины (6 = 0) в виде

О" = ЫЯ2стрти + 4Я У яАтстртЯ) (/агр — /т). (5.85)

Несмотря на то что формула (5.77) в сочетании с выраже­нием (5.84) для кх, полученным аппроксимацией точного реше­ния, не может рассматриваться в качестве эталона, есть смысл сравнить с ней расчетным путем заведомо приближенную фор­мулу (5.85).

Расчеты количества теплоты, рассеивающейся в единицу вре­мени в окружающем массиве, произведены для случая бурения

Расчетные значения количества теплоты, рассеивающейся в единицу времени в окружающем пенетратор массиве, Вт

Высота пене-	Формула	Скорость бурения плавлением, м/ч
тора, Я, м	0,36	0,72	1,С8	1,44	1,80	2,16	2,52	2,86	3,24	3,60
0,025	(5.77) (5.85) (Q"—Q’)IQ’, %	1037 900 — 13,2	1708 1643 -3,8	2353 2359 +0,3	2985 3062 +2,6	3637 3757 +3,3	4251 4445 +4,6	4915 5130 +4,4	5516 5810 +5,3	6171 6486 +5,1	6806 7161 +5,2
0,050	(5.77) (5.85) (Q"-Q’)/Q’. %	1360 1024 —24,7	2075 1818 — 12,7	2751 2574 -6,4	3116 3311 -3,1	4048 4034 -0,3	4706 4748 +0,9	5357 5457 + 1,9	5971 6160 +3,2	6604 6858 +3,8	7274 7554 +3,8
0,75	(5.77) (5.85) (Q"-Q’)IQ %	1651 1122 -32,0	2404 1957 -18,6	3112 2744 — 11,6	3795 3507 —7,6	4459 4254 -4,6	5123 4990 -2,6	5756 5717 -0,7	6426 6437 +0,2	7059 7153 + 1,3	7717 7864 + 1,9
0,100	(5.77) (5.85) (Q"—Q’)/Q’, %	1923 1206 -37,3	2720 2075 -23,7	3454 2889 — 16,4	4213 3675 -12,8	4838 4442 -8,2	5503 5196 -5,6	6154 5939 -3,5	6831 6676 —2,3	7457 7405 -0,7	8096 8130 +0,4

плавлением по базальту при тех же приведенных выше исходных данных применительно к пенетратору диаметром 50 мм и реальной высотой 25, 50, 75 и 100 мм при разных значениях скорости буре­ния плавлением как функции активной мощности пенетратора Na. Необходимые при расчетах по формуле (5.85) значения высоты эквивалентного цилиндра для различных значений реальной высоты пенетратора определялись с помощью соотношения

I________________ I______________ 1_______________ !————————— L. 2 4 G 8 10 0,72 1,44 2,16 2,88 3,6

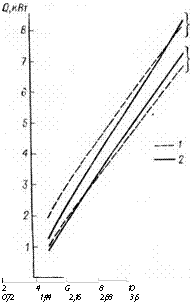Яц = V/ (nR2) и выражений (5.65) и (5.68). Результаты расчетов сведены в табл. 5.3 и частично представлены графн — I чески на рис. 5.8.

Анализ данных — табл. 5.3 и рис. 5.8 показывает прежде всего весьма близкое совпаде­ние расчетов по обеим форму­лам (5.77) и (5.85). В боль­шинстве случаев расхожде­ние не превышает ±5%, а при реальной высоте пенетра­тора Н, равной диаметру и

Рис. 5.8. Расчетные зависимости ко­личества теплоты, рассеивающейся в единицу времени в окружающем пе­нетратор массиве от скорости буре — ‘ кия плавлением при Я = 0,025 м (/)

%’°1чм/с и Я = 0,1 м (//).

/ — по формуле (5.77); 2 —по формуле (5.85).

превышающей его, и скоростях бурения плавлением выше 2 м/ч можно говорить о полном совпадении. Тот факт, что при малых скоростях бурения плавлением (как функции активной мощности) превышение расчетных значений рассеивающейся в массиве теп­лоты по формуле (5.77) в сравнении с формулой (5.85) возрастает с увеличением высоты пенетратора И, говорит в пользу послед­ней, как и сам характер графиков на рис. 5.8. Это можно объяс­нить более грубой приближенностью логарифмической аппрокси­мации точной зависимости [65] в области малых значений V и больших значений Н, чем полученное здесь приближенное ре­шение.

Формулу (5.85), приближенно выражающую суммарный поток теплоты, рассеивающейся в массиве, можно считать практически достоверной или во всяком случае вполне пригодной для оценки этой доли тепловой мощности в общем ее балансе (с учетом плав­ления горной породы и перегрева расплава).

Комментарии запрещены.