Бурение грунтовых зондов, установка энергетических колодцев

Режим замораживания неустойчивых слабосвязных или не­связных влажных и обводненных горных пород осуществляется не­посредственно в процессе бурения скважины и определяется теп­ловым взаимодействием потока низкотемпературной промывочной среды — хладоносителя со стенками скважины, керна и поверх­ностью подвижного забоя. В результате понижения естественной температуры породы при теплообмене до отрицательных темпера­тур и связанного с этим замерзания содержащейся в ней влаги, на стенках скважины и керна, а также на поверхности забоя про­исходит формирование прочного и водонепроницаемого ледопород — ного слоя.

Смысл решения задачи о промерзании пород в процессе буре­ния скважины сводится к отысканию условий, при которых на за­бое можно создавать и поддерживать в течение всего процесса углубки скважины ледопородный слой заданной толщины. Считая, что прочностные свойства ледопородного слоя на стенках сква­жины и керна определяются однозначно глубиной опережающего промерзания породы забоя, остановимся подробнее на отыскании условий, при которых заданная глубина промораживания забоя может быть обеспечена. Поскольку в данном случае нас интере­суют тепломассообменные процессы, происходящие вблизи забоя скважины, то в дополнение к ранее сделанным упрощениям на­шей основной задачи, введем следующие допущения:

— начальная температура пород постоянна — tn0 = const;

— в призабойной зоне устанавливается квазистационарный ре­жим теплообмена, т. е. dt, 2/<Зт—>-0;

— температура промывочной среды — хладоносителя в зоне за­боя скважины поддерживается отрицательной и может быть оп­ределена выражением

t3 = h+h-<t^, (3.1)

— бурение скважины осуществляется со скоростью 1>(т) = = const, обеспечивающей заданную глубину промерзания пород 6 = //агР — Я3;

— тепловой поток в зоне забоя одномерен и направлен вдоль оси скважины, так как толщина промерзания пород забоя в про­цессе бурения много меньше радиуса скважины, т. е. 6 <С Rq.

С учетом принятых допущений в качестве математической мо­дели для определения условий промерзания породы забоя сква­жины в процессе бурения будем рассматривать одномерную задачу

Рис. 3.1. Схема для построе­ния математической модели процесса бурения с одновремен­ным замораживанием породы забоя скважины.

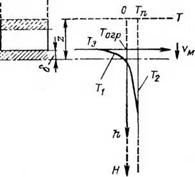о распространении теплоты в двухфазной среде для полупростран­ства, ограниченного поверхностью забоя скважины z = Н3, пере­мещающейся в направлении движения фронта промерзания с по­стоянной скоростью u(T) = const (рис. 3.1).

Уравнение переноса теплоты теплопроводностью (1.26) для об­ласти III (рис. 1.12) с учетом принятых упрощений может быть представлено двумя аналогичными уравнениями соответственно для мерзлой и талой зон забоя при начальных и граничных усло­виях

dt~ д2<~

(3.2)

-аГ = ап-а?-. и* <z<tfarp; dt+ . Л+

дт n dz2 ‘ arP

а) T T0, tn /по,

dt~ , N

б) т > T0, z = H3> к = a3 (Л. — tj;

, _ dt~ . dt„ rf# n

в) T > T0, Z= H arp, /п hn An ^ ;

г)т>т0, z->oo, /п — Jn0->0.

Здесь an — коэффициент температуропроводности породы, м2/с; а3 — коэффициент теплоотдачи от промывочной среды — хладоносителя к поверхности забоя, Вт/(м2-К); индексами «—» и «+» обозначаются величины, характеризующие свойства породы забоя в нормальном и мерзлом состояниях;

г^ = ^Рск. п^п = ^(1-^п)Р0^п

-—объемная теплота фазового превращения, Дж/м3; г|)-—удель­ная теплота агрегатного перехода, Дж/кг; рск. п — объемная плот­ность скелета породы, кг/м3; — влажность породы, доли еди­ницы; Кп — безразмерный коэффициент пористости; ро — мине­ральная плотность породы, кг/м3.

Для обеспечения в процессе бурения скважины опережающего промерзания породы забоя на толщину б необходимо и доста­точно, чтобы скорость промерзания породы по крайней мере рав­нялась скорости бурения V.

Следовательно, задачу (3.2) необходимо дополнить условием

<1Н3

^агр (3.3)

V =

ёт

й т

С помощью условия (3.3) можно определить скорость бурения, при которой будет обеспечена заданная глубина промерзания по­роды на забое.

Для анализа и решения задачи (3.2) с условием (3.3) перей­дем к следующим безразмерным переменным и критериям по­добия:

^нО вп ———— г—: *3 »ПО

0 Ро

и 6

Ре = —

агр <3 — (по ‘ _ ип С1 ~ То) .

агр ‘

г =

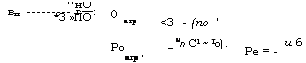ВЦ = — Ко =

к — К ■ Кк~К’

сп Рп I ^з ^пО I

6 и значительного превышения времени бурения с заморажива­нием т — то над временем распространения температурных возму­щений в слое 6 безразмерное время, характеризующее процесс промерзания породы впереди подвижного забоя, будет намного

1 двп Р°аТр дг 1 дв+ Р°а+гр дг а) т= 1, 0П = ( ); б) т > 0, N II О 5©+ дг в) т > 0, 2 = 1, ©п = г) т > 0, г~*оо, 0+ Анализ задачи (3.4)

Ре Ре

<?©п агр д/:2

агр

о<г< 1; двГ1

(3.4)

1 < оо;

дг

дг

дв:,

д@п дг

— Ко Ре;

Кь-

агр»

-‘агр)

дг

0.

Тогда задача (3.2) может быть представлена в форме следую­щих выражений с безразмерными величинами:

больше единицы:

(х — тп)

ИОагр-—V — •~>ї-

«»п д2&; •агр dZ dZ2 ’ _ + а2е+ -агр dZ dZ2 ’

Следовательно, первым слагаемым левой части системы урав­нений (3.4) можно пренебречь. В результате упрощения получим

0<г<1;

(3.5)

1<г < сю;

а) Z = О, -^- = В!3(вп — 1);

б) 2=1, 0п = ©п+ = ©агр, д-ж~ КоРеагР;

в) Z —> оо, 0„ —► 0.

Решение задачи (3.5) будем искать в следующем виде: f 0п =СГ ехр(— Реагр, Z) + С;Г;

I 0П+ = СГ exp (- Pea+rp, Z) + С2+,

где СГ и С* — неизвестные постоянные, которые определяются условиями «а» — «в» задачи (3.5).

В окончательном виде решение задачи (3.5) может быть пред­ставлено выражениями

0- = 0 Pearp + Bi3 t1 — ехР (- Реагр тЩ,

аГР Pearp+Bi3[l-exp(-PearpT2)] exp (— Pe~z) — exp (— Ре-)

+ В i3 —— ^ У 2LЈf., 0<Z<1; (3.7)

Pea”rp+Bi3ll-exp(-Pea-rp)J ’

0it = 0arp exp [—-Реагр (z1)], KZ<oo. (3.8)

Подставляя выражения (3.7) и (3.8) в условие «б» задачи

(3.5) и преобразуя полученное равенство с учетом условия (3.3), находим следующую зависимость для определения безразмерной скорости бурения с одновременным промораживанием породы за­боя Реагр:

_.шз (_: ехр..(- Ре^р) Ко + ^ е (3.9)

Perrp + Bi3ll-exP(-Pearp)j Кх агр

Здесь Ка = а+/ап.

При известной забойной температуре t3 уравнение (3.9) отно­сительно безразмерной скорости бурения Реагр является трансцен­дентным.

Комментарии запрещены.