 ПРОЕКТИРОВАНИЕ ТРАЕКТОРИЙ СКВАЖИН ДЛЯ НАПРАВЛЕННОГО БУРЕНИЯ
ПРОЕКТИРОВАНИЕ ТРАЕКТОРИЙ СКВАЖИН ДЛЯ НАПРАВЛЕННОГО БУРЕНИЯ
Методика направленного бурения скважин включает и себя решения следующих задач: 1) обоснования и выбора рациональной для данных условий бурения траектории скважин; 2) расчета траектории скважины; 3) выбора технических средств и режимов направленного бурения.
Траектория скважины выбирается с учетом се назначения, геологических условий бурения, закономерностей естественного искривления, технических возможностей п"экономических соображений.
Наиболее существенным требованием при бурении геологоразведочных скважин является сохранение проектной плотности разведочной сети при подееченин залежи полезного ископаемого. Это означает, что отклонение ствола скважины от заданной точки нодеечепия не должно превышать определенной величины,
т. е. скважина должна быть направленной. При этом се проектная траектория может быть задана произвольно, без предварительного расчета, или выбрана на основе анализа закономерностей естественного искривления скважин н результатов предварительного расчета.
Первый способ задания траекторий приемлем лишь в наиболее простых геологических условиях и при ограниченной глубине скважин. Чаще всего в этих условиях проектируются прямолинейные вертикальные или наклонные скважины. Проведение скважин значительной глубины по вертикальной прямолинейной траектории требует применения предупредительных мер или искусственного искривления, что ведет к снижению производительности и удорожанию буровых работ. Оно может быть оправдано лишь при бурении скважин в специальных целях или в особо благоприятных геологических условиях (изотропные породы горизонтального залегания). Наиболее рациональным является метод направленного бурения скважин по типовым траекториям, предварительно рассчитанным по средним значениям интенсивности естественного искривления ранее пробуренных скважин на равных интервалах их глубин при установившейся для данного месторождения технологии бурения.
С этой целыо, прежде всего, производят обработку данных ипклинометрическіг* измерений и строят вертикальные и горизонтальные проекции трасс ранее пробуренных скважин.
Данные пиклипометрнческих измерений записывают в табл. 11.1.
|
Таблица 11.1
|
Приращение горизонтального смещения забоя рассчитывают ио формуле
Ал:» ^ (La — £„_,) sin — Ql-L. . (і 1.4)
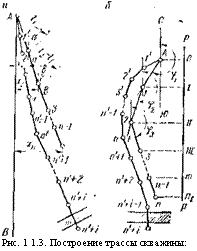
Для построения горизонтальной проекции трассы скважины через точку Л, изображающую устье скважины, проводят прямую с азимутом аі и откладывают па пей отрезок А — 1, равный Ал’, (рис. 11.3,а). Через точку / проводят прямую с азимутом а-,, па которой откладывают отрезок 1—2, ранный Лл’2. Построение продолжают подобным же образом для всех остальных то-
чек. Соединив точки А, 1. 2, … прямыми, получают положение трассы сквпжнны к плане. Вертикальную проекцию скнлжнны можно построить п любой вертикальной плоскости, например, нкрест простирания пластов, как показано па рис. 11.3,6. Для этого через точки А, 1, 2, … опускают перпендикуляры па лн — пию РР, изображающую плоскость профиля скважины, и получают точки 0, т. Отрезки 0—/, 0—11, 0—т представ
ляют собой смещения забоя хи Хг, . ■ х по профилю РР. Их измеряют и записывают в табл. 11.1.
|
Рнс. 1 1.3. Построение трассы скважины: |
 Затем из точки А (рис. 11.3, а) описывают дугу радиусом в соответствующем масштабе.
Затем из точки А (рис. 11.3, а) описывают дугу радиусом в соответствующем масштабе.
На расстоянии х параллельно вертикали АВ проводят прямую аа, получая на пересечении ее дугой точку 1. Из точки 1 описывают дугу радиусом и
на расстоянии х% проводят прямую ЬЬ параллельно вертикали АВ. Их пересечение дает точку
2. Подобным же образом строят все остальные точки. Соединяя точки А, 1, 2, … прямыми, получают вертикальную проекцию трассы скважины па плоскость профиля РР.
|
и вертикальная проекции (профиль); 6 — горизонтальная проекция (план) |
 Для изучения закономерностей естественного искривления скважин их разбивают на группы с учетом геологических и технико-технологических особенностей их бурения, чтобы образовать качественно однородные в статическом смысле совокупности (выборки). Для каждой группы определяют значения средних арифметических величин зенитных и азимутальных углов или нх приращений у и средние квадратические отклонения о через равные интервалы длины стволов:
Для изучения закономерностей естественного искривления скважин их разбивают на группы с учетом геологических и технико-технологических особенностей их бурения, чтобы образовать качественно однородные в статическом смысле совокупности (выборки). Для каждой группы определяют значения средних арифметических величин зенитных и азимутальных углов или нх приращений у и средние квадратические отклонения о через равные интервалы длины стволов:
|
(И.5) |
![]() У + У* "Ь • ■ • ~~Уп
У + У* "Ь • ■ • ~~Уп
|
£ [ус—уУ |
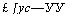
|
(11.6) |
![]()
|
где 1/{(£=1, 2, …, п)—величины зенитных или азимутальных углов (или их приращений) на равных интервалах глубин скважин (например, 0; 25; 50; 100 и т. д.); « — число скважин дан поп группы в каждом интервале глубин. |
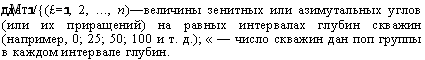 |
У ~~
Исследованиями Л. М. Курмашева, Ю. Т, Морозова н других па многих месторождениях разных районов страны было уста новлеио соотпетствне опытных данных и н юн ш о м стр н чсс к их измерений’закону нормального распределения, определяющему зависимость между возможными значениями случайной величины и соответствующими им вероятностями. При нормальном законе распределения среднее арифметическое характеризует наиболее вероятное значение случайной величины, около которого группируются все возможные значения совокупности. Разброс значений случайной величины около ее среднего арифметического характеризуется величиной среднего квадратического отклонения. Статистические закономерности распределения опытных данных инклинометрических измерений при условии соблюдения качественной однородности выборок (групп скважин) отражают закономерный характер естественного искривления скважин, что и позволяет использовать средние значения измеренных ранее величин для прогнозирования с определенной. степенью точности траекторий вновь буримых скважин в тех же геолого-техниче — ских условиях. Отклонение фактической траектории скважины от проектной при этом, конечно, не исключается, но оно будет иметь характер случайного явления, вероятность которого можно оценить заранее.
Практически расчет проектной траектории скважины сводится к реализации ее математической модели, полученной в результате статистической обработки данных инклинометрических измерений ранее пробуренных скважин. Математические модели чаще всего представляются в виде уравнения зависимости величины зенитного угла 0 (или интенсивности зенитного искривления) от длины ствола скважины:
0 = /(1) или *е = /(1). (11.7)
При больших азимутальных искривлениях могут применяться модели, описывающие изменение полного угла искривления р = = по практически всегда стремятся осуществить бурение по плоскоискривленной траектории, задавая скважины вкрест простирания пород и сводя, таким образом, азимутальное искривление к минимуму. Математическая модель может быть получена в виде уравнения прямой линии, окружности или плоской крипон, например
10 — а 4-Ы, (11.8)
где и и Ь — опытные коэффициенты, определяемые методом наименьших квадратов по данным инклинометрических измерений.
Учитывая, что получим уравнение профиля еква-
й1-
жины в виде
Граничное условие напишем в виде
I — О О 0„. (11.10)
Тогда окончательно
0-00 + 01+-^1. ^ (П И)
Эта зависимость, как показано Ю. Т. Морозовым, хорошо аппроксимирует зенитное искривление скважин при алмазном бурении в анизотропных и перемещающихся породах.