Бурение грунтовых зондов, установка энергетических колодцев

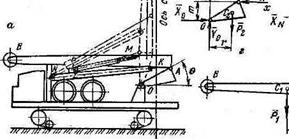
На рис. 4.6, а показана самоходная буровая установка в транспорт­ном положении. Для бурения скважины мачта должна быть поднята в рабочее положение. Мачту поднимают с помощью гидроцилиндра LN, при этом, помимо цилиндра, в движение приводятся сразу четыре элемента: гидроцилиндр, верхняя секция мачты А В с силой тяжести 7′,, нижняя секция мачты О А с силой тяжести Р2 и опорный

стержень NK с силой тяжести Р3. Ставится задача: для момента

страгивания мачты определить усилия, возникающие в шарнирах N, , L, К, А и О, а также усилие гидроцилиндра F. Введем следующие

допущения: 1) сила тяжести гидроцилиндра по сравнению с другими

91

Рис. 4.6. К расчету усилий в шарнирах при подъеме буровой мачты из транспортного положения в рабочее

о м

*

а

элементами мала и ею можно пренебречь; 2) трение в шарнирах

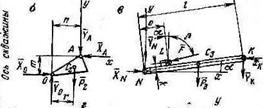
незначительно и им также можно пренебречь; 3) задача является плоской, т. е. все элементы крепления относительно вертикальной, продольной станку, плоскости расположены симметрично, и, следова­тельно, усилие в (гаждом шарнире, например, в опоре А (а их две) можно определить делением реакции опоры пополам (все размеры в буквенных обозначениях показаны на рис. 4.6,6, в, г); 4) сила тяжести Р3 стержня NK приложена в его середине; 5) скорость страгивания мачты весьма мала.

Задачу будем решать, рассматривая данную конструкцию как систему тел. Направление осей координат для всех тел принято одинаковым. На каждое тело действует плоская произвольная система сил и, таким образом, для каждого тела можно составить три уравнения равновесия.

Рассматривая равновесие нижней секции мачты, получаем следу­ющие три уравнения (см. рис. 4.6, б):

(4.66) (4.67) (4.68)

£^=0, Хо-Хл=0;

1^=0, Yq — P2 — Уд = 0;

£m0(fi) = 0, — P2r-YAn+XAm=0.

Рассматривая равновесие стержня, получим еще три уравнения (см. рис. 4.6, в):

Г

0;

(4.69)

0;

(4.70)

X mN {^) = 0, —P3(//2)cosa+A’JC/sina- — YK /cos a+Fsin (P+a)k—Fcos (P+a)e=0.

Наконец, рассматривая равновесие верхней секции мачты, получим последние три уравнения статики:

Fsin $ + Хк + ХА = 0, (4.72)

Pi + Fcos Р+Ул+Ук = 0, (4.73)

Pi d— YKa—Fb cos P—Fc sin p = 0. (4.74)

Таким образом, мы получили девять уравнений равновесия, содержащих девять неизвестных величин F, Х0, XN, YN, У0, Хк, YK, ХА и YА. Следует учитывать, что реакции шарниров для попарно соединенных тел равны по модулю и противоположны по знаку. Решая эти девять уравнений совместно, находим искомые величины. Равновесие цилиндра LM не рассматривается. Поскольку, принято, что сила тяжести цилиндра равна нулю, последний может быть отождествлен с невесомым стержнем, а реакция — невесомого стержня направлена вдоль стержня, следовательно, усилие в шарнире L равно F. ,

Из-за громоздкости полученных формул ниже приведено полное алгебраическое выражение только для силы F:

_ 2Pi l(an sin a+md cos a— nd sin a)+2P2 lar x

t

2{rial sin a cos a—nbl sin a—mal sin a sin p+

(4.75)

x sin a+F3 Ima cos a +_ ml(b cos p+с sin p) cos a+та [ATsin (a+p)—e cos (a+P)]}

Для исходных данных Pi = 3500 H, P2=1500 H, Р3 = 1000 Н, <7=3,5 м, а=1м, с = 0,5 м, Ь=2 м, р=75°, а=10°, г=0,8 м, и—1,2 м, те=0,7 м, /= 5 м, е= 1 м, /с=0,5 м неизвестные реакции опор и сила F будут иметь следующие примерные значения: F—19 200 Н,

Хк= -29980 Н, YK= —7140 Н, Л^=11430Н, УЛ = 5670Н, Уо=П430 Н, У0 = 7170 Н, *^=-11430 Н и yw=-1150H. Знаки минусы при числовых значениях реакций опор показывают, что соответствующие силы направлены в сторону, противоположную показанной на рисунке.

Полная реакция опоры, например, А определится по формуле

Ra={Xa+Y2a)112. (4.76)

Выше мы определили реакции всех шарнирных опор только для одного положения мачты—начального. Однако в процессе подъема мачты реакции опор будут изменяться, причем необязательно в мень­шую сторону. Поэтому при реальных инженерных расчетах необ­ходимо определять усилия в шарнирах для любых положений мачты.

Это позволит для каждого шарнира установить максимальное усилие и последующий расчет самого шарнира вести с учетом этого усилия.

Порядок определения максимальных усилий может быть принят следующий. Поскольку рассматриваемый механизм подъема мачты имеет одну степень свободы, в качестве аргумента может быть выбран один обобщенный параметр, например угол 0 (см. рис. 4.6, а), определяющий положение нижней секции мачты О А. Все реакции опор определяются в функции этого угла. Далее, берется частная производная по углу от реакции опоры и приравнивается к нулю. Определяется угол 0, при котором соответствующая реакция приоб­ретает максимальное значение и затем находится это значение. Операция производится для каждой опоры. Даже для такой срав­нительно простой задачи, как рассматриваемая, соответствующие уравнения будут весьма громоздки и могут быть решены только с помощью ЭВМ.

Полезно также отметить, что с помощью ЭВМ можно осуществить оптимизацию данного подъемного механизма. Например, может быть решена задача о рациональном взаимном расположении опор А, К, L, М, N и О (при определенных наложенных ограничениях), обеспечивающем минимальное значение подъемного усилия F, и т’. д.

Приведенная выше задача рассмотрена на основе чисто статических представлений. Однако, строго говоря, задача является динамической. В момент страгивания мачты с места в опорах неизбежно возникнут динамические составляющие реакции связей (как и. при остановке). Помимо того, в процессе подъема мачты в отдельных элементах механизма подъема могут возникать ускорения. Все это поддается строгому расчету, но задача становится столь громоздкой, а уточнение результата по сравнению со статическим расчетом столь незначитель­ным, что от строгого решения заранее отказываются, компенсируя соответствующие’ неточности введением некоторых коэффициентов запаса.

Комментарии запрещены.