Interpretation of Shut-in Pressures
Interpretation of Shut-in Pressures
When an influx has occurred and has subsequently been shut-in, the pressures on the drillpipe and the annulus at surface can be used to determine:
In order to determine the formation pressure, the kill mudweight and the type of influx the distribution of pressures in the system must be clearly understood. When the well is shut-in the pressure at the top of the drillstring (the drillpipe pressure) and in the annulus (the annulus pressure) will rise until:
(i) The drillpipe pressure plus the hydrostatic pressure due to the fluids in the drillpipe is equal to the pressure in the formation and,
(ii) The annulus pressure plus the hydrostatic pressure due to the fluids in the annulus is equal to the pressure in the formation.
It should be clearly understood however that the drillpipe and annulus pressure will be different since, when the influx occurs and the well is shut-in, the drillpipe will contain drilling fluid but the annulus will now contain both drilling fluid and the fluid (oil, gas or water) which has flowed into the well. Hence the hydrostatic pressure of the fluids in the drillstring and the annulus will be different. A critical assumption that is made in these calculations is that the influx travels up the annulus between the drillstring and the borehole rather than up the inside of the drillstring. This is considered to be a reasonable assumption since the influx would be expected to follow the flow of fluids through the system when they enter the wellbore.
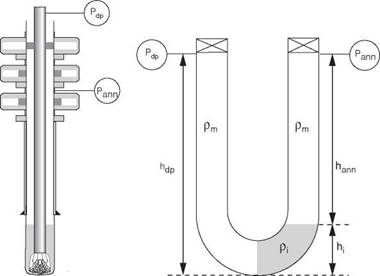
It is convenient to analyse the shut-in pressures by comparing the situation with that in a u-tube (Figure 9). one arm of the u-tube represents the inner bore of the drillstring, while the other represents the annulus. A change of pressure in one arm will affect the pressure in the other arm so as to restore equilibrium.
|
Figure 9 Interpretation of wellbore pressures as a u-Tube |
%
|
DRILL PIPE |
|
1000 2000 3000 4000 5000 |
|
8000 9000 |
|
Pressure in 1000 PSI |
|
6000 |
|
ANNULUS
Pressure in 1000 PSI |
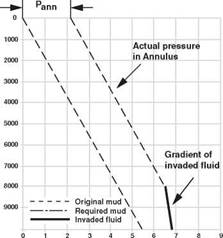
Figure 10 Pressure profile in drillpipe and annulus when well shut-in
The pressure at the bottom of the drillstring is due to the hydrostatic head of mud, while in the annulus the pressure is due to a combination of mud and the formation fluid influx (Figure 10). Hence, when the system is in equilibrium, the bottom hole pressure will be equal to the drill pipe shut-in pressure plus the hydrostatic pressure exerted by the drilling mud in the drillstring. Hence:
Pdp + Pmd = Pbh Equation 1
where,
Pdp = shut in drillpipe pressure (psi) pm = mud pressure gradient (psi/ft) d = vertical height of mud column (ft)
Pbh = bottomhole pressure (psi)
If the well is in equilibrium and there is no increase in the surface pressures the bottomhole pressure must be equal to the formation pore pressure :
P = P Pbh = Pf
Equation 2
Since the mudweight in the drill pipe will be known throughout the well killing operation and Pdp can be used as a direct indication of bottom hole pressure (i. e. the drillpipe pressure gauge acts as a bottom hole pressure gauge). No further influx of formation fluids must be allowed during the well killing operation. In order to accomplish this the bottom hole pressure, Pbh (= Pdp + pmd) must be kept equal to,
or slightly above, the formation pressure, Pf. This is an important concept of well control and the one on which everything else is based. This is the reason that this technique for well killing is sometimes referred to as the constant bottom hole pressure killing methods.
On the annulus arm of the U-tube, the bottom hole pressure is equal to the surface annulus pressure and the combined hydrostatic pressure of the mud and influx:
Pann + hiPi + (d-hi) Pm = Pbh Equation 3 where,
Pann = shut-in annulus pressure (psi)
hi = height of influx (ft)
pi = pressure gradient of influx (psi/ft)
and to achieve equilibrium :
P = P Pbh = Pf
Equation 4
one further piece of information can be inferred from the events observed at surface when the well has been shut-in. The vertical height of the influx (hi) can be calculated from the displaced volume of mud measured at surface (i. e. the pit gain) and the cross-sectional area of the annulus.
hi = V A
Equation 5
where,
V = pit gain (bbls)
A = cross section area (bbls/ft)
Both V and A (if open hole) will not be known exactly, so hi can only be taken as an estimate.
Since an influx has occurred it is obvious that the hydrostatic pressure of the mud colom was not sufficient to overbalance the pore pressure in the formation which has been entered. The pressure in this formation can however be calculated from Equation 1:
Pf = Pbh = Pdp + Pmd Equation 6
%
|
X |
Since all of the parameters on the right hand side of this equation are known, the formation pressure can be calculated.