Бурение грунтовых зондов, установка энергетических колодцев

Из практики известен ряд определенных материалов, которые могут использоваться в качестве катализаторов для некоторых реакций. Учитывая чрезвычайную слож­ность обобщенного описания явления, авторы сочли воз­можным остановиться на квантово-механической интер­претации наиболее простого случая — реакции разряда водорода на различных металлах. Из экспериментов из­вестно, что наилучшими катализаторами для водорода являются переходные металлы. Плотность тока обмена Jo связана с энергией хемосорбции водорода. При этом металлы условно разделяются на три группы.

Для металлов первой группы (в частности, Hg и РЬ) скорость реакции определялась скоростью разряда иона водорода:

, медленно

,Н+ + е——— — НаЛ,

Для второй группы (Fe, Ni, W, Та, Мо и т. д.) наибо­лее медленным является механизм десорбции:

 

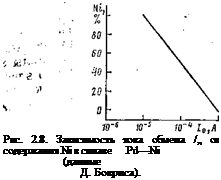Было высказано несколько гипотез о причине воздей — .ствпя катализатора на скорость реакции водорода (иони­зацию). Особенно харак­терны исследования по сплавам металлов. Так, при изучении золото-пла­тинового сплава было ус­тановлено, что ток обме­на водородной реакции уменьшается с изменени­ем содержания золота и достигает минимума при 60% Аи. При таком со­ставе оказываются запол­ненными все d-связи. Для сплава платина—палла­дий отмечалась зависи­мость между прочностью связи атом водорода — металл и составом сплава. Инте­ресные зависимости от геометрических факторов струк­туры металла были получены при изучении сплава ни­кель— палладий. Палладий и никель имеют близкую электронную структуру, но разные размеры атомов. Учи­тывая, что энергия активации выше при больших разме­рах решетки (палладий), можно было ожидать увели­чения тока обмена с уменьшением содержания никеля (меньшие размеры решетки). Экспериментально под­тверждена такая зависимость (рис. 2.8). Заметим, что эти исследования носят чисто качественный характер, поскольку дефекты, неизбежно существующие на поверх­ности реальных тел, искажают параметры решетки и

(И

влияют на каталитические процессы (см. § 3.5). Иссле­дования на монокристаллах металлов подтверждают за­висимость реакции выделения водорода от параметров решетки. За последние годы появились более глубокие теории для объяснения роли материала электрода в про­цессе катализа. Продемонстрируем возможности совре­менных методов на одном примере. Было высказано предположение, что различия в каталитической актив­ности металлов, сплавов и диэлектриков тесно связаны с различиями в их электронной структуре и обусловлены ими. Отвлекаясь вначале от изменений, вносимых в элек­тронную структуру металла его поверхностью, влиянием электролита, дефектами решетки и т. и., на примере простейшей реакции ионизации атома водорода

H-vH+ + e — (2.44)

была сделана попытка [2.7] выявить те параметры элек­тронной структуры, которые определяют «ряд каталити­ческой активности» металлов по отношению к данной реакции, а также по отношению к реакции гидрирования, поскольку в реакциях гидрирования часто именно ста­дия (2.44) является лимитирующей. Выявленные па­раметры в свою очередь могут стать основой более пол­ной электронной теории катализа на металлах.

Рассмотрим задачу об энергетическом спектре атома водорода, внедренного в металл. Пренебрегая кристал­лическим потенциалом и считая, что он целиком экрани­руется электронами проводимости металла, запишем эффективное уравнение Шредингера в виде

{-Ы +’ф(0} U (r)= EU(г). (2.45)

Здесь т — масса «голого» электрона; Ф(г) —экрани­рованный кулоновский потенциал протона. Предполага­ется, что рассматриваемая задача обладает сферической симметрией.

Как известно, в зависимости от параметров потен­циалов Ф(г) могут реализоваться два случая: либо энергетический спектр Е является непрерывным, либо существуют еще и дискретные уровни. В первом случае электрон коллективизируется, а металлы, способствую­щие ионизации атома водорода, называются нами ката­лизаторами данной реакции.

Электронная структура металла аппроксимируется системой изотропных s- и d-зон. Статическую относи — 5-93 65

тельную диэлектрическую проницаемость можно пред­ставить в виде

+8rss + f5rdd~bBrsd~bCrds> (2.46)

где Erij описывает вклад в єг за счет г—/ переходов.

В Приближении свободных электронов Srss имеет вид

Здесь k—qaB, q—волновое число, аБ—боровский pa — ! диус; xs{EF)=Ns(EF)a2Be2; Ns — плотность электронных состояний на поверхности Ферми в s-зоне; е — заряд электрона. Для простых металлов ег(&)=1 +erss(k). Экранированный кулоновский потенциал Ф(г) определя­ется формулой

СО

-с, 2е2 С sin kr’ j f /г> л

, *(r) = —ZF)k^Wdk — (2-48)

Поведение Ф(г) при малых г (порядка нескольких десятых долей нанометра) определяется поведением er(k) при больших /г:

«Л%.о. = (т)’’■<£,)( (2-49)

Расчеты на ЭВМ показали, что и для г^>аБ потен­циал Ф(г) хорошо (с точностью до нескольких процен­тов) аппроксимируется своим значением для малых г.

Главный вклад в &r<id дают переходы из незаполнен­ной d-зоны в незаполненную. Ограничиваясь рассмотре­нием лишь одной незаполненной до конца d-зоны (имен­но так обстоит дело в случае Ni, Pd, Pt), выражение для Erdd(k) при принятых предположениях запишем в виде

1 ■ ід ^ ±1 п

1 4kdFk 2kdF — k\-

(2.50)

Здесь xd(EF) — плотность состояний реального металла на поверхности Ферми в d-зоне; UkdF — импульс Ферми d-электронов. Матричный элемент Mdd определяется пе­рекрытием волновых функций d-электронов решетки металла. Приближенно в интересующей нас области вол­новых чисел k—kF можно принять Мм2^. Необходи — 66
мо подчеркнуть, что точное выражение для Єг анизотроп­ного металла в пределе малых k дает именно плотность состояний на уровне Ферми. Эта плотность состояний введена в формулы (2.47) и (2.50), что означает факти­ческий учет анизотропии реального металла.

Для переходных металлов вклады еш и erds в ди­электрическую проницаемость ег малы — порядка не­скольких процентов, поэтому мы ими пренебрегаем. Для благородных металлов вклад erds существен н его можно оценить по формуле

где tiis — эффективная масса электронов проводимости; значения параметров /с и k& для Си, Ag, Аи можно най­ти в [2.8].

С учетом сказанного, подставляя асимптотическое значение еr{k) при й-мх> в выражение для экранирован­ного кулоновского потенциала, получаем

ф(г)=—е2г~1 ехр (—aR) cos (аR). ‘

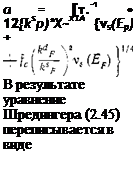Здесь R=2qsFr параметр а имеет вид ^

{ш*+т cos № + ■с)и № = °- (-53)

где через a=(kaF)~x обозначен второй существенный (наряду с а) параметр.

Итак, исходя из определенной модели электронной структуры металлов мы установили, что экранированный кулоновский потенциал зависит от двух безразмерных параметров а и а.

Плотности состояний брались из расчетов зонной структуры реальных анизотропных металлов. В тех слу­чаях, когда расчеты зонной структуры не вполне надеж­ны или отсутствуют, суммарная плотность состояний на­ходилась из электронной теплоемкости металлов, причем учитывались электрон-фононное и электрон-парамагнон — 5* 67

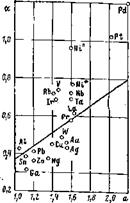
Рис. 2.9. Зависимость параметров а и а
для ряда металлов.

ное взаимодействия. Импульс Ферми электронов находился по формуле qiF= [Зл2,/П]|/3, где г, — число электронов в і-зоне; Q — объем элементарной ячейки.

В зависимости от отношения параметров а/а при решении уравнения Шредингера (2.53) реализуются две возможности. Количественный критерий, кото­рый позволял бы различать эти две возможности, можно полу­чить следующим образом.

Известно, что для данного потенциала Ф(я, a, R) существует критическое значение £кр параметра ; =

00

=JФ(a, a-, R)RdR, такое, что при ij<£Kp спектр являет-

0

ся сплошным. Используя результаты численного расчета

[2.9] , получаем ^ (а/а)^ = 0,362.

Таким образом, в координатах а, а существует кри­тическая линия — прямая. Все металлы, для которых па­раметры электронной структуры Vi (EF), k’F таковы, что а/а>0,362, относятся к первой группе. Они названы ка­тализаторами реакции. Металлы, для которых а/а< <0,362, относятся ко второй группе; они не являются катализаторами. Распределение металлов по группам показано на рис. 2.9. К первой группе относятся извест­ные катализаторы реакций гидрирования, такие как Pt, Pd, Ir, Rh, Ni. Качественно их принадлежность к этой группе определяется тем, что они имеют очень высокую плотность состояний на уровне Ферми в d-зоне а(Е) по сравнению с другими металлами.

Поскольку энергия связи атомов, молекул, твердых тел имеет электромагнитную природу, то подход к явле­ниям сорбции и катализа с точки зрения электромаг­нитных характеристик вещества (таких как диэлектри­ческая проницаемость) является правомочным и, по-ви­димому, перспективным.

Существуют такие параметры Vi(EF), k‘F, характерн­

ее

зующие электронную структуру реального металла, ко­торые позволяют в соответствии с принятым ранее опре­делением выявить металлы — катализаторы реакции окисления водорода.

Проведенный анализ явился лишь демонстрацией возможностей метода, поскольку не учитывалось суще­ствование поверхности, влияние электролита [в первом приближении это можно сделать, приняв, что влияние электролита и поверхности сводится к изменению пара­метров i(EF), k‘F в приповерхностном слое]. Очевидно, что отношение ajа зависит от потенциала электрода, типа электролита и как следствие от концентрации элек­тронов в приповерхностном слое.

Существенную роль на кинетику процесса оказывает экранирование поверхности. В рамках некоторых допу­щений показано, что понижение энергии активации из-за экранирования пропорционально параметру у:

Y = ____________________ (2 54)

1 1 + (2УЭф-/Эф)М^)/2 ‘ ‘

Здесь ‘s(Ef)—локальная плотность состояний

(ЛПС) в поверхностном узле і на поверхности Ферми;

vs(EF)=2ImG0(E—і’е, і, і) Iл; (2.55)

Go(E—і’є, і, і) —функция Грина невозмущенного метал­ла; Iэф и УЭф — эффективные параметры обмена и от­талкивания на узел с учетом корреляционных эффектов. В объеме металлов ЛПС совпадает с определенной ра­нее объемной ПЛОТНОСТЬЮ СОСТОЯНИЙ Vad(EF) и не зави­сит от положения узла І. Если узел і расположен на поверхности, ТО, вообще говоря, s(EF)^V, m{EF), В этом случае Vs (Ef) несет информацию как об электронном спектре всего металла, так и о локальных свойствах, вблизи поверхности, что снимает противоречие между «коллективным» и «локальным» подходами к поверхно­стным взаимодействиям. Однако с хорошей точностью можно оценить vs (Ef)^v05 (Ef) . Так как параметр Уэф. имеет порядок 1 эВ, а /Эф^0,6-^0,7 эВ, то у в основном определяется плотностью состояний на уровне Ферми,, что подтверждает результаты анализа. Экранирование — «металлическими», электронами влияет и на энергию — активации реакций переноса заряда на границе ме­талл— растворитель полярная жидкость. В результате-

экранирования энергия активации уменьшается, причем это уменьшение пропорционально параметру у. Физиче­ский смысл этого эффекта следующий. Поскольку сте­пени свободы растворителя образуют медленную подси­стему (см. выше), член в гамильтониане, ответственный за взаимодействие с быстрой подсистемой (электрона­ми), представляет собой статический одноэлектронный потенциал, зависящий от обобщенных координат медлен­ной подсистемы. Экранирование этого потенциала при движении медленной подсистемы приводит к некоторому изменению термов и уменьшению полной энергии акти­вации. Иными словами, электронная плотность подст­раивается под каждое новое положение медленной под­системы так, что изменение энергии быстрой подсисте­мы (электрон) при переходе медленной подсистемы (растворитель) к этому новому положению является минимальным.

Получить аналогичные соотношения для других рабо­чих компонент, более сложных, чем водород (кислород, углеводород, воздух и т. д.), пока еще не представляется возможным.

Комментарии запрещены.