Бурение грунтовых зондов, установка энергетических колодцев

При моделюванні використовується загальноприйнятий під­хід, який був викладений в огляді на окремі випадки, приведені в першому розділі. Загальна ідея підходу полягає в тому, що зміна всіх основних параметрів органічного середовища пропорційна ма­сі ні] мікроорганізмів, життєдіяльність яких є такою, що визначає решту всіх процесів. Коефіцієнти пропорційності залежать від ста­ну або параметрів середовища. Ці коефіцієнти представляються на — півемпіричними формулами, і вхідні параметри визначаються екс­периментально [18, 67].

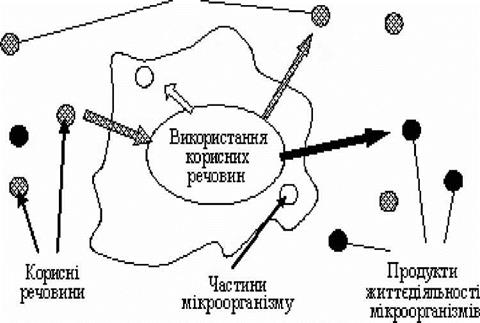
У даній системі протікають три основних і відмінних один від одного процесів: процес споживання живильних речовин мікроор­ганізмами, розмноження мікроорганізмів і відмирання мікрооргані­змів. Під час протікання цих процесів утворюється газ, деякі тверді продукти життєдіяльності мікроорганізмів і виділяється або погли­нається теплова енергія. При цьому присутні деякі нейтральні ре­човини, які часто несуть деяку функцію, наприклад, вода, як сере­довище, в якому відбуваються хімічні реакції. На рис. 3.6 приво­диться загально-схематична картина складових процесу споживан­ня живильних речовин мікроорганізмами.

Рисунок 3.6 — Споживання живильних речовин мікроорганізмами [67]. Взагалі кажучи, це є "виробничим процесом", в якому живи­льні речовини переробляються в ряд продуктів. Структура взаємодії окремих складових цієї системи і проце­сів, що протікають в них, приводиться на рис. 3.7.

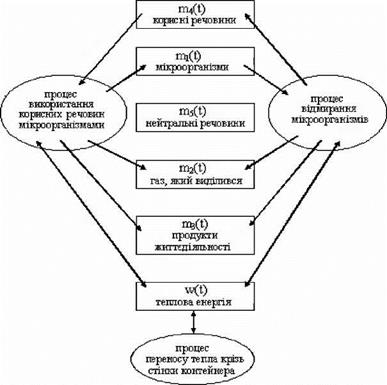
Рисунок 3.7 — Структурна схема взаємодії складових органічного сере­довища і процесів, що протікають в них (стрілками позначені процеси пере­дачі матеріальних речовин і теплової енергії)

Використовуючи структурну [67, 212] схему взаємодії і при­йнятий загальний підхід моделювання в біологічних системах, за­пишемо рівняння для визначення мас ті, т2, т3, т4 і тепла w, які виділяються у виробничому процесі:

dmi/dt=kai mi-кы mi	m1(0)=m10;	(3.21)
dm2/dt=ka2 mi+kb2	m2(0)=m20;	(3.22)
dm3/dt=ka3 mi+kb3 mb	m3(0)=m30;	(3.23)
dm4/dt=kb4 m!-ka4 mb	m4(0)=m40;	(3.24)
dw/dt=ka5 mi+kb5 m1+6(Tn-T)S,	w(0)=w0,	(3.25)

де t — час,

тю, т2о, т30, т40, wo — початкові значення величин mi, m2, т3, т4, w, відповідно.

Прирости всіх складових системи в одиницю часу пропорційні масі мікроорганізмів т1; оскільки саме їх життєдіяльність і є осно­вною причиною всіх змін в органічному середовищі, яке ми розгля­даємо. Це є загально прийнятим в науковій літературі. Коефіцієнти пропорційності змінні, залежать від стану системи, і деякі можуть міняти свій знак. Ця змінність знаку пов’язана з процесами роз­множення і відмирання. Тому вони розбиті на дві частини. Коефіці­єнти розмноження ка1, ка2, ка3, ка4, ка5 і коефіцієнти, пов’язані з від­миранням kbl, kb2, kb3, kb4, kb5. І всі коефіцієнти kal, ka2, ka3, ka4, ka5 кьь kb2, kb3, kb4, kb5 однакової розмірності (1/час) і при цьому коефі­цієнти kal, ка2, ка3, ка4, кьі, кЬ2, кьз, кЬ4 є ненегативними, тобто:

каі >0, ка2 >0, ка3>0, ка4>0 (3.26)

кЬі>0, кЬ2>0, кьз>0, кЬ4>0 (3.27)

Величини dmn/dt, п=1, 2, 3, 4 представляють зміну мас в оди­ницю часу.

Даний процес протікає в замкнутому об’ємі і має місце закон збереження мас. Процеси, що протікають в мікроорганізмах, при­ймемо миттєвими, без запізнювання. Живильні речовини, поглине­ні в одиницю часу мікроорганізмами, в туж мить переробляються, приводять до збільшення у вазі, тобто розмноженню, перетворю­ються на газ, і інші продукти життєдіяльності мікроорганізмів в ту ж одиницю часу.

kai(t) m1(t)+ka2(t)m1(t)+ka3(t)m1(t)=ka4(t)m1 (t)

kai +ka2 +ka3 =ka4

Звідси слідує

kai/ka4 +ka2 /ka4+ka3/ka4=l;

kai/ka4=kan; (3.28)

ka2/ka4 ka2i,

ka3/ka4=ka3i.

Приймемо, що мікроорганізми даного типу споживають тільки один вид живильних речовин, тому з однієї і тієї ж кількості живи­льних речовин в процесі їх споживання мікроорганізмами виділя­ються складові однієї і тієї ж кількості відповідно незалежно від внутрішнього стану середовища і мікроорганізмів. Якщо маса жи­вильних речовин зміниться в N разів, то решта всіх компонентів зміниться в N разів, тобто вони утворюють вектор з пропорційними компонентами [53]. Тоді з рівнянь (2.8) отримаємо:

kal(t) kaii ka4(t),

ka2(t) =ka21ka4(t); (3.29)

каз(0 каз ika4(t),

ka5(t) ka51 ka4(t),

де кац, ka2i, ka31 ka5i — постійні для даного типу мікроорганізмів і даного типу живильних речовин коефіцієнти пропорційності, які є позитивними і безрозмірними.

Процес в органічному середовищі є деяким виробничим про­цесом, при якому споживаються живильні речовини, і в результаті утворюються деякі нові продукти: мікроорганізми, гази і ін. проду­кти життєдіяльності мікроорганізмів [67, 212]. Тут основною поча­тковою сировиною є живильні речовини. Враховуючи це, виділені окремо живильні речовини і відповідно коефіцієнт ка4. Коефіцієнти каі, ка2, ка3, ка5 змінюються пропорційно коефіцієнту ка4 або всі кое­фіцієнти змінюються пропорційно друг другу.

В принципі може бути виділений будь-який з коефіцієнтів ка1, ка2, ка3, ка5. Наприклад, якщо виділити коефіцієнт ка1, який оцінює швидкість розмноження мікроорганізмів, то з (1.9) отримаємо:

ка2= (ка2і/кац)каі

каз=(каз і/ка і і)каі

ка4=(1/каіі)каі (3.30)

ка5=(ка51 /каі і)каі

Представляє інтерес виділення коефіцієнта ка2, оскільки кіль­кість газів, що виділяється, виміряти дещо простіше. В цьому випа­дку залежності запишуться у вигляді:

kai=(kai i/ka2 i)ka2

каз=(ка3 i/ka2 i)ka2 (3.31)

ka4=(l/ka2i)ka2

ka5=(ka5 i/ka2 i)ka2

Рівняння (3.28)-(3.31) описують структурну залежність проце­су життєдіяльності мікроорганізмів. Структура процесу характери­зується безрозмірними коефіцієнтами кац, ка2і, казь ка5і. Якщо структура процесу задана, то п’ять коефіцієнтів ка1, ка2, ка3, ка4 ка5 зв’язані чотирма співвідношеннями, представленими в одному з видів (3.29), (3.30) або (3.31). Досить визначити тільки один з кое­фіцієнтів, а інші можна обчислити за цими формулами.

Крім того, в кожну одиницю часу виконується закон збере­ження маси, який запишемо в наступному вигляді:

Співвідношення (3.34) накладає додаткову умову на коефіціє­нти пропорційності, що визначають структуру процесу.

Введені коефіцієнти системи визначаються експериментально, але отримані для них співвідношення виконуються, оскільки вони отримані на основі фундаментального закону — закону збереження мас. Порушення їх приведе до порушення закону збереження. Точ­ність їх виконання залежить від точності вимірювання при експе­рименті. Коефіцієнти кац, ка2Ь казі, ка5і, 1 визначають співвідно­шення між компонентами, що утворюються, при переробці живи­льних речовин. Вони визначаються типом мікроорганізмів, типом живильних речовин і вважаються постійними для кожного типу мі­кроорганізмів і типу живильних речовин, а також не залежними від зовнішніх чинників. Зовнішні чинники впливають тільки на коефі­цієнти каі, ка2, кдз, ка4, ка5, які задовольняють лінійним співвідно­шенням (3.29)-(3.31) і поводяться пропорційно. Якщо, наприклад, каі лінійно залежить від якогось параметра, то решта всіх коефіціє­нтів, ка2, кдз, ка4, ка5, також лінійно залежать від цього параметра.

Важливим параметром є швидкість росту популяції мікроор­ганізмів ка] і залежність її від різних чинників. Для розвитку попу­
ляції коефіцієнт kal повинен бути додатнім. Численні експерименти показують, що параметр ка1 при низьких для даного виду мікроор­ганізмів температурах дуже малий, мікроорганізми не розмножу­ються. І лише досягнувши деякого значення температури середо­вища коефіцієнт ка1 починає зростати, і при подальшому її підви­щенні продовжує своє зростання, досягає максимуму і потім почи­нає убувати [53, 54, 55, 56, 57, 58].

Аналогічно розмноженню розглянемо процес відмирання мік­роорганізмів. Приймемо процес миттєвими, без запізнювання. Час­тина маси відмерлих мікроорганізмів надалі споживається як живи­льні речовини, частина переходить в гази і ін. продукти життєдія­льності мікроорганізмів, утворюється і теплова енергія (рис. 3.7). Мікроорганізми, які відмирають, вважаються в середньому однорі­дними і розкладаються на пропорційні частини. Якщо маса відмер­лих мікроорганізмів зміниться в N разів, то маса кожної компонен­ти зміниться в N разів, тобто вони утворюють вектор з пропорцій­ними компонентами [59, 60]. Зміна мас в одиницю часу kbnmb п=1, 2, 3, 4 і кількість тепла кЬ5ПТ|, що виділяється при відмиранні мікро­організмів за одиницю часу, задовольняють пропорції:

((kbimi)/l)=((kb2mi)/kb2i)=((kb3mi)/kb3i)=((kb5mi)/kb5i)=((kb4mi)/kb4i) (3.35)

де кЬц, kb2i, kb3i, kb5i — коефіцієнти пропорційності, які є позитивними і безрозмірними.

Звідки витікає, що

kb2 — kb2ikbikb3 — kb3ikbi

кы — kb4ikbi kb5 — kb5ikbi

У кожну одиницю часу виконується закон збереження маси:

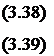kb2mi(t) + kb3mi(t) + kb4mi(t) — kbimi(t) = 0

Звідки слідує рівняння:

kb2+ kb3 + kb4 — kbi kbn+ kb2i+ kb33-l

По заданому значенню коефіцієнта kbl, при відомій структурі процесу (тобто коефіцієнтах kb2i kb31 kb41 kb51) решта всіх коефіцієн­тів визначається згідно рівняння (3.36).

Враховуючи, що

w = стТ,

де с-теплоємність, m — маса, що нагрівається,

Т — температура,

а також введені вище позначення, рівняння (3.21)-(3.25) запишуться у вигляді:

dmj/dt = kai |1<а4ітіі — kblmb т!(0)=т10; (3.40)

dm2/dt = ka2i ka4mi + kb2ikbimi т2(0)=т2о; (3.41)

dm3/dt = ka31ka4 m, + kb31kblm! m3(0)=m3O; (3.42)

dm4/dt = kb4ikbiiiii — ka4mb m4(0)=m0; (3.43)

dcmT/dt = ka5|ka4m| + к^кыпц + 6(Tn-T)S, T (0)=Tou, (4.44)

де Too — початкове значення температури.

Коли контейнер закритий наглухо, маса, що нагрівається, не міняється і дорівнює початковому значенню:

m = m0 = const. (3.45)

Якщо контейнер також закритий, але газ, що утворився в кон­тейнері, безперервно відводиться, маса в контейнері в даний мо­мент часу зменшується на величину маси газу т2. Тому в рівнянні (2.24) маса т дорівнює:

т = т0 — т2. (3.46)

Отримані рівняння адекватно враховують структуру процесів що мають місце в популяції одного виду мікроорганізмів. Дозволя­ють зрозуміти, що при цьому відбувається, як взаємодіють окремі частини системи, якими параметрами характеризуються протікаючі процеси. Тут отримані і введені ті параметри, які характеризують процес в цілому, а також і його структуру. Це є основою для мето­дично правильної постановки експериментів і обробки їх результа­тів.

На основі аналізу експериментальних даних коефіцієнт каї приблизно апроксимується наступною залежністю [61, 62]:

kai = kal(T, pH, m4/V, m3/V) = ка1ор1фа(Т)са(рН)ма(т4/У)за(т3/У) (3.47)

де kaiopt — максимальне значення коефіцієнта каЬ що досягається при T=T0pt, pH=pHoPt і надлишку живильних і мінімумі отруйливих речовин.

Функції фа(Т) і са(рН) апроксимуються наступними виразами:

°Д<Тті„

(T-T )-(Т-Т ■ )2

ф (T) =———————————— ^———————————————— ,Т <Т<Т (3.48)

(Торі — тті„ ) • [(Topt — Tmill) ■ (Т — Topt) — (Topt — Tmas ) . (Topt + TnAl — 2T) mm

0,T>Tmas

де T — температура середовища,

Tmin — значення температури нижче за яку зростання популяції не від­бувається,

Ттах — значення температури вище за яку зростання популяції не відбу­вається.

Отже розвиток популяції розглядається на відрізку Tmin<T<Tmax. Аналогічно величини pHmin і рНтах визначаються з умови ca(pH<pHmin) = ca(pH>pHmax) = 0.

Функція м(ш4/У) апроксимується рівнянням Моно [63]:

ма(ш4/V) = (ш4/V)/((m4/V)+Ks) (3.50)

де m4/V — концентрація живильних речовин;

V — об’єм контейнера;

Ks — так звана константа насичення: концентрація живильних речо­вин при якій спостерігається половинна швидкість росту в порівнянні з шви­дкістю росту при надлишку живильних речовин.

Функція за(ш3/У) апроксимується рівнянням Ієрусалимського

[64]:

з(,(т3Л’НК"У((тзЛ’),,+К") (3.51)

Формула (3.51) визначає швидкості росту популяції залежно від впливу на процес життєдіяльності отруйливих речовин. Тут п —

деякий коефіцієнт, що вносить нелінійність, Кі — концентрація от­руйливих речовин при якій швидкість росту зменшується удвічі, (m3/Y) — концентрація отруйливих речовин.

Коефіцієнт kbl приблизно апроксимується залежністю:

кЬі=кЬі(Т)=кЬІ0р1фь(Т) (3.52)

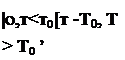Згідно експериментам [61,66], залежність коефіцієнта kb] від температури середовища лінійна:

де Т0 — температура при якій фь(Т)=0.

Комментарии запрещены.