Бурение грунтовых зондов, установка энергетических колодцев

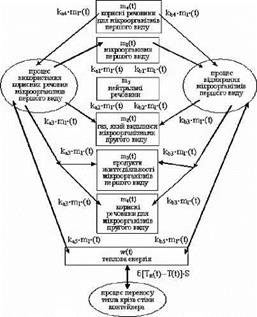
Як показують експерименти [67, 68, 69], в даному об’ємі мік­роорганізми певного вигляду припиняють своє існування з різних причин, в основному за рахунок витрачення живильних для нього речовин. Але продукти їх життєдіяльності є живильними для інших видів мікроорганізмів. В результаті починають розвиватися мікро­організми іншого вигляду. Утворюється складний симбіоз різних мікроорганізмів. Розглянемо механізм взаємодії і сумісного розвит­ку двох видів мікроорганізмів. Процес життєдіяльності кожного з мікроорганізмів має ту ж структуру що і у разі мікроорганізмів од­ного вигляду за винятком того, що тепер додається процес їх взає­модії. Частина продуктів життєдіяльності мікроорганізмів першого вигляду є живильною для мікроорганізмів другого вигляду [67]. Структура процесів, що протікають в популяції мікроорганізмів першого вигляду, представлена на рис. 3.8.

Рисунок 3.8 — Структурна схема взаємодії складових органічного сере­довища і процесів, що протікають в них в результаті життєдіяльності мікро­організмів першого вигляду і процесу перенесення тепла через стінки кон­тейнера

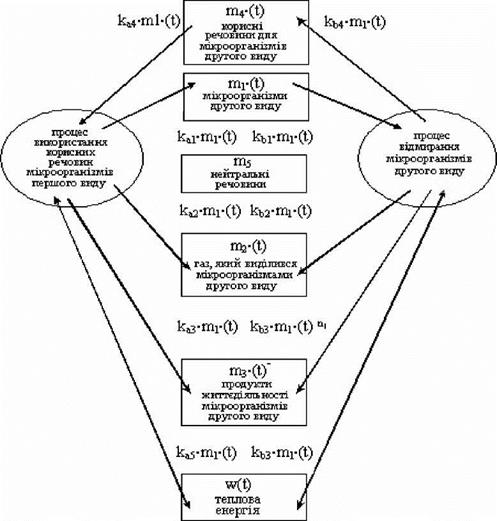
Структура життєдіяльності мікроорганізмів другого вигляду представлена на рис. 3.9.

Рисунок 3.9 — Структурна схема взаємодії складових органічного сере­довища і процесів, що протікають в них в результаті життєдіяльності мікро­організмів другого вигляду

Тут для величин використовуються ті ж позначення, які були введені в розділі 3.42. Але для величин тих, що описують мікроор­ганізми другого вигляду введений верхній індекс (*). Наприклад, іП|*, т2*, т3*, т4* — маси відповідних компонент органічного сере­довища для мікроорганізмів другого вигляду. Для величин мікроор — ганизмів першого вигляду збережені позначення без змін, без верх­нього індексу.

Використовуючи схеми структур взаємодії різних компонент популяцій мікроорганізмів, приведених на рисунках (3.7) і (3.8), складемо систему рівнянь розвитку мікроорганізмів у вигляді:

dmi/dt = ка|ітіі — кьііиі,	mi(0)=mio;	(3.57)
dm2/dt = ка2иіі — кЬ2ть	m2(0)=m2o;	(3.58)
dm3/dt = ка3ті — кьзть	т3(0)=т30;	(3.59)
dm4/dt = ка4иі] — ка4ть	m4(0)=m40;	(3.60)
dm і / dt = каі*ті* — кыТпД	mi*(0)=mio*;	(3.61)
dm27dt = ка2*ііі|* — кЬ2*гпі*,	m2*(0)=m2o*;	(3.62)
dm37dt = ка3 іті, * — кЬз*тЛ	m3*(0)=m3o*;	(3.63)
= kb4*mi*- ка4*т і%каз"т і+кьз"т и	m4*(0)=m4o*;	(3.64)
ка5ті + кЬ5ті + ка5*ті*+ кЬ5*ті%	6(Tn-T)S, w(0)=w0;	(3.65)
w = с-т-Т;		(3.66)
m = иіі + ліз+ m4 + иіі*+ m3*+ m4*+ m5;	(3.67)
пн + ВЦ + тз + m4 + mi*+ m2*+ m3 + m4*+ 1Ц5 = const.	(3.68)

Для кожної складової мас має місце закон збереження. Зміна мас компонент органічного середовища в одиницю часу кшШі, п=1, 2, 3, 4 і кількість тепла ка5Ші, що виділяється мікроорганізмами за одиницю часу, задовольняють пропорції:

(ка іиі! )/ка!!=(ка2іті! )/ка21 =(казШ і )/казі =(казШі )/казі=(ка5ті )/ка5і=(ка4ті)/1, (3.69)

де кап, ка2і, каЗЬ ка4ь ка5] — коефіцієнти пропорційності, які є постійни­ми, позитивними і безрозмірними.

Тут ka3rri|(t) частина продуктів життєдіяльності мікроорганіз­мів першого вигляду, яка є живильною для мікроорганізмів другого вигляду, а казні] (t) — частина продуктів життєдіяльності мікроорга­нізмів першого вигляду не є живильною для мікроорганізмів друго­го вигляду.

З цих пропорцій слідує співвідношення:

ка] каі іка4, ка2 ка2іка4,

ка3ґ = ка3іґ ка4, (3.70)

ka3S = ka3iS ка4,

ка5 ка5іка4,

які іноді зручно представити у вигляді:

ка2 = (ка2і/к] [) каЬ ка3ґ = (казіґ/кц) каЬ

ka3S = (ka31S/k11)kab (3.71)

ка4= (1/кц) каЬ

ка5 = (ка5]/кц) ка1,

Коефіцієнт каі залежить від температури і pH середовища і ви­значається по формулі (3.47).

Закон збереження мас для процесу споживання живильних ре­човин мікроорганізмами першого вигляду запишеться у вигляді:

kaimi(t) + ka2inі(t) + ka3nni(t) + ka3Smi(t) — ka4nii(t) = 0. (3.72)

Звідки слідує:

kai + ka2 + ка3ґ + ka3S = — ka4. (3.7 3)

Причому по фізичному сенсу всі коефіцієнти не негативні:

каі>0, ка2>0, ка3ґ>0, ka3S>0, ка4>0 (3.74)

Аналогічно для коефіцієнтів кьг, кьзґ, kb3S, kb4., кЬ5і отримаємо залежності:

кЬ2= кьгікьь кьзґ = кЬЗіґкьь

кЬз^ = kb3iSkbb (3-75)

kb4= кмі^ь

кЬ5= кьбікьь

де кЬ2і, кЬЗіґ, kb3]S, 1<Ы1, kb5i — ненегативні постійні коефіцієнти, залежні від виду мікроорганізмів.

Коефіцієнт kbi залежить від температури середовища, концен­трації отруйливих речовин і визначається по формулі (3.51).

Закон збереження мас для процесу відмирання мікроорганіз­мів першого вигляду запишеться у вигляді:

kb2mi(t) + kb3rmi(t) + kb3Smi(t) + kb4mi(t) — kbimi(t) = 0. (3.76)

Звідси слід:

к Ъ2 + кьзґ + kb3S + къ4 —к ы. (3.7 7)

При цьому по фізичному сенсу:

кы>0, къ2>0, кьзґ>0, 1<ьз8>0, 1<ь4>0. (3.78)

Розглянемо тепер закон збереження мас для процесу спожи­вання живильних речовин мікроорганізмами другого вигляду і умову пропорційності компонент мас і кількості теплової енергії, що виділяється, мікроорганізмами в одиницю часу. В результаті отримаємо залежності:

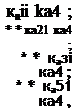
(3.79)

де кап*, ка2і*, казі*, ка5і* — ненегативні постійні коефіцієнти, залежні від виду мікроорганізмів.

Рівняння (3.79) перепишемо у вигляді:

ка2 = (ка21 /кац )каі, каЗ = (каЗІ /кац )каі,

ка4* = (1/каіі>аь (3.80)

ка5 (ka5l kail )kal,

Закон збереження мас для процесу споживання живильних ре­човин мікроорганізмами другого вигляду запишеться у вигляді:

kaiW(t) ka2W(t) + ka3in I (t) — ka4W(t) = 0. (3.81)

Звідки витікає, що:

kai*+ ка2*+ каЗ*= — ка4.

При цьому по фізичному сенсу:

ка1*>0, ка2*>0, ка3*>0, 1<а4*>0.

Закон збереження мас для процесу відмирання мікроорганіз­мів другого вигляду і умова пропорційності компонент мас і кіль­
кості, що виділяється тепловій енергії мікроорганізмами другого вигляду в одиницю часу приводить до залежностей:

kb2*=kb2i*kbi*, кЬз* =kb31*kbl*,

kb4* =kb4i*kbi*, (3.82)

kb5* =kb5i*kbi*,

де kb2i*, kb3i*, kb4|*, kb5i* — ненегативні постійні коефіцієнти, залежні від виду мікроорганізмів.

Закон збереження мас для процесу відмирання мікроорганіз­мів другого вигляду запишеться у вигляді:

kb2*mi*(t) + kb3*m|*(t) + kM*mi*(t) — kbl*m!*(t) = 0.

Тоді отримаємо

kb2* + kb3* + kb4* = — kbl*.

При цьому по фізичному сенсу:

kbi*>0, kb2*>0, kb3*>0, kb4*>0.

З урахуванням всього вище приведеного рівняння динаміки розвитку різних компонент мас запишуться в наступному вигляді:

dmi/dt = ka| 11<а4іп і — кьіть (3.83)

dm2/dt = ка2|ка4т| + кЬ21кЬіть (3.84)

dm3/dt = ка31 ка4т! + ка31 кьіть (3.85)

dm4/dt = kb4i кЬііНі — ка4ті; (3.86)

dmi*/dt = кац*ка4*ті* — кЬ2і*ті*; (3.87)

dm2*/dt = к^і* ка4*ті* + kb2i*kbi*mi*; (3.88)

dm3*/dt = ка3і*ка4*ті* + кЬЗі*кЬі*ті*; (3.89)

dm4*/dt = кЬ4*іН] * — ка4*іП | * + ка3 ка4ті + ка3 ка4ті; (3.90)

dcmT/dt = ka5ika4mi+kb5]kbimi+ka5i*ka4*mi*+ka5i*kbi*mi*+6(Tn-T)S. (3.91)

Отримані рівняння дають узагальнення великої кількості експери­ментальних досліджень, які опубліковані в монографіях, підручни­ках і журнальних статтях, наприклад, в роботах [70, 71, 72]. Резуль­тати, отримані експериментально є важливими, представляють ос­нову математичного моделювання, викладеного в цій роботі, але вони не описують динаміку процесу і взаємодії окремих складових популяції.

Коефіцієнти системи рівнянь (3.83)-(2.91) визначаються фор­мулами (3.47)-(3.53), (3.70)-(3.81) отриманими експериментально. Але у разі складених процесів приймемо, що тільки частина живи­льних речовин другого виду мікроорганізмів впливає на pH. Рів­няння (3.54) тоді запишеться у вигляді:

pH = (рН0 + ai*(mp*/V))/(l + а2*( mp*/V)), (3.92)

де рН0 — pH середовища без речовин, що змінюють його;

тр* — маса змінюючих pH речовин в середовищі, тобто маса частини живильних речовин другого виду мікроорганізмів змінюючого pH середови­ща;

V — об’єм середовища;

аі*, а2* — деякі коефіцієнти визначувані експериментально; pH — реальний pH середовища.

Приймемо, що частка змінюючих pH речовин серед живиль­них речовин другого виду мікроорганізмів постійна і маса цих ре­човин обчислюється за наступною формулою:

mp* = kp*m4*, (3.93)

де иіз — маса продуктів життєдіяльності мікроорганізмів;

кр* — коефіцієнт пропорційності характеризує частку змінюючих pH речовин в продуктах життєдіяльності мікроорганізмів;

тр* — маса частини продуктів життєдіяльності мікроорганізмів тих, що змінюють pH середовища.

Тоді рівняння (3.92) запишеться у вигляді:

pH = (рНо* + 6|*(m47V))/(l + 62*(m47v)), (3.94)

де 6j кр з.} ,

б2 =кр а2

Формула (3.94) визначає залежність pH від продуктів життєді­яльності мікроорганізмів.

Проведемо деякі спрощення цих моделей. Введемо наступні коефіцієнти:

ki= ka] [ka4i — kbl;
кг = кагіка4 mi — кьгікьь
кз = ka3ika4 — кьзікьь
к4 = ка4іка4- кь4]кы;
k/ = kallV+kb]l*kbi;
кг* = кагі *ka4*+kb21*kbl;
кз*=каз;ка;+кьз;кьі;

sjc sjc II!!

к4 — кЬ4 — ка4 + каз ка4 + ка3 ка4,

кб = ка5іка4 +kb51kbi + ка51 ка4 +kb51kbl. (3.95)

Тоді система (2.63) — (2.71) розвитку складених процесів за­пишеться:

для мікроорганізмів першого виду

dmi/dt = kiinb	mi(O) = mm,	(3.96)
dm2/dt = к2шь	m2(0) = m20,	(3.97)
dm3/d = к3іпі — dm4 /dt,	m3(0) = m30,	(3.98)
dm4/dt = — к4іпь	m4(0) = m40,	(3.99)
для мікроорганізмів другого вигляду
dm 17dt = 1< і *m і*,	mi*(0) = іпю	(3.100)
dm27dt = 1<2*ГП|*,	m2*(0) = m20*,	(3.101)
* * dm3 /dt = k3 mb	m3*(0) = m3o*,	(3.102)
* * dm4 /dt = 1<4 mb	m4*(0) = m40*,	(3.103)

для теплової енергії і закону збереження мас системи

dcmT/dt = k5iiii + k5*m, * + 6(Tn-T)S, T(0) = T0; (3.104)

m = mi + m3 +m4 + пі] * +m3* + m4* + m5; (3.105)

^ ^ ^

пі! + m2 + m3 +1114+111! + m2 + m3 + m4 + m5 = const. (3.106)

Взагалі кажучи, як показують експериментальні дані, зазви­чай, виходить складний симбіоз мікроорганізмів різних видів. Ви­ділення першого і другого виду мікроорганізмів можуть викорис­товуватися мікроорганізмами третього вигляду і т. д. Виходить складна система взаємозв’язаних популяцій і процесів життєдіяль­ності різних видів мікроорганізмів. Це дуже складний вид процесів. Вище приведений лише один з можливих підходів математичного моделювання таких процесів.

Комментарии запрещены.