Бурение грунтовых зондов, установка энергетических колодцев

Мікроорганізми багато чисельні й різноманітніші чим тварин­ний світ. З огляду їх великого впливу на життєдіяльність на Землі вивченню мікроорганізмів присвячене величезне число експериме­нтальних і теоретичних досліджень. З’ясований істотний вплив на їхнє розмноження й загибель ряду параметрів стану середовища. Наприклад, найбільш важливими параметрами середовища є: тем­пература, їжа, кислотність середовища, концентрації молекулярно­го кисню, вологість середовища й ряд інших параметрів. Але ці па­раметри для різних організмів різні. Наприклад, стосовно концент­рації молекулярного кисню в середовищі виділяють:

— облигатні аероби — для здійснення процесів метаболізму потребують молекулярного кисню;

— облигатні анаероби — не використовують молекулярний кисень, більше того, він для них токсичний;

— факультативні анаероби — можуть жити як при наявності, так і у відсу­тності кисню.

У своїй життєдіяльності мікроорганізми споживають живильні речовини, енергію, перетворюють їх і в результаті виділяють про­дукти своєї життєдіяльності. Залежно від виду мікроорганізмів змі­нюється й набір живильних для нього речовин. Виділення одних організмів можуть бути живильними для інших.

На жаль, у теперішній час статистичні дані про вплив різних параметрів середовища на життєдіяльність мікроорганізмів явля­ються розкиданими, важко встановити узагальнені критерії й мало надійних математичних моделей. Хоча, звичайно, ці дослідження присвячені вивченню конкретного виду мікроорганізмів, але не є досить повними, щоб провести ідентифікацію параметрів моделі. Як відзначають [43, 44, 4], принципова трудність полягає ще в то­му, що не існує систематичних правил висновку самих рівнянь. Процедури їх складання ґрунтуються на напівемпіричних законо­мірностях, правдоподібних міркуваннях, аналогіях і мистецтві мо­делюючого. Технічні труднощі пов’язані з високою розмірністю за­вдань по моделюванню співтовариств.

Коротко розглянемо стан досліджень мікроорганізмів і їх мо­делей. Зображення росту популяції (або зміни концентрації біома­
си) розглянуто моделлю Друпа [43, 44], рівняння (3.11), тобто при-

dB

ріст популяції в одиницю часу — вважається пропорційним кіль-

dt

кості організмів В у популяції і у теперішній час є загальноприйня­тим. В даному випадку величина В вимірює кількість, масу або

• • dB _

концентрацію організмів, — — зміна кількості в одиницю часу. У

dt

цієї моделях уся проблема зводиться до оцінки коефіцієнта пропо­рційності, який для різних видів організмів визначається експери­ментально.

Наприклад, у роботах [45] приводяться деякі експерименталь­ні результати і їх аналітична вистава. Коефіцієнт пропорційності росту залежно від температури й значення pH середовища запису­ється у вигляді:

Вшах = Вшах (Т, РН) = Bopt ^ (Т) ‘ Р (РН) (3‘13)

де jLiopt — максимальне значення коефіцієнту цтах, що досягається при

T = ToPt і РН=РН0РІ,

функції т(Т) і р(рН) апроксимується наступними виразами:

/ ч (т-т )-(Т-Т. )2

(т — Т. УГ(т — Т. У(т-т Д-(т — Т )-(т t+T. -2-т)1’

opt mm / |_ opt mm / у opt / opt max / opt mm /J| 14^)

(pH — pHmin) • (pH — PHmax )

(pH — pHmin) • (pH — PHmax ) — (pH — pH opt)

pHmin<pH<pHmax,

де T — температура середовища,

Tmm — значення температури нижче якої росту популяції не відбувається, Тщах — значення температури вище якої росту популяції не відбувається. Так що розвиток популяції розглядається на відрізку Tmin<T<Tmax. Аналогічно величини рН1піп і рНтахвизначаються з умови р • (pH < pHmin) = р • (pH > рНтах) = 0.

Нижче на рис. 3.1 та 3.2 наведені графіки розрахунків по фо­рмулах (3.13)-(3.15).

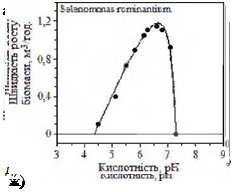
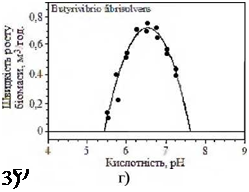
На рисунку 3.3 приводяться точки експериментальних даних з накладеними розрахунковими кривими, отриманими в роботі [46] для бактерій Butyrivibrio fibrisolvens, Brucella melitensis, Listeria monocytogenes, Megasphaera elsdenii, Propionibacterium acnes, Streptococcus bovis, Selenomonas ruminantium.

Традиційний шлях вивчення співтовариств мікроорганізмів полягає в моделюванні безперервних культур. Загальне рівняння, що описує кінетику концентрації кліток у такому процесі, має ви­гляд

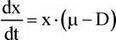
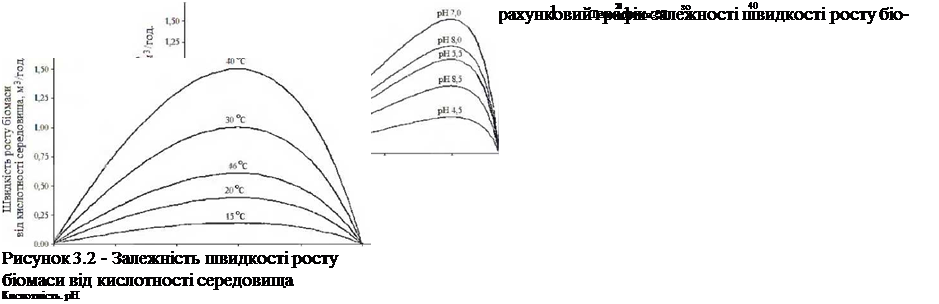
(3.16)

де х — концентрація кліток у культиваторі, ц — функція, що описує роз­множення популяції, D — швидкість вимивання.

Швидкість розмноження може залежати від концентрації клі­ток, концентрації субстрату s, температури, pH середовища й інших факторів [46, 47, 48].

а, б, в, г, д, е, ж, з — для різних видів бактерій, назва яких вказана у верхній частині графіків

Рисунок 3.3 — Швидкості росту бактерій в залежності від кислотності середо­вища

У мікробіологічних системах, як правило, швидкість росту лі­мітується концентрацією субстрату, що відбивається залежністю, запропонованою Ж. Моно [49]:

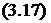Urn’S

Ks + s ’

де jLim — максимальна швидкість росту організмів за даних умов, Ks — специфічна константа, чисельно рівна концентрації субстрату, при якій шви­дкість росту культури дорівнює половині максимальної (константа напівна- сичення).

Модель росту мікробних популяцій [50], що описує концент­рацію мікробної біомаси (х) і концентрацію субстрату, що лімітує (s) в умовах хемостатного культивування, записується у вигляді

dx _ dxt dxp dt dt dt

ds dt

де Xp — концентрація мікроорганізмів у приймачі, куди зливається наро­стаюча бактеріальна суспензія;

Хт — сумарна концентрація мікроорганізмів (хт=х+хр); ц — питома швидкість росту визначається по формулі (6), s — концентрація ресурсу, що лімітує, у середовищі;

Ks — константа напівнасичення при лімітуванні даним субстратом;

So — величина концентрації субстрату, що лімітує, на вході в культива­тор;

D — швидкість розведення, рівна відношенню швидкості вступу живи­льного середовища до обсягу культури;

Y — економічний коефіцієнт (вихід біомаси на одиницю спожитого суб­страту).

Принциповою особливістю даної відкритої системи є можли­вість установлення динамічної рівноваги. В установленому стані ц = D, а Х0 = Y • (s — s0), Х0, s0 — постійні значення, відповідні до ста­ціонарного стану. На основі модифікації цієї моделі розглядаються різні методи проточного культивування динаміки концентрації біо­маси мікроорганізмів. Наприклад, хемостат з поверненням, безпе­рервне культивування без виносу мікробних кліток, періодична ку­льтура з підживленням, періодична культура з газовим харчуван­
ням, проточний реактор з іммобілізованими клітками. Використан­ня в математичних моделях залежності швидкості росту популяції як функції одного елемента живлення JLl(s) припустиме тільки для

систем з встановленим характером лімітування. Однак, зміна фак­торів лімітування зустрічається повсюдно й представляє як теоре­тичний, так і практичний інтерес. Існує кілька різних підходів до теоретичного опису механізму зміни факторів, що лімітують ріст популяції. Найпоширенішими є моделі, у яких передбачається, що в будь-який момент часу ріст контролюється тільки одним елементом живлення. Однією з областей застосування диференціальних рів­нянь у моделюванні мікробіологічних співтовариств є аналіз мож­ливих стаціонарних станів змішаної культури. Наприклад, дослі­дження І. Р. Співака і Дж. С. Рокема [51], у якій вивчалася взаємодія двох видів гетеротрофних бактерій, що конкурують за проміжні по­заклітинні метаболіти, виділювані бактеріями — метилотрофами.

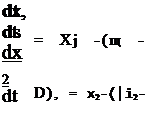Система рівнянь, що описує таке співтовариство, містить у со­бі вираження для динаміки бактеріальних біомас, концентрації кис­ню, метанолу, етанолу, ацетату у ферментаційнім рідкім середови­щі:

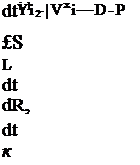ГГ Y. j

Питома швидкість росту видів задається формулами:

йі = min {pml, pu ■ Sj} ■ (1 — Pmli ■ Px) ■ • (1 — Pm4i • Pj),

fl2 = min {рт2,Рн ‘ si 5P23 ‘ P3 + P24 ‘ P4 } ‘ (i _ Pm2i ‘ Pi ) ‘ (i _ Pm22 ‘ ^2 ) ’

Ш = тІП {Ртз, Pli • Si; Рзз • P3 + Р34 • P4 } • (1 — РтЗІ ‘ P1)‘ {l ~ Pm32 ‘ P2 ) ■

Швидкість споживання субстрату може бути представлена як

_ Pij щ

У|-. .р

j

У вищезазначених рівняннях використані позначення:

X; (і = 1, 2, 3) — бактеріальна біомаса метілотрофа і двох видів гетірот-

рофів;

р, рпі — питома і максимальна питома швидкості росту і-го виду;

D — швидкість вимивання;

s;, Pj (j = 1 …4) — концентрації кисню, ССЬ, метанолу, етанолу і ацетату

в середовищі відповідно (верхній індекс (*) позначає концентрацію речовини в стаціонарному стані);

Кц (і = 1, 2) — коефіцієнт переносу маси для кисню і СО2 відповідно;

Yjj (і = 1, 2, 3; j = 1, 3, 4) — вихід бактерій виду і на j субстрату;

Ру (і = 1, 2, 3; j = 1, 3, 4) — коефіцієнт подоби виду і субстрату);

Рту (і = 1, 2, 3; j = 1, 2, 3, 4) — коефіцієнт чутливості бактерій виду і до метаболіту п;

у — — питома швидкість виділення внеклітинного метаболіту j бактерія­ми виду і.

У роботі Левича і Рокхема [51, 52] вивчено шість різних спо­собів лімітування: метилотрофні бактерії у всіх випадках ліміту­ються концентрацією розчиненого кисню, два види гетеротрофів лімітуються або обоє проміжними позаклітинними метаболітами, або обоє максимальною питомою швидкістю росту, або обоє кон­центрацією розчиненого кисню, або комбінацією двох різні факто­рів, що лімітують. Серед отриманих результатів необхідно відзна­чити можливість існування стійкої культури, що полягає із трьох бактеріальних видів, що конкурують за кисень.

Комментарии запрещены.