Бурение грунтовых зондов, установка энергетических колодцев

Розглянемо процеси, які описуються системою рівнянь:

diT^/dt = капкані! — кьішь т^О) = т10; (3.147)

dm2/dt = ка2іка4ті + kb2ikblmb т2(0) = т20; (3.148)

dm3/dt = ка31 ка4іті, + к1і3| кЬ|іП |, т3(0) = т30; (3.149)

dm4/dt = кМ|кміП| + ка4 ть т4(0) = т40; (3.150)

dcmT/dt = казікаДії! + kb51kb5]m] + 6(Tn-T)S, Т(0)=Т00; (3.151)

m = mi + m3 + m4 + m5; pH = (pH0 + 6i(m3/V))/(l + 62(m3V)); (3.152)

де
ka4 = ka4(T, pH, m4/V, m3/V) = ка1оріфа(Т)са(рН)ра(т4/У)за(т3/У) (3.154)
(3.155)
T < T < T min max
0,pH<pHmin (PH — PHmin) • (pH — pHmax )
ca(pH)	pHmin<pH<pH,
(pH — pHmm) • (pH — PHmax)- (pH — PHopt)2 ’ 0, pH>pHmas
Ma(m4/V) = (m4/V)/((m4/V) + Ks); (3.156) 3a(m3/V) = (Kin)/((m3/V)n + K»); (3.157) Кьі = Кы(Т iin3/V) = Kbiopt(|)b(T)Mb(m3/V); (3.158) Фьі(Т) = Т-Т0, (2.139) Визначення символів наведені в розділі 3.4.1. Тут величини m2, m3, m4, Т, pH представляють фазові координати, які визнача­ються рішенням системи (3.147)-(3.153). Вони утворяють деякий вектор фазових координат, що позначимо через F=( m2, m3, m4, T, pH). Крім того, у систему (3.147)-(3.153) входить ряд параметрів або коефіцієнтів. Параметри ка10рр, Тпшь Ттах, Т0рр, pHmjn, pHmax, рН0р^, K-s, Kj, kblopt, Ту, pHy, бь б2, V, каіь ка2і, к^і, ка51, кЬ21, кьз1 кЬ41, кЬ51 є відомими константами, обумовленими з апроксимації експеримен­тальних даних. Вони залежать від конкретних видів розглянутих процесів і утворяють вектор параметрів P=(kalopt, Tmin, Tmax, Topt, pHmin, pHmax, pHopt, Ks? K„ kbiopt, T0, V, кац, ка2Ь ka3b ka5b kb2b kb3, kb4i, kb5i pH0, 8i, б2,) і задаються видом розглянутого процесу. Якщо біомаса задана, процес визначений, то цей вектор-параметр також визначений. Вони визначаються видом розглянутих мікроорганіз­мів і процесами в них, вважається, що вони відомі.

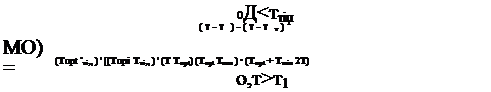Зовнішня температура Тп і, початкові умови т10, т2о, т30, т40, Т0о, залежно від постановки завдання, можуть бути і заданими ве­личинами, і збуренням, і керуванням (керуючими параметрами). Якщо деякі з них є заданими, то їх включимо як компонент у век­тор Р. Але в деяких з параметрів (Tn, т10, т20, т30, т40, Т0о), напри­клад, початкової температури, можуть бути відомі заздалегідь тіль­ки інтервали їхньої зміни, тобто припустимі області значень, а не самі значення. Вони можуть реалізовуватись по-різному залежно від стану зовнішнього середовища, і є величинами, що обурюють процес. Ці компоненти параметрів (Tn, т10, т20, т30, т40, Т0о) по­значимо через W, назвемо їхніми збурюваннями або параметрами, що обурюють процес. Загалом кажучи, збурювання перебувають у деякій обмеженій області, кожний компонент задовольняє деякій нерівності:

Тп0 < Тп < Тп1,

т10о <тіо <т10і, т20о <т20 <т20ь т3оо <т30 <тзоь (3.160) ПІ400 < т4о <т4оь Тооо 5Тоо<Тооі-

Цю припустиму область позначимо через W, тоді:

W = ( Tn, т10, т20, т30, т40, Т00) є W. (3.161)

Але, з іншого боку, у певних випадках всі або частина параме­трів (Тп, Шю, т20, т30, т40, Т0о) можуть перебувати в нашому розпо­рядженні, ми їх зможемо вибирати самі, по нашому бажанню в пе­вних межах із припустимої області. У число таких параметрів може включатися і обсяг V є [V0, VJ, де V0, Vi — гранично припустимі значення обсягу. При такій постановці завдання параметри Tn, т10, т2о, т30, т40, Т0о, V назвемо керуванням або керуючими параметра­ми. Керування позначимо через U=(Tn, m10, m20, m30, m40, T0o, V), компоненти якого також задовольняють нерівностям (3.160) і включенню V є [Vo, VJ. Область припустимих значень керування позначимо через U, тобто U є U. Ясно, що складові параметрів (Тп, Шю, m20, т30, т40, Т0о, V), які є керуванням, не може бути збурю­ванням і, навпаки, збурювання не є керуючими. Так що залежно від розглянутого завдання частина параметрів (Тп, pH, тиь т2и, тзи, т4о, Т0о, V) можуть бути заданими, обурюючими і керуюючими na­раметрами. Але одночасно бути тим і іншим не можуть. При рі­шенні конкретних завдань, залежно від постановки завдання, час­тина з них буде ставитися до заданих параметрів Р, інша частина до обурюючих — W, а якась до керуючих параметрів U. Помітимо, що деякі з керуючих параметрів можуть бути функціями часу, а інші постійними. Постійні керуючі параметри вибираються із припус­тимої області на початку процесу і далі не змінюються. Якщо оби­рані параметри є функцією часу, то називаються керуванням. Для скорочення викладу всі параметри, які перебувають у нашому роз­порядженні і вибираються, де це не приводить до ускладнень у ро­зумінні, назвемо керуванням.

Таким чином, система визначається параметрами чотирьох типів, які об означили F — фазові координати, Р — задані параметри, W — збурення, U — управління.

Далі слід розрізняти завдання двох видів:

— аналізу,

— синтезу.

Завдання аналізу складається в дослідженні впливу параметрів системи (наприклад, початкових умов, наружної температури и ін­ших параметрів) на поведінку системи, тобто фазових координат, визначаючих поведінку мікроорганізмів. При цьому задаються різ­номанітними наборами значень всіх параметрів, і решається систе­ма рівнянь (3.147)-(3.153) відносно фазових координат для кожного варіанту набору. Звичайно важко аналізувати вплив всіх парметрів одночасно, тому досліджується вплив окремих найбільш вагомих параметрів. По результатам цих досліджень визначається ступінь впливу окремих параметрів на процес і вибирається найбільш при­йнятний варіант.

Задача аналізу зводиться до рішення системи (3.147)-(3.153) при заданих значеннях параметрів. При аналізі значення параметрів являються заданими, але варіюються.

В задачі синтезу задаються визначені вимоги до поведінки си­стеми — обмеження на фазові координати, допустимий клас збу­рень, і будується множина управлінь, які задовольняють цим вимо­гам. Наприклад, обмеження на фазові координати задаються у ви­гляді нерівності:

тш < mi < т1Ь т02 < т2 < т12, т03 < т3 <т13, т04 < т4 <т14, (3.162) Т0Т < Т < Т1Х, рН0р < pH < рН1р.

Ці нерівності визначають допустиму межу фазових координат, яку об означимо через F, тобто F є F. Не всі нерівності (3.162) мо­жуть бути двосторонніми. Якщо, наприклад, нижня межа неважли­ва для якогось параметра, то покладається, що він рівняється -оо. Якщо верхня межа неважлива для якогось параметра, то поклада­ється, що він рівняється +00. Так що нерівності, які обмежують фа­зові координати, можуть бути двосторонніми, однобічними і зовсім не мати обмежень. При постановці завдання синтезу можуть бути задані іншого виду обмеження на фазові координати, наприклад, програма поводження деяких фазових координат. Тут розглянемо обмеження типу нерівності (3.162).

У завданні синтезу потрібно визначити керування U системою із припустимої області U так, щоб при всіх припустимих збурюван­нях W є W вектор фазових координат F задовольняв нерівностям (3.162), тобто F є F.

У такий спосіб основні параметри, що характеризують функ­ціонування системи F=(mb m2, m3, m4, Т, pH) повинні перебувати в певних межах, що задають технічними умовами (3.162). Якщо зна­чення хоча б одного з них виходить за зазначені межі, то функціо­нування системи є незадовільним. Наприклад, якщо вихід газу ш2 стає занадто низьким, порушується нерівність ш02< ш2, а вихід тве­рдих ВІДХОДІВ Ш3 — ВИСОКИМ, порушується нерівність Ш3<ГПі3, то це означає, що функціонування системи стає не задовільним з погляду постановки завдання. Якщо поводження окремих параметрів сис­теми не має значення, то відповідні обмеження варто просто ви­ключити. У противному випадку вибором керування необхідно до­могтися, щоб параметри системи були в заданих межах, якщо це можливо. Проектувальник або особа, що приймає рішення не може впливати на фазові координати безпосередньо, а тільки через конс­труктивні параметри або керування, які він вибирає за своїм розсу­дом.

В даній роботі параметрами, якими проектувальник безпосе­редньо задається, і тим самим впливає на робочий процес, є деякі з параметрів U=(Tn, pH, m10, m20, m30, m40, T00, V). У такому випадку вони і є конструктивні параметри або керування. Варто помітити, що на процесе функціонування системи впливають також парамет­ри (каїорь Тщш, Ттах, ТорЬ рНщіл, pHmax, pHopt, Ks K„ kblopt, Tq, V, ka] [, ка2ь ka3|, ka51, kb2b kb31 kb41, kb5b pH0, бь б2,). Якщо деякі з них можна вибирати в певних межах, то їх також варто розглядати і вибирати як конструктивні параметри.

Система працює в різних зовнішніх умовах. До них можуть бути віднесені зовнішні, початкові умови, наприклад, (Тп, пію, т20, т3о, т40, Т0о). Від них також залежать процеси, що протікають у си­стемі. Якщо не передбачена можливість керування ними, то на ці параметри, що обурюють, ми вплинути не можемо. Але в той же час потрібно, щоб система нормально функціонувала, коли ці пара­метри зовнішніх умов перебувають у певних припустимих межах.

Таким чином, задача синтезу зводиться до рішення системи рівностей і нерівностей, причому диференціальних і алгебраїчних, при деяких невизначеностях. Найчастіше, якщо система нерівнос­тей має рішення, то є не єдине, а ціла множина рішень. Всю мно­жину рішень назвемо повним рішенням задачі синтезу. У виді складності рішення системи нерівностей часто доводиться будува­ти не всі, а тільки одне або кілька рішень. Такі рішення назвемо по­вним рішенням задачі синтезу.

Задача синтезу не завжди має рішення. Якщо обмеження (3.161), (3.162) занадто тверді, то рішення системи нерівностей мо­же не існувати. Таким чином, необхідно визначити чи має дана за­дача синтезу рішення, якщо має, то, треба його знайти. Задача син­тезу параметрів системи або керування складніше, ніж задача ана­лізу. Тепер розглянемо необхідну й достатню умову можливості розв’язання задачі синтезу.

Така постановка задачі близька практичної стійкості в механі­чних системах, де розглядається задача знаходження траєкторії ру­ху в заданих областях початкових і наступних станах системи на заданому проміжку часу. Для некерованих систем ця задача розгля­нута в роботах: [78, 79], а стосовно до задач синтезу практично стійких керованих систем у роботах [80, 81] і інших.

3.4.11 Необхідна й достатня умова можливості розв’язання і

загальний алгоритм рішення задачі синтезу параметрів системи

Введемо позначення:

У1 = тої — Шь У2 = 1ЇІ! — т„; у3 = т02 — пц; у4 = т2 — т12;

у5=т0з-ті; у6 = т3-т13; у7=то4-т1; у8=т4-т14;

у9=Т0Т-Т; у10 = Т — Tlt; уц = рН0р-рН;

Уі2 = рН-рН1р, (3.163)

і двосторонні нерівності (2.142) запишемо у вигляді однобіч­них:

Уі<0, jeJ, J= {1,2,…12}. (3.164)

Змінні yj, j є J визначаються формулами (3.163), фазові коор­динати mb т2, т3, т4, Т, pH, що входять у формули (3.163) — рі­шенням системи рівнянь (3.147)-(3.153). Таким чином, задача син­тезу зводиться до побудови керування (або множини керувань), що задовольняє умові U є U і виконання, що забезпечує, нерівностей yj < 0 при всіх збуреннях W є W, де j є J, yj визначаються формулами (3.163) і рівняннями (3.147)-(3.153). Змінні yj залежать від парамет­рів (W, U). Ці залежності запишемо у вигляді yj=yj(W, U).

Для рішення задачі синтезу використаємо ідею робіт [7, 8,10, 13, 14, 16-19, ЗО, 32, 33, 39, 42, 65-70, 75, 77]. У цих роботах задача синтезу називається основною задачею керування (ОЗУ), якщо бу­дується керування системою або основною задачею проектування (ОЗП), якщо будуються постійні параметри системи. Тут розгляда­ються обидві задачі.

Необхідна й достатня умова існування рішення цієї задачі да­ється наступною теоремою.

Теорема 1. Для того щоб система рівностей і нерівностей (3.147)-(3.164) мала рішення, необхідно й досить, щоб виконувала­ся умова:

у0 = min max max ij (W, U) < 0. (3.165)

Доказ. Необхідність. Це твердження майже очевидно. Допус­тимо, воно порушується. То це означає, що найдеться хоча б один параметр збурювання W і номер j є J параметрів yj, для яких не іс­нує припустимого значення керування U є U, такого, щоб викону­валася нерівність yj(w, u) <0. Звідки треба необхідність виконання умови (3.165).

Достатність. Якщо нерівність (3.165) виконується, то це озна­чає, що для всіх припустимих збурювань W і параметрів yj існує, хоча б одне припустиме значення керування U є U, при якому всі нерівності виконуються й рівняння мають рішення. Це те керуван­ня, що мінімізує max max yj(W, U). Крім того, можуть бути і інші керування.

Це досить загальна необхідна й достатня умова існування рі­шення задачі синтезу. Воно не визначає рішення системи рівностей і нерівностей, а представляє необхідну й достатню умову існування її рішення і дає напрям, в якому слід шукати рішення в методі по­слідовних наближень. Пошук рішення повинен іти у напрямі вели­чини мінімакса у0. Якщо знайдеться управління U є U, при якому виконується нерівність:

у =max max y](W, U) <0, (3.166)

то це U є приватним рішенням задачі синтезу або ОЗУ. На основі цієї ідеї розроблений ряд приватних методів чисельної побудови рішення ОЗУ. їх можна знайти в роботах [7, 10, 13, 14, 17, 18, 32, 39, 66-70]. Тут приведемо загальний алгоритм побудови рішення ОЗУ методом послідовних наближень, зокрема випадкового пошу­ку [5, 6, 18, 44,71-73]:

1 крок. Задаємося початковим наближенням рішення U(0). При цьому, взагалі кажучи, не всі нерівності yj(W, U) <0, WeW, j=l, 2…, J=12 можуть задовольнитися, так як U=U(0), взагалі кажучи, не є рішенням системи нерівностей (3.164). Тепер покладемо (0)=(і).

2 крок. Перевіряємо виконання нерівностей y/W, U(l))<0, j=l,

2.. ., J. Якщо виконуються всі нерівності, то одне рішення знайдене, отже, рішення існує і на цьому процес рішення можна припинити. Інакше, якщо хоч би одна нерівність y/W, U(l)) <0, WeW, j=l, 2…, J не задовольняється, переходиться до наступного пункту.

3 крок. Перевіряємо, чи не досягнутий minmax{yj(W, U}. Якщо досягнутий мінімакс і minmax{yj(W, U)}>0, то система нерів­ностей (3.166) не має рішення. Обчислення на цьому припиняють­ся. Інакше обчислюємо значення у/ =yj(W, U(l)) для всіх WeW, j=l,

4 крок. Знаходимо шаху/ =max{yj(W, U(l)), W є W, j=l, 2…, J}. Хай це досягається при j=j і W=W. Тоді у,*’ =max{yj(W, UUj), j=l,

2.. ., J). Якщо максимум досягається одночасно для декількох зна­чень j або W, то вибираємо одне з них, і продовжуємо рішення.

5 крок. Розглянемо функцію максимуму у,* =max{yj(W, U)},

sj: § f ^ u m

тобто при W=W, j=j. Ця функція має найбільше значення серед

всіх у,* =yj(W*, U) у точці U=U(l).

• • •

6 крок. Далі здійснюється спуск по функції Уі*=Уі {W, U). Це

може здійснюватися будь-якими відомими методами, наприклад, методом випадкового пошуку, покоордінатного спуску, градієнтно­го спуску і т. д.

6* крок. Якщо спуск здійснюється по градієнту функції yj*=yj(W, U), то спуск робиться на деякий малий крок AU, як це прийнято в методі градієнтного спуску. Набутого значення параме­тра U(l+1), що управляє приймаємо за наступне наближення: у(і+!)=у(і) +ди(0 де дуб) _ поправка до попереднього наближення, яка згідно методу градієнтного спуску записується AU(l) = — edy/dU, а е представляє крок градієнтного спуску — мале позитивне число. Похідна dy/dU обчислюється в точці U#U(l). Надалі замінюючи і+1 на і, переходимо до кроку 2.

Зауваження І. При пошуку рішення послідовними наближен­нями в кожному кроці обчислюється max max yj (W, U), а потім спуск здійснює по функції yj(W, U), яка приймала максимальне значення. В принципі в деякому кроці максимальна функція і, отже, функція уздовж якої здійснюється спуск, може мінятися. Индекс j=j* може мінятися при переході від даного кроку до наступного, тобто спуск може здійснюватися не завжди по гладкій функції. Це викликає деякі складнощі при пошуку рішення із-за «овражної си­туації». При здійсненні пошуку це треба мати на увазі.

Зауваження 2. Тут необов’язково шукати екстремальну точку min max max{yj(W, U)}, достатньо пошук продовжувати до задово­лення нерівностей (3.166). Метою процедури пошуку є побудова хоч би одного рішення цих нерівностей.

Зауваження 3. При чисельній реалізації безперервні парамет­ри зазвичай приблизно замінюються дискретними. Дискретизація проводитися за часом і по величині параметрів.

Комментарии запрещены.