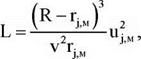Бурение грунтовых зондов, установка энергетических колодцев

Сучасне енергоспоживання зводиться, в основному, до викорис­тання природних (первинних) паливно-енергетичних ресурсів, таких, як викопне паливо і продукти його переробки (моторне паливо, ма­зут), а також ядерне паливо. Це зв’язано, головним чином, з відносно нескладним процесом отримання цих видів палива при їх високих енергетичних потенціалах.

Найважливішим чинником, що впливає на ситуацію в енергетиці і економіці як в світі в цілому, так і для України зокрема, є істотне збільшення цін на енергоносії, зокрема, на природний газ. У зв’язку з чим, ще актуальнішим стає завдання пошуку альтернативних джерел енергії.

Використання методів біологічної конверсії органічних відходів з метою отримання газоподібного або рідкого палива в даний час є вельми перспективним. Це дозволяє вирішити не тільки енергетичну проблему, але також економічну і екологічну, тому привертає увагу фахівців-екологів, енергетиків, економістів, біотехнолотів. Вона ве­
льми істотна для сільського господарства, де є велика кількість орга­нічних відходів. Переробка даних відходів здійснюється в біогазовій установці, це детально вивчено авторами [1, 3, 276]

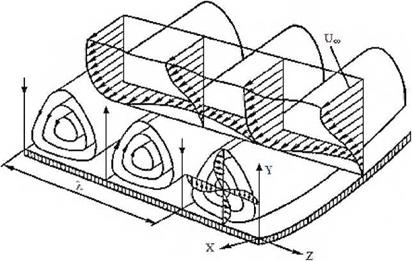
Елементом біогазової установки є шнек — пристрій, що закручує субстрат для подачі в реактор. У шнекових стрічкових завихрителях вихід субстрата відбувається відповідно до закону обертання твердого тіла. З технологічних міркувань при геометричному вугіллі закручу­вання ср<=450 зазвичай використовують стрічкові завихрителі, а при ср>450 — шнек (рис. 6.11).

Найбільшого поширення набули перемішування в рідких сере­довищах за допомогою механічних мішалок [1, 2]. Авторами даної даних робіт вирішувались питання перемішування субстрату за допо­могою механічних мішалок в реакторі біогазової установки, детально вивчивши енергетичні питання, пов’язані з роботою шнекового при­строю в біогазовій установці, і отримати залежності в примежовому шарі від конструктивних параметрів шнека.

У загальному випадку геометричний кут закручування на зовні­шньому діаметрі dm=2R багатозаходного шнека визначається виразом

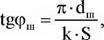(6.16)

де S — крок шнека, k — число витків.

Величина кроку шнека не залежить від відстані між віссю шнека і даним циліндровим перетином, тому при зменшенні радіусу геомет­ричний кут зменшується.

Важливою геометричною характеристикою шнека є еквівалент­ний діаметр каналу, який обчислюється за наступними формулами:

для шнека з прямою канавкою

2	(s — sin фсср — 8^	)'(din — d0)
4	S-sincpcep -8)	+ (dm-d0)

(6.18)

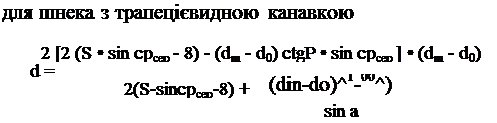• для шнека з навивкою

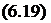
d _8S-sincpcep-(dI11-d0)-7r(dI11-d0)2 2 [4 S • sincpcep + n (dm — d0)]

• для шнека з напівкруглою канавкою

= 7r(S-sincpcep-8) = 7r(din-d0)

О О 5

2 + 71 2 + 71

де Фсер — геометричний кут закручування на середньому діаметрі;

8 — товщина ребра шнека при вершині в площині поперечного перетину гвинтової канавки;

Р — кут, що характеризує форму трапецієвидної канавки;

dm — діаметр шнека;

do — діаметр серцевини шнека.

Важливою геометричною характеристикою стрічкового завих — рителя є його крок S, який рівний осьовому розміру завихрителя при повороті закрученої стрічки на 180°. Кут закручування потоку біля поверхні труби однозначно пов’язаний з відносним кроком (відно­шення кроку S до діаметру труби d)

tg<P«p=f^. (621)

Для каналу, утвореного стінкою труби і стрічкою товщини, що округляє б, еквівалентний діаметр визначається по формулі

d(7r-d-48)

3 ~~ 7r-d + 2(d-8)

Слід зазначити, що при обтіканні необмеженим потоком криво­лінійної стінки виникає нормальна до поверхні відцентрова сила, яка збільшується у міру видалення від поверхні і стає найбільшою на зов­нішній межі прикордонного шару. При обтіканні увігнутої поверхні напряму масової сили і градієнта скалярного поля масових сил grad|F| будуть протилежними. В цьому випадку в прикордонному шарі мо­жуть з’явитися мікровихори з осями, паралельними поверхні, і з на­прямами обертання, що чергуються, тобто вихори Тейлора-Гертлера (рис. 6.12).

X — довжина відривного примежового шару; Ц» — швидкість течії за ме­жами примежового шару. Рисунок 6.12 — Вихори Тейлора-Гертлера в примежовому шарі

Для характеристики інтенсивності закручування потоку за завіх — рітелем користуються поряд параметрів. Авторами роботи [277] за­пропонований параметр:

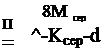де Мдер — усереднений момент кількості руху потоку; Keep — усереднена кількість руху;

d — діаметр каналу.

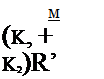На думку автора [277], інтенсивність закручування потоку зави- хрителем доцільно характеризувати вхідним параметром

де індекси 1 і 2 відповідають осьовій і закрученій течії;

R — радіус каналу.

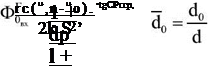Для шнекового завихрителя з прямокутною канавкою і постій­ним по довжині кроком

d — діаметр каналу; k — число витків;

S — крок шнека.

Дійсне значення інтенсивності закручування потоку відрізня­ється від приведених формул. Це обумовлено нерівномірністю полів швидкостей в каналах завихрителей, гідравлічними втратами на тертя і т. д. Для шнекового завихрителя з прямокутною канавкою рівняння, що зв’язує дійсний і розрахунковий параметри повного закручування потоку має вигляд

Фовх = 1Д8сС. (6.27)

Для отримання узагальнених залежностей використовують ме­тоди теорії подібності. При вивченні ізотермічних нестискуваних по­токів безрозмірне число

(6.28)

де 1 — характерний розмір;

Aj = j’max-jmin — різниця між максимальним і мінімальним прискоренням;

ц — коефіцієнт кінематичної в’язкості рідини.

При вивченні гідродинамічного опору в ізотермічних потоках, що знаходяться під впливом масових сил, результати дослідів можна узагальнити рівнянням

|,c,=f(Re, L), (6.29)

де £, — коефіцієнт опору тертя для внутрішнього завдання;

Cf — коефіцієнт тертя для зовнішнього завдання;

Re — число Рейнольдса.

У закрученому потоці нестискуваної рідини поле масових сил однозначно визначається зміною прискорення

де u — окружна швидкість, г — радіус.

Зміна прискорення j, у свою чергу, визначається полем окруж­них швидкостей. Число L для закрученого потоку

де rj M і Uj M — радіус, відповідний jMaKC, і окружна швидкість на цьому радіу­сі.

Дослідження показують, що закручування потоку зменшує еріті — чеськоє число Re, відповідне втраті стійкості ламінарного потоку в трубі. При Re<1800 втрата стійкості з’являється в наслідку виникнен­ня неперіодичних синусоїдальних коливань цівок. При Re>2500 не­стійкість з’являється у вигляді ряду вихорів, що виникають з певною частотою. Ці вихори швидко збільшуються і приводять до утворення турбулентності.

Важливе питання відноситься до гідравлічного опору шнека.

При перебігу потоку через шнек виникають втрати тиску на вхо­ді і виході з нього, а також усередині самого шнека.

Вхідні втрати тиску виникають унаслідок зміни напряму руху потоку. Ця складова може бути помітно зменшена застосуванням шнекових завіхрітелей змінного кроку з нульовим кутом закручуван­ня на вході [278].

Вихідні втрати викликані раптовим розширенням площі попе­речного перетину, зміною напряму потоку і перемішуванням дискре­тних струменів, витікаючих з шнека.

Втрати тиску усередині шнека обумовлені нерівномірністю поля швидкості унаслідок виникнення вторинних течій, а також трьохмір — ним характером перебігу в каналі шнека.

Сумарно всі види втрат визначаються у вигляді коефіцієнта опор

або коефіцієнта гідравлічного опору

де Др*у — перепад повного тиску на стінці до і після завихрителя; le, de — еквівалентна довжина гвинтової лінії на середньому радіусі і екві­валентний діаметр гвинтового каналу шнека, відповідно;

Ucep — середня швидкість потоку в трубі із завихрителем. Експериментально досліджений гідравлічний опір дво і чотири-

заходних шнекових завихрителей з прямокутною канавкою при пере­бігу повітря в умовах повного і часткового закручування. В результаті узагальнення досвідчених даних отримані рівняння

[1 + 9,380^ Дго [і + 6,63Ф^4 ’

Еквівалентний діаметр в приведених вище формулах визначаєть­ся по формулі

2(S sin cpcp — 8)(<ДШ — dQ)
2(S sin cpcp — 8) + (dm — dc)

Рівняння отримані в наступному діапазоні змін визначальних параметрів:

Фсе = 30…60°; г=0,4…0,6;

Ф*вх =0,09…1,69; Ree=-^ = (1,2…6,2)-10

У даному діапазоні чисел Рейнольдса має місце ламінарний мі — кровихровий режим течії, тобто під впливом відцентрових масових сил перехід від ламінарного течії до турбулентного в значній мірі за­тягнутий. Для коефіцієнта гідравлічного опору завихрителів запропо­нована наступна формула

, — іО. З
		(6.35)
• о11

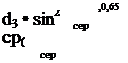де С=4,9 — для шнекових завихрителів, навитих дротом;

С=5,5 — для нарізних шнеків; deep — середній діаметр;

Ф*вх

0 = —2^- — співвідношення параметрів закручування шнека в умовах част — фи

*ВХ

кового і повного закручування.

Осьовий розмір завихрителя розраховується за виразом:

з. і

h = 0,84 + 0,54

Реальні в’язкі закручені потоки найчастіше описуються двомі — рними рівняннями для трьох компонент швидкості. Двомірність є наслідком припущень про азимутну симетрію локальних парамет — рів(<3/<3ф=0).. При цьому властивості течії можуть описуватися пара­болічними рівняннями (типу прикордонного шару) або частіше еліп­тичними (тертя із зворотним струмами) і, залежно від цього, схеми

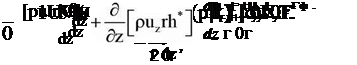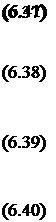рішення виявляються різними. Слабо закручені потоки і струмені без осьової реціркуляційної зони відносяться до перебігу першої катего­рії. Рівняння, що описують їх, мають наступний вигляд [279, 280].

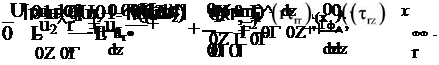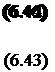Сильно закручені течії, в яких закручування достатньо велике для утворення центральної тороїдальної рециркуляционной зони, від­носяться до другого, тобто еліптичному типу. Еліптичні рівняння для закрученого потоку мають наступний вигляд [5, 6, 7].

—[pu rCt ] +—[pu rCt ] = — [rm ] + — [rm ] + W;,

0rL r tJ 0zL z tJ 0rL rtJ 0zL ztJ

де Сі — концентрація кожного компоненту; mrt, mzt — складові масового потоку речовини;

Wi — швидкість утворення (зникнення) масового потоку речовини;

Ні — питома теплота утворення (зникнення) масового потоку речовини; h* — ентальпія гальмування (повна ентальпія);

ur, Uj, uz — швидкості, що становлять, в циліндровій системі координат; qr, qz — складові питомої щільності теплового потоку.

Напруга, яка входить в рівняння, визначає по наступних співвід­ношеннях [281].

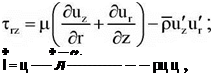
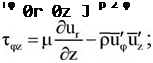(6.48)

(6.49)

(6.50)

СПГ _/ , 2

тгг=2ц—^-p(uz) ,

0Г

(6.52)

(6.53)

CZ Щільність теплового потоку, що становить

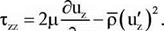
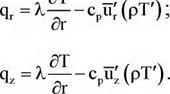(6.54)

(6.55)

Складові масового потоку

(6.57)

Для ламінарного потоку всі складові пульсацій рівні нулю. На значення коефіцієнта подачі шнека кр в умовах анізотропного тертя великий вплив робить співвідношення fx/fy (коефіцієнт тертя матеріа­лу об циліндр уздовж осі шнека до коефіцієнта тертя у напрямі обер­тання шнека), яке, у свою чергу, залежить від відношення коефіцієн­тів зовнішнього тертя матеріалу об метал циліндра f4 і внутрішнього тертя матеріалу fM, від розмірів, форми і кількості тих, що направля­ють.

Оптимальні геометричні параметри робочих органів шнекового вузла, при яких забезпечується максимальна продуктивність установ­ки заданими розмірами і швидкістю обертання шнекового валу при транспортуванні різних матеріалів, описується співвідношенням

[279]:

0Факт=£(у, а,ь, і);

де у — кут нарізки гвинтової лінії шнека; а — відстань між тими, що направляють; b — висота тих, що направляють;

1 — ширина тих, що направляють.

о

Продуктивність шнека, м /хвил. [279]:

(6.59)

де dm — діаметр шнека, м; dc — діаметр ступеня шнека, м; п — частота обертання, хвил-1.

Елементом біогазової установки є шнек, що є пристроєм, що закручує, для подачі субстрату в реактор. У шнекових і стрічкових завихрителях вихід субстрату відбувається у відповідності із зако­ном обертання твердого тіла. Найбільшого поширення набули пе­ремішування в рідких середовищах за допомогою механічних мі­шалок [282]. Виходячи з цього, доцільним є вивчення процесу пе­ремішування субстрату за допомогою механічних мішалок в реак­торі біогазової установки, отримання математичних співвідношень технологічних параметрів перемішування від параметрів установки та гідродинаміки перемішування гетерогенних середовищ і встано­вити залежність названих характеристик від числа Фруде в апара­тах з відображеними перегородками і в гладкостенних апаратах.

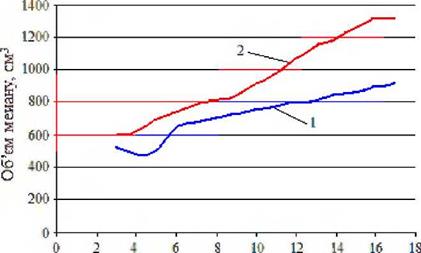
Перемішування механічними мішалками. Процеси перемі­шування в рідких середовищах за допомогою механічних мішалок широко поширені в багатьох галузях техніки. Перемішування з ви­користанням механічних мішалок гомогенізує гетерогенні системи і інтенсифікує технологію отримання двофазних середовищ [282]. Результати досліджень по вивченню впливу процесу перемішуван­ня на кількість біогазу, що виділяється, приведені на рисунку 6.13 [283, 284]. Можна відмітити, що вихід метану збільшується майже в 1,5 разу.

Час зброджування, доба 1 — стаціонарний режим; 2 — при перемішуванні Рисунок 6.13 — Динаміка виходу метану при анаеробному зброджуванні гною великої рогатої худоби

Тангенціальний потік від мішалки є осесимметрічним і опису­ється системою рівнянь

д д —(rvr) + r—(vz) = 0, dr dz	(6.60)
dve for vo 1 fof)7 v —— + v —L + — =——————— —, dr dz r p dz	(6.61)
v | v ^0 , Vr‘V0 _ 1 foez dr dz r p dz	(6.62)

де vr, ve, vz — компоненти середніх швидкостей в циліндрових коорди­натах; T()z — компоненти тензора зрушення; г — щільність рідини.

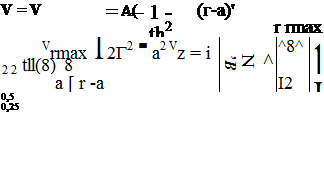Припустимо, що тангенціальний потік одновимірний. В цьому випадку для профілю швидкості в напрямах г і z слідують співвідношення

(6.66)

А — параметр об’ємного потоку; а — параметр ширини тангенціального потоку; th — гіперболічний тангенс.

Система рівнянь містить три похідні константи: А, а і а, які визначаються з граничних умов.

Для результуючого вектора швидкості q і компонентів vr і vz є співвідношення

Для області з потенційним потоком маємо вираз функції стру­

1|} = r2z.

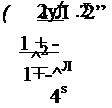Циркуляційний потік у напрямі осі в центрі апарату в турбу­лентній області течії може бути представлений рівняннями

де 8о — коефіцієнт вихрової в’язкості;

у — параметр, що характеризує ширину циркуляційного потоку;

Z- координата, відповідна циркуляційній області течії;

— безрозмірна координата, визначувана із співвідношення

• (6.71)

Z + Zj

Результати розрахунку по приведених вище рівняннях дозво­ляють отримати тільки якісну картинку течії, але не кількісні дані.

У гладко стінних апаратах перемішування супроводжується утворенням центральної воронки. Глибина і форма воронки харак­теризують ефективність технологічного перемішування. Цьому пи­танню присвячений ряд досліджень. Результати експериментальних даних, як правило, представлені у вигляді критерійних залежнос­тей.

Для радіально-лопатевих мішалок запропонована розрахунко­ва формула, по якій визначають глибину воронки [284]:

г„ =-|—= С2Г-г1м.(1,59-0,75-Г;-45), (6.72)

им

де її — глибина центральної воронки; dM — діаметр мішалки;

Для дослідження процесів перемішування рекомендується ко­ристуватися математичними моделями, заснованими на принципах гідродинаміки рідини, широко описаних авторами [285-287].

Тому в першому наближенні рекомендується виходити з мо­делі ідеального змішування, яка є моделлю макрозмішування. При цьому не враховуються локальні, дрібніші явища. Така модель, зок­рема, особливо доцільна за відсутності механічного перемішуван­ня, коли енергія вхідного потоку витрачається на утворення конве- ктивних струмів і турбулентних вихорів, які і викликають перемі­шування рідини в апараті. У цих випадках для опису фізичних явищ, що протікають в апараті, слід звернутися до рівнянь Навье — Стокса і можна не приймати до уваги прискорення поля зовнішніх масових сил, а також перепад тиску в об’ємі рідини, оскільки вони нехтує малі в порівнянні з інерційними силами і силами тертя.

В результаті рівняння руху має вигляд [287]:

де D — оператор диференціювання;

Wi — швидкість; т — час;

v — кінематичний коефіцієнт в’язкості;

V2 — оператор Лапласа

vy2 _ & д2 д2

V ——т-л — ч —

дх2 ду dz2

Рівняння енергії записується так

— = aV2t, (6.75)

dx

де t — температура; а — температуропровідність.

Для процесу перемішування має значення енергія, що витра­чається на подолання сил в’язкого тертя, яка визначається з виразу

E.=pJ<DvdVp,

Vr

де ц — динамічний коефіцієнт в’язкості; Vp — об’єм реактора;

Ф¥ — функція дисипації Релея

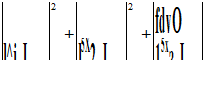(6.77)

+ &w2 ‘ +—- z + ґ &W, +—1 z + "dw2 dw^ + —1 [dx2 dx, J l5x3 dx, J 15хз dx 2 )

де Wi, W2, W3 — проекція вектора швидкості на осі х, у, z.

Рівняння руху в безрозмірній формі запишеться таким чином

—V2w15(6.78)

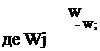Re

wcp — середня швидкість рідини в апараті; X — характерний лінійний розмір;

D — діаметр реактора;

Re — критерій Рейнольдса.

Рівняння після ряду простих перетворень приводиться до без­розмірного вигляду

Дослідження показали, що режим ідеальної рідини застосов­ний при Re>13,5.

Якщо перемішування не підкоряється законам руху рідини, необхідно звернутися до інших моделей для їх опису. У процесах неідеального змішування спостерігаються дифузійні явища. В цьо­му випадку математична модель в безрозмірному вигляді є зв’язок між числами Пекле і Рейнольдса

де ReKp=13,5,

Re

Re =89,31-In—^ m Re

Комментарии запрещены.