Бурение грунтовых зондов, установка энергетических колодцев

Чтобы расчистить завалы на пути квантовой теории гравитации (КТГ) необходимо вернуть физике светоносную среду, как реальное проявление сверхсильного

электромагнитного взаимодействия (СЭВ). Отказ от абсолютного пространства привел к необоснованному отказу от понятия светоносной среды, наделив электромагнитную волну свойствами самостоятельного поля, не требующего носителя. Возврат к идее единого поля Эйнштейна, которое является одновременным носителем электромагнетизма и гравитации, требует доказательства, что электромагнитная волна не может образоваться без квантованного пространства-времени, как единого поля. Если кто-то станет писать книгу научных заблуждений, то наиболее ярким примером такого заблуждения станет отказ от светоносной среды и придание электромагнитной волне свойств самостоятельного электромагнитного поля, не требующего носителя. Можно представить себе морские волны без воды? Точно также нельзя представить электромагнитные волны без светоносной среды.

Несмотря на то, что в работе [1] подробно рассмотрены причины электромагнитных взаимодействий как свойства квантованного пространства-времени, необходимо, хотя бы кратко показать еще раз, что квантованное пространство-время, как светоносная среда, является реальностью. Меня, не только как теоретика, но и экспериментатора, удивляет наивность теоретиков, совершенно не владеющих методологией проведения экспериментальных работ. В 20 веке теоретики исключили светоносную среду, которая существовала в физике более 200 лет до этого, благодаря гигантам физической мысли, таких как Декарт, Гюйгенс, Фарадей, Максвелл, Герц и многих других. Причем такое исключение делалось на основании опытов Майкельсона и Морли, которые, как показывает анализ, доказывают фундаментальность принципа сферической инвариантности в условиях квантованного пространства-времени, но не исключают специфичной светоносной среды. Чтобы исключить светоносную среду как таковую, необходимо поставить методически корректный эксперимент. Для этого необходимо взять трубу и удалить из нее физический вакуум, то есть светоносную квантованную среду, и посмотреть проходит свет в такой трубе, или не проходит. Если свет не проходит, то причиной его распространения служила светоносная квантованная среда, которую мы удалили из трубы. Но такого прямого эксперимента никто не ставил. Опыт Майкельсона и Морли по обнаружению эфирного ветра, как недоказанного свойства светоносной среды, нельзя считать корректным по отношению к светоносной среде.

Методически ситуация специально доведена до абсурда, поскольку удалить светоносную квантованную среду из трубы в земных условиях не представляется возможным. Но поскольку такого эксперимента никто не проводил, то удалить светоносную среду из физики также никто не имел права. Именно исключение светоносной среды довело ситуацию в физике до абсурда, когда логику физического эксперимента в теории заменили абстрактными математическими моделями, опираясь на методически некорректно поставленные опыты. Трудно представить себе, как можно манипулировать сложнейшими формулами, пытаясь найти решение вопроса, не зная его физической модели. Модель квантованной светоносной среды, которую представляет квантованное пространство-время, оказалась настолько удачной, что позволила объяснить не только структуру всех основных элементарных частиц, включая фотоны — переносчики света, но и разобраться со всем спектром проблем электромагнитных волн в уравнениях Максвелла. Напомню, что свои гениальные уравнения Максвелл записал без аналитического вывода, основываясь на концепции светоносной среды, полагая, что распространение любой волны без среды невозможно [21].

Парадоксально, но именно роторные модели электромагнитных волн в уравнениях Максвелла без всякого обоснования позволили исключить светоносную среду, опираясь на отрицательные результаты опытов Майкельсона и Морли в попытках обнаружить эфирный ветер, который не имеют никакого отношения к светоносной среде. При этом додумались считать, что электромагнитная волна — это особое вихревое состояние электромагнитного поля, когда вихрь магнитного поля порождает вихрь электрического, и наоборот, формируя электромагнитную волну, как самостоятельное поле. Это чисто метафизический подход, лишенный материального основания. Как можно создать вихрь в абсолютной пустоте? Чтобы идти вперед, необходимо отказаться от различных вихревых концепций в электромагнетизме, напоминающих эфирный ветер. В квантованном пространстве-времени есть электромагнитные роторы и круговые поля, но не вихри. Это экспериментальный факт.

Исследуя роторное состояние квантованного пространства-времени в

электромагнитной волне, мною не обнаружено в них вихрей. Под вихрем имеется в виду вращение среды вокруг некого центра. Квантованное пространство-время представляет собой сверхтвердую и сверхупругую среду, закрутить которую в вихрь, по типу газоподобного эфира, просто невозможно. Свойства пространства-времени не позволяют этого сделать. Можно изменять топологию квантованного пространства-времени в соответствии с (1) когда в пространстве-времени проявляется электромагнетизм или гравитация. Чтобы создать электрический или магнитный ротор, необходимо топологию квантованного пространства-времени изменить так, чтобы замкнуть по окружности электрические или магнитные оси квантонов в результате ориентационной поляризации [1]. Но ориентационная поляризация квантонов в виде окружности даже близко не напоминает вихрь, поскольку квантоны не закручиваются в вихревой поток, как частицы воды или газа.

Но проблема роторов и круговых полей в электромагнетизме не самая главная, поскольку на передний план выступает природа магнетизма и электричества, и механизм преобразования электричества в магнетизм, и наоборот. Пока физика связывает природу магнетизма с динамическим электричеством. Это метафизический подход, поскольку магнетизм проявляется как волшебство, неизвестно откуда. Но магнетизм есть реальная материальная среда, которая требует своего носителя в виде магнитных зарядов (монополей Дирака). Современная физика рассматривает магнитные монополи как гипотетические частицы, до сих пор не обнаруженные экспериментально. Новые открытия показывают, что магнитные монополи связаны внутри квантона в магнитные диполи, и в свободном состоянии не существуют. Напрямую обнаружить свободные магнитные заряды не представляется возможным, а вот косвенное их проявление экспериментально наблюдается во всех электромагнитных процессах, когда из электричества рождается магнетизм, и наоборот.

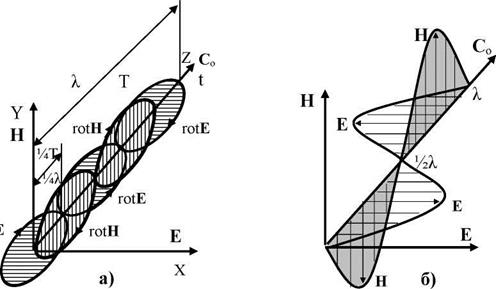
Если анализировать общепризнанные труды по теории электромагнетизма, то практически обнаружим одно и тоже повторение формального подхода к уравнениям Максвелла в вакууме при объяснении вихревой природы электромагнитной волны [22-28]: «Сегодня мы предпочитаем считать образование вихрей магнитного поля при изменении поля электрического, точно также как образование вихрей электрического поля при изменении магнитного поля, основным свойством электромагнитного поля» [28]. На рис. 1 а представлен ложный вихревой механизм распространения электромагнитной
волны, когда вихрь магнитного поля порождает вихрь электрического, и, наоборот, в направлении распространения электромагнитной волны. Вихри записаны через роторы Е и Н, лежащие в ортогональных плоскостях. При этом, чтобы ротор Н мог родить ротор Е, они должны быть сдвинуты по фазе во времени на четверть периода УТ Другого объяснения классическая электродинамика не знает. Но это есть антинаучное представление о механизме распространения электромагнитной волны. Доказательством этого служит графическое представление электромагнитной волны в опыте.

t

На рис. 1б представлено экспериментальное распределение векторов напряженности электрического Е и магнитного Н полей в электромагнитной волне в квантованном пространстве-времени. Экспериментально в электромагнитной волне вихри не обнаружены. Кроме того, вектор напряженности электрического поля Е и вектор напряженности магнитного поля Н изменяются во времени t одновременно, без фазового сдвига на четверть периода УТ (или длины волны УХ), как на рис. 1а. Одновременность возникновения векторов Е и Н в электромагнитной волне исключает приоритет электрического или магнитного полей. Это означает, что электрическое поле не может родить поле магнитное в электромагнитной волне, и наоборот, констатируя ложность вихревой концепции. Электрическое и магнитное поле в электромагнитной волне существуют одновременно.

Чтобы возник вихрь в направление распространения электромагнитной волны векторы Е и Н должны иметь продольную компоненту как на рис. 1 а. Но в эксперименте продольная компонента отсутствует, электромагнитная волна содержит только поперечные векторы Е и Н. Это еще раз доказывает, что общепринятая вихревая концепция распространения электромагнитной волны, представленная на рис. 2а, не имеет под собой научной базы.

Казалось бы, что законы электромагнитной индукции открытые Фарадеем незыблемы: магнитное поле рождает круговое поле электрическое, и наоборот. И если взять колебательный контур из индуктивности и емкости, то в нем энергия электрического поля переходит в энергию магнитного, и наоборот, определяя сдвиг по фазе в УТ. Но почему в электромагнитной волне законы электромагнитной индукции не работают и энергия

электрического и магнитного полей не переходят друг в друга, а изменяются одновременно? Установлено, что объемная плотность энергии Wv в электромагнитной волне определяется двумя компонентами Е и Н [1]

Выражение (2) легко преобразуется в интенсивность потока S электромагнитного излучения (вектор Пойнтинга) в векторной форме, когда компоненты Е и Н существуют одновременно

S = Wv C o = |EH| (3)

Впервые ответ на поставленный вопрос об одновременности векторов Е и Н в электромагнитной волне был дан в теории УКС, когда открытие кванта пространства — времени (квантона) позволило рассматривать квантон как носитель сверхсильного электромагнитного взаимодействия (СЭВ), нарушение нулевого состояния (1) которого определяет условия формирования электромагнитной волны в вакууме [5-15]. Подробно это вопрос рассмотрен в обобщенной работе [1].

Удивляет то, что в течение всего 20 века, физики-теоретики, зная несоответствие эксперименту концепции вихревого распространения электромагнитной волны в вакууме, изображали вид, что в этом плане все хорошо, усложняя при этом математический аппарат электромагнитного поля, не зная причин проблемы. Даже введение четырехмерного векторного потенциала электромагнитного поля не приблизило решение данной проблемы не только в отношении классической электромагнитной волны, но и в отношении фотона, как определенного квантового состояния электромагнитной волны, наблюдая фотон как волну-корпускулу. Все названные проблемы решены в теории УКС, и их рассмотрение выходит за рамки данной статьи, основная тема которой определена фундаментальностью принципа относительно-абсолютного дуализма, связанного с реалиями светоносной среды. Поэтому необходимо напомнить основные положениями теории УКС в отношении светоносной среды.

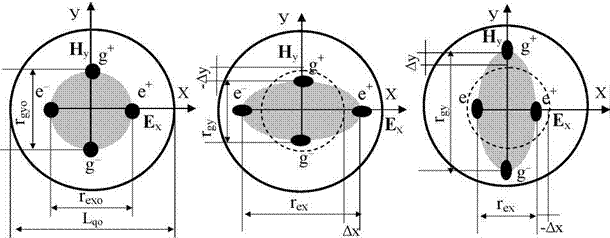
Реалии светоносной среды связаны с объединением электричества и магнетизма в электромагнетизм, как самостоятельную субстанцию квантованного пространства-времени, объединяющего одновременно пространство и время. На рис. 2а схематично и условно представлен в проекции квант пространства-времени (квантон) в равновесном (нулевом) состоянии. Полную информацию об объемной тетраэдрической структуре и свойствах квантона можно найти в работах [1,12-15]. В данном случае важно понять, что квантон объединяет электричество и магнетизм, и включает в себя четыре монопольных (не имеющих массы) элементарных заряда: два электрических (е+ и е-) и два магнитных (g+ и g-), связанных соотношением [1,12-15]:

g = Coe = 4,8 • 10 11 Дк (4)

где е=1,6’10~19 Кл — элементарный электрический заряд;

С0 — скорость света в невозмущенном гравитацией квантованном пространстве — времени ( в области слабого гравитационного поля Земли Со~ 3108 м/с). Магнитный заряда g измеряется в Дираках [Дк]= [Ам ], в честь Поля Дирака, который ввел в физику магнитный заряд (монополь Дирака) [29-31]. Объединение электричества и магнетизма внутри квантона обеспечивает сверхсильное электромагнитное взаимодействие (СЭВ), являющееся своеобразным «клеем» (глюоном), соединяя вместе две различные субстанции в одну. Экспериментально это подтверждается всеми электромагнитными процессами. Необходимо обратить внимание, что электрическая и магнитная оси квантона (рис. 2), связывающие соответствующие электрические и магнитные диполи, всегда остаются ортогональными друг другу, определяя ортогональность векторов Е и Н в электромагнитной волне, которая формируется в результате нарушения электромагнитного равновесия (нулевого состояния) квантованного пространства-времени.

Процесс квантования пространства включает заполнение его объема квантонами. Учитывая тетраэдрическую расстановку зарядов внутри квантона, ориентация квантонов в объеме определяется их случайным сцеплением, исключая какое-либо приоритетное направление электрических и магнитных осей квантонов в пространстве, и тем самым определяя анизотропные свойства пространства как однородной среды, электрически — и магнитонейтральной, но обладающего электрическими и магнитными свойствами, которые в совокупности учитываются электрической 80 и магнитной ц0 константами. С другой стороны, квантон представляет собой объемный электромагнитный упругий резонатор, своеобразные «электронные часы», задающие ход времени в пространстве, объединяя пространство и время в единую субстанцию квантованное пространство-время. Получается, что в каждой точке квантованного пространства идут свои часы, устанавливая темп протеканию электромагнитных процессов.

Невозбужденное состояние квантона (рис. 2а) определяет его нулевое равновесное состояние, когда расстояния Гехо и ^уо между центрами монопольных зарядов внутри квантона является величиной постоянной, и как показываю расчеты, связаны с диаметром Ьчо квантона соотношением [1]:

Lqo = 2Гехо = 2г§уо = 0,74 • 10-25 м (5)

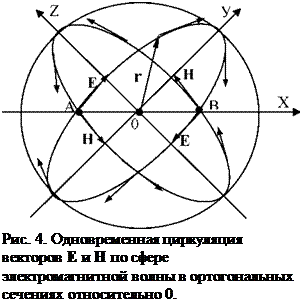
Необходимо обратить внимание на полную симметрию электричества и магнетизма внутри квантона, которая выражается в том, что в равновесном состоянии энергия We электрического поля взаимодействия электрических зарядов (е+ и е) эквивалентна энергии Wg магнитного поля взаимодействия магнитных зарядов (g+ и g-), то есть We = Wg с учетом (5):

Внутренняя аккумулированная энергия квантона определяется суммой электрической и магнитной энергий (7) и составляет 1,2′ 10~2 Дж, или порядка 1016 эВ. Учитывая высокую концентрацию квантонов (6), энергоемкость одного кубометра вакуума составляет порядка 10 Дж. Это колоссальная концентрация энергии, при активации которой возможно

рождение еще одной Вселенной вы результате Большого взрыва, когда вещественная часть Вселенной стала разворачиваться из сингулярного состояния соизмеримого с кубометром, который в масштабе Вселенной можно приять за точку. Но отсутствие в природе свободных магнитных зарядов и наличие некоторого избытка электрических, позволяет судить о том, сингулярное состоянии имело чисто электрическую природу в отсутствии магнитной компоненты. Такое состояние оказалось нестабильным, способным к активации. При наличии магнитной компоненты расщепить квантон на магнитные и электрические заряды не представляется возможным ввиду высочайшей его энергоемкости, представляя квантованное пространство-время, как самую стабильную субстанцию в природе.

Уравнение (7) дает соотношение электрических и магнитных параметров квантона, определяя их симметрию и устанавливая точное соотношение (4) между магнитным и электрическим элементарными зарядами. Полученное ранее Дираком соотношение зарядов некорректно, поскольку ведет к нарушению симметрии между электричеством и магнетизмом вакуума [28-30]. Примечательно то, что электрическая 80 и магнитная цо константы квантованного пространства-времени являются фундаментальными константами, действие которых проявляется на расстояниях значительно меньше диаметра квантона ~10_ 25 м, как и действие фундаментального закона Кулона для электрических и магнитных зарядов [1].

Выражения (4) и (7) есть форма записи уравнений Максвелла для вакуума, которые связывают электричество и магнетизм при электромагнитном возбуждении как отдельного квантона, так и их большой группы в квантованном пространстве-времени, когда в условиях прохождения электромагнитной волны через светоносную среду будет наблюдаться как деформационная, так и ориентационная поляризация квантона.

На рис. 2б представлен процесс деформационной поляризации квантона в результате его электромагнитного возбуждения, когда в течение полупериода волны, электрические монопольные заряды e внутри квантона растягивается по электрической оси Х, определяя их смещение Дх от нулевого состояния. При этом, магнитные заряды g одновременной смещаются к центру квантона на величину — Ду, в соответствии с (1), обеспечивая сохранение энергии квантона. В течение второго полупериода прохождения волны (рис. 2в), процесс поляризации квантона меняется на противоположный. Электрические заряды смещаются к центру квантона, а магнитные от центра, одновременно, также обеспечивая сохранение энергии квантона. То, что в электромагнитной волне соблюдаются законы сохранения энергии, подтверждается экспериментально по отсутствию в ней избыточной энергии. Волна переносит только энергию электромагнитного возбуждения [1,12-15].

Следует обратить внимание, что смещение магнитных зарядов к центру квантона (рис. 2б), ведет к увеличению энергии магнитного поля внутри фотона. При этом одновременной электрические заряды смещаются от центра фотона, уменьшая в эквиваленте энергию электрического поля внутри квантона, равную увеличению энергии магнитного поля, и обеспечивая тем самым, постоянство энергии квантона в электромагнитной волне. В квантоне наблюдается одновременный переход электрической энергии в магнитную, и наоборот. Изменение энергии внутри квантона (группы квантонов), в результате нарушения электромагнитного равновесия, внешне проявляется как одновременное индуцирование векторов Е и Н в квантованной среде и появление вектора Пойнтинга (3) определяющего перенос электромагнитной энергии (2) электромагнитной волной [1]. Длительность переходного энергетического процесса внутри квантона оценивается временем Тчо
прохождения электромагнитной волны через квантон, устанавливая период резонансного колебания квантона

То = — 2,5 • 10-34 с (8)

Co

Выражение (8) наглядно показывает, что дискретное пространство, которое характеризуется фундаментальной длиной Lqo, одновременной задает ход времени Тчо. Выражение (8) объединяет пространство и время как светоносную среду. Время Т^ (8) — это время самого быстротечного процесса в природе, несмотря на то, что на десять порядков больше планковского промежутка времени. С другой стороны, минимальное время Т^ позволяет говорить о квантованном характере времени, которое пропорционально ntTq^ где коэффициент nt представляет собой целое число от 1 до да. Если выбирать самый стабильный эталон времени, то лучшего чем квантон в природе эталона не существует. Но и это не идеальный эталон времени, поскольку зависит от возмущающего гравитационного потенциала, и в сильных гравитационных полях, такие часы будут отставать, а на поверхности черной дыры, вовсе остановятся.

Возвращаясь к анализу прохождения электромагнитной волны в квантованном пространстве-времени, необходимо отметить, что впервые удалось найти физические модели, которые реально доказывают существование токов электрического и магнитного смещения в вакууме. На это указывал еще Хевисайд. Впервые удалось найти физические модели, на основании которых получен аналитический вывод уравнений Максвелла [1,12­15]. Можно показать вывод уравнений Максвелла, дифференцируя (7), но нагляднее будет представить плотности токов электрического je и магнитного jg смещения в векторной форме через одинаковые скорости v смещения зарядов внутри квантона и квантовую плотность среды ро (6), учитывая ортогональность векторов je и jg

je = 2eP o v ^ jg = 2gPov

Подставляя (9) в (4) получаем соотношение между плотностями токов электрического и магнитного смещения в электромагнитной волне в вакууме в виде векторного произведения, в котором скорость света Со представляет собой вектор, ортогональный векторам je и jg

[Co je ]=- jg (10)

На рис. 3 представлен график электромагнитной волны в квантованном пространстве- времени в координатах токов смещения jg и je (10). Данный график ничем не отличается от графика на рис. 1б, когда параметры волны представлены векторами напряженности электрического Е и магнитного Н полей, связанные напрямую с плотностями токов смещения [1,12-15].

д E

о д t д H

д t

Наличие токов смещения jg и je в электромагнитной волне ведет к нарушению электромагнитного равновесия квантованного пространства-времени и одновременному появлению электрического и магнитного поля, представленного изменениями во времени t векторов Е и Н в (11), когда в электромагнитной волне одновременные параметры Е и Н не связаны с вихревым характером электромагнитной волны. Подставляя (11) в (10) устанавливаем четкое соотношение между параметрами Е и Н (с точкой) в векторной форме для гармонической электромагнитной волны [1,12-15].

е о [Со Е ]=-Н (12)

На рис. 1б уже был представлен график удовлетворяющий выражению (12). Зная параметр Е в электромагнитной волне, всегда можно вычислить параметр Н, и наоборот, используя (12). Это позволило уравнения Максвелла для вакуума свести всего к одному безроторному уравнению, которое можно представить в различной форме записи. Но это не означает, что безроторные уравнения (10), (11) и (12) электромагнитного поля в вакууме ставят под сомнение роторные уравнения Максвелла. Открытие квантона позволило обнаружить роторы электромагнитной сферической волны, но не там где их безуспешно искали, а на самой сфере вокруг источника излучения на любом расстоянии от антенны, минуя ближнюю область.

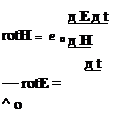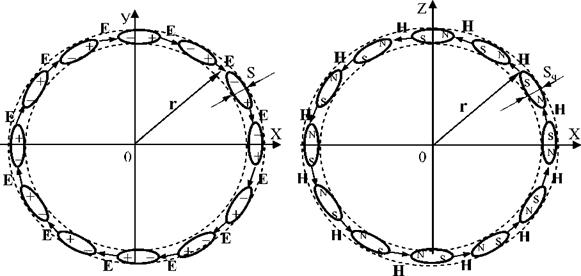
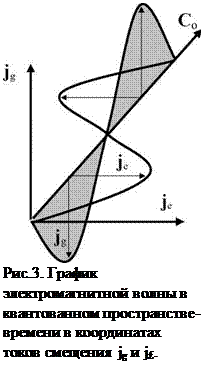
На рис. 4 представлена одновременная циркуляция векторов Е и Н по сфере электромагнитной волны в ортогональных сечениях относительно центра 0 излучения. Такая циркуляция описывается классическими роторными уравнениями Максвелла для вакуума

Классиков необходимо понимать глубже, чем понимали процессы они. В уравнениях Максвелла для электромагнитной волны в вакууме rotH и rotE существуют одновременно и не могут порождать друг друга. Это можно записать с учетом (10)

е о [С о rotH] = — rotE (14)

Выражение (14) учитывает ортогональность векторов Н, Е и С0, которая представлена в любой точке на сфере волны (рис. 4). Наглядно природа появления роторов Е и Н на сфере электромагнитной волны показана на рис. 5, когда электрические (а) и магнитные (б) диполи внутри квантона стараются замкнуться по сфере в результате ориентационной поляризации, устанавливая циркуляцию напряженности электрического Е (а) и магнитного Н (б) полей в электромагнитной волне относительно центра 0 излучения. Учитывая, что внутри квантона вектора Е и Н ортогональны друг другу, эта ортогональность соблюдается в каждой точке на сфере волны, позволяя выделить огромное количество роторов.

a) б) Рис. 5. Природа циркуляции напряженности электрического Е (а) и магнитного Н (б) полей в электромагнитной волне относительно 0.

В реальной электромагнитной волне, как показывают расчеты, смещение зарядов и угол поворота квантонов в результате деформационной и ориентационной поляризации, крайне малы, что указывает на сверхупругие свойства кантованного пространства-времени. Необходимо отметить, что электромагнитные процессы в вакууме носят статистический характер ввиду высокой концентрации квантонов (6) и тетраэдрической расстановки зарядов внутри квантона. Поэтому, уравнения Максвелла для электромагнитной волны в вакууме в любой форме записи (9)…(13) отражают среднестатистические параметры Е и Н в результате нарушения электромагнитного равновесия квантованного пространства-времени. Смещение зарядов Дх и Ду (1) внутри квантона очень просто связывает уравнения Максвелла и волновые уравнения электромагнитного поля [1].

Таким образом, краткое введение в электромагнитную структуру квантованного пространства-времени наглядно доказывает, что электромагнетизм является неотъемлемым свойством пространства-времени, которое служит не только переносчиком

электромагнитной волны, но и светоносной средой. Квантовые представления на природу электромагнитной волны могут быть перекинуты на структуру фотона, как особую квантовую форму электромагнитной волны, содержащую в себе роторы электрического и магнитного полей (14). Однако теория фотонного излучения и структура фотона представляют довольно сложный материал, выходящий за рамки данной темы, поэтому я коснусь только основополагающих положений фотонного излучения, опустив математические доказательства.

При зарождении фотона, например, в результате излучения орбитального электрона, рождение фотона начинается по сценарию сферической электромагнитной волны (рис. 4). Но поскольку эти процессы происходят очень быстро и переходят в область релятивистских скоростей, фотон успевает сформировать два ротора: электрический и магнитный, лежащих в ортогональных плоскостях поляризации. Учитывая, что на скорости света, роторы фотона не в состоянии раздуваться, как роторы сферической волны, структура фотона стабилизируется, представляя собой двухроторную частицу-волну в квантованном пространстве-времени. Теория относительности однозначно утверждает, что двухроторный фотон раздуваться не может, как классическая сферическая волна. Но фотон, как квантовый сгусток электромагнитной энергии волнового типа отличается от сферической волны тем, что энергия hv фотона пропорциональна частоте v его электромагнитного поля (h —
постоянная Планка). Это имеет строгое доказательство в теории УКС и ТЕЭП, но не рассматривается в данной работе.

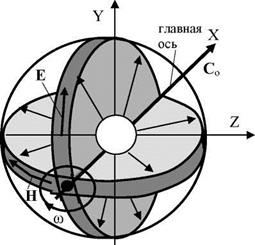Рис. 6. Двухроторная структура
низкоэнергетического фотона
излучаемого орбитальным
электроном.

На рис. 6 представлена упрощенная схема двухроторного низкоэнергетического фотона, циркуляция векторов напряженности электрического Е и магнитного Н полей лежит в ортогональных плоскостях поляризации в соответствии с уравнениями Максвелла. Фотон имеет главную ось, в направлении которой он движется в пространстве со скоростью света Со, и вокруг которой возможно вращение плоскостей поляризации в оптических средах в результате взаимодействия роторных полей с решеткой оптических сред. В отличие от сферической электромагнитной волны или плоской волны, имеющей только поперечные вектора Е и Н, роторные поля фотона имеют продольные компоненты Е и Н, и только на главной оси векторы Е и Н остаются поперечными к направлению вектора скорости фотона. Сегодня теория УКС и ТЕЭП располагает полным математическим аппаратом исследования структуру и уникальных свойств фотона как частицы-волны.

Анализ взаимодействия роторных полей фотона с решеткой оптических сред, шаг которой намного меньше длины волны электромагнитного поля фотона, показывает, что это взаимодействие носит статистический характер, когда фотон способен захватывать своим полем периодически некоторые атомные ядра решетки, обеспечивая вращение плоскостей поляризации и волновую траекторию движения фотона в оптической среде. В общем случае, при движении фотона в оптической среде фотон проявляет волновые свойства дважды:

1. Циркуляция векторов напряженности электрического Е и магнитного Н полей в роторах фотона осуществляет волновой перенос электромагнитной энергии фотона со скоростью света С0 благодаря наличию светоносной среды, то есть квантованного пространства-времени. В вакууме траектория фотона представляет прямую линию.

2. В оптических средах периодическое взаимодействие роторных полей фотона с полями решетки оптической среды периодически отклоняет траекторию фотона от прямой линии в светоносной среде, определяя его волновую траекторию. Движение по волновой траектории со скоростью света Со, создает впечатление, что в оптических средах скорость света замедляется, поскольку время движения по волновой траектории больше времени движения по прямой линии.

Проблема замедления скорости света в оптических средах не объясняется их диэлектрическими свойствами, которые не согласуются с коэффициентом преломления среды, и представляет серьезную проблему современной физики. Если рассматривать оптическую среду как среду светоносную, то замедление скорости света в оптической среде по сравнению с вакуумом не подчиняется логическому осмыслению, поскольку вакуум не считается светоносной средой. Все становится на места свои, когда вакууму возвращены свойства светоносной среды, которая обеспечивает волновой перенос фотона со скоростью

света Со. В оптической среде, внутри которой размещена светоносная среда, скорость фотона также определяется волновой скоростью света Со в светоносной среде. Искривляется только траектория, превращаясь из прямой линии, в волновую траекторию.

фотона в оптической среде ломаной линией.

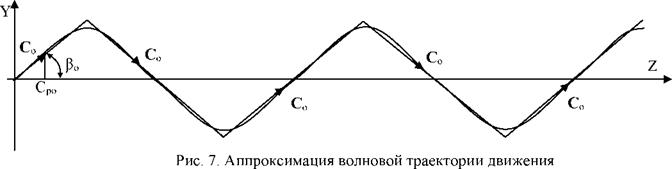
На рис. 7 представлена аппроксимация волновой траектории движения фотона в оптической среде периодической ломаной линией. Всегда можно подобрать такую ломаную линию, которая по своей длине была бы эквивалентна длине волновой траектории фотона, определяя одинаковое время прохождение фотона в оптической среде. Анализ движения фотона по периодической ломаной траектории значительно упрощает расчетный аппарат. Как видно, вектор скорости света С0 при движении фотона в оптической среде по волновой линии периодически меняет свое направление относительно прямой линии (оси Z), оставаясь по модулю постоянной величиной, то есть Со=СОП8Й Постоянство модуля скорости света в оптической среде привязано к среде светоносной, то есть к квантованному пространству — времени, подчиняясь условиям специальной теории относительности (СТО) Эйнштейна.

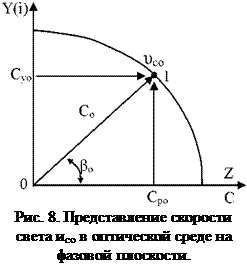
На рис. 8 скорость света в оптической среде представлена на фазовой (комплексной) плоскости как комплексная скорость света 0со в точке 1, которая определяется ее модулем Со и углом (аргументом) ро, где i — мнимая единица, е =2,71…

Зсо = Сро + iC уо = Со eiPo (15)

Со = const (16)

Модуль комплексной скорости Со (16) связан теоремой Пифагора с действительной фазовой скоростью Сро фотона по оси Z и мнимой скоростью Суо по оси Y в (15), представляя Со двумя компонентами: продольной Сро и поперечной Суо, при этом индексы (о) означают, что параметры скоростей относятся к неподвижной относительно наблюдателя оптической среде

С2 = С ро + С 2о = const (17)

Сравнивая углы ро на рис. 8 и рис. 7, нетрудно убедится, что это один и тот же угол, который определяет показатель преломления no оптической среды

Co 1

no = =—— Г — (18)

Cpo cos Po

В движущихся оптических средах с относительной скоростью vz в направлении оси Z свет не увлекается оптической средой, даже частично, поскольку скорость света привязана к светоносной среде и остается величиной постоянной (16). В знаменитом опыте Физо, частично увлечение света является кажущемся эффектом, поскольку на самом деле меняется показатель преломления no (18) и угол ро (15) оптической среды, на новые параметры: nv, и pv, определяя новую фазовую скорость Срт света в движущейся среде (индекс (v) обозначает параметры в движущейся среде)

Комплексная скорость света $с,^ в движущейся среде со скоростью vz будет отличаться от комплексной скорости 0со (15) в неподвижной среде при постоянстве модуля Со (16)

= Opv + iC уv = Со elPv (20)

Увеличение фазовой скорости Срт света в движущейся среде при постоянстве Со, возможно только за счет уменьшения мнимой компоненты С^ комплексной скорости 9^

(20). Поскольку модуль скорости Со определяется из суммы квадратов скоростей (17), то простое арифметическое сложение скоростей Сро и vz при определении фазовой скорости Срт, будет некорректным и приведет к серьезным погрешностям. Сложение скоростей определяется из суммы квадратов продольной Срт и поперечной С^ компонент.

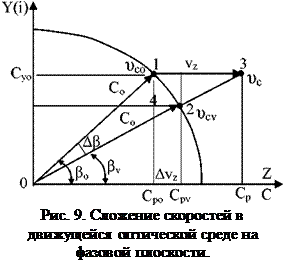
На рис. 9 представлено графическое сложение скоростей Сро и vz на комплексной плоскости, при условии когда модуль скорости свете Со остается постоянным в светоносной среде. В неподвижной оптической среде комплексная скорость света 9со (15) в точке 1 определена аргументом ро при условии (16). В подвижной оптической среде комплексная скорость света 9с,^ (20) в точке 2 определена аргументом pv при условии (16). Если бы

скорость света Со не была бы привязана к светоносной среде, а была бы привязана к среде оптической как Сро, то при полном увлечении света движущейся оптической средой, суммарная скорость Ср определялась бы арифметической суммой:

Cp = Cpo ± vz (21)

Но выражение (21) не соответствует результатам экспериментальных измерений. В опыте Физо фазовая скорость света Срт в движущейся среде определяется формулой, в которую входит приращение скорости Avz<vz

Cpv = Cpo ±Avz < Cp (22)

Выражение (22) обычно ошибочно связывают с тем, что в движущейся среде наблюдается частичное увлечение света. Если провести векторное сложение скоростей света Со и скорости vz движения оптической среды, то вектор суммарной скорости ис в точке 3 превысит скорость света Со, что в принципе невозможно поскольку скорость света Со привязана к светоносной среде.

Чтобы правильно определить фазовую скорость света Cpv в движущейся среде ее необходимо искать как проекцию на ось Z, исходя из комплексной скорости (20) в точке

2 (рис. 9). Для этого в выражение (22) необходимо ввести истинное приращение фазовой скорости Avz, как векторную величину, которая находится из треугольников 1-2-3 и 1-2-4, исходя из их подобия через угол Ро с учетом (18)

Формула (23) является приближенной, поскольку дуга окружности 1-2 в треугольнике

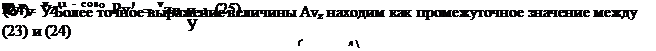1-2-3 искажает его углы. Поэтому, выражая приближенную формулу:

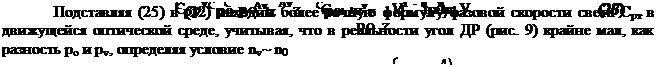Подставляя (23) в (22) находим фазовую скорость света Срт в движущейся оптической среде в первом приближении, формула которой хорошо известна в физике [24]

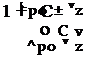С учетом (18) и (19) выражение (27) легко преобразуется в известное выражение для сложения скоростей в специальной теории относительности (СТО) Эйнштейна при условии постоянства скорости света Со [32]

Все полученные выше формулы (26), (27), (28) справедливы для фазовой скорости света в движущейся оптической среде при условии наличия светоносной среды, скорость света Со в которой является величиной постоянной. Постоянство скорости света (16) является базисом специальной теории относительности (СТО). В движущейся оптической среде постоянство скорости света Со возможно только при наличии светоносной среды. Поэтому формула сложения скоростей (26) в СТО полностью подходит для определения фазовой скорости света Срт в движущихся оптических средах, поскольку определяется не арифметической суммой, а исходя и суммы квадратов продольной и поперечной компонент скоростей при движении фотона по волновой траектории в оптической среде, в том числе при ее относительном движении. Это задается условиями постоянства скорости света (16) в светоносной среде.

То, что фазовая скорость света оказалась меньше арифметической суммы скоростей, впервые было обнаружено в опыте Физо, но правильное объяснение данного эффекта
удалось дать только в теории УКС, когда в оптической среде фотон движется по волновой траектории, а при относительном движении оптической среды изменяется показатель ее преломления. Создавая теорию фотонного излучения и самого фотона, которая не столь простая, и не входит в материалы данной статьи, необходимо отметить, что, несмотря на статистический характер поведения фотона в оптической среде, его параметры вполне предсказуемы, поскольку начинают проявляться причины самих явлений. Квантовая теория с открытием кванта пространства-времени (квантона) и сверхсильного электромагнитного взаимодействия (СЭВ) становится детерминированной, как настаивал на этом Эйнштейн.

Краткий анализ квантованного пространства-времени позволяет вернуть физике концепцию светоносной среды. Это расчищает заторы на пути к квантовой теории гравитации (КТГ), которая целиком простроена на реалиях упругой квантованной среды способной к сжатию и растяжению. Электромагнитные взаимодействия характеризуются противоположным смещением зарядов квантоне (1), когда сближение электрических зарядов связано с одновременным удалением магнитных зарядов, обеспечивая сохранение энергии квантона. При этом концентрация квантонов единице объема остается неизменной. Гравитационные взаимодействия также характеризуются одновременным смещением (1) зарядов в квантоне, только в одну сторону, на сближение или удалении друг от друга, равномерно сжимая или растягивая квантон, и изменяя его энергию. Как отмечалось, в данной работе не рассматриваются процессы смещения зарядов внутри квантона в результате гравитационных взаимодействий. Важно, то, что гравитация характеризуется сжатием или растяжением квантонов, изменяя их концентрацию в единице объема, которая ведет к градиентному перераспределению квантовой плотности среды в квантованном пространстве-времени. Именно через квантон происходит объединение электромагнетизма и гравитации, когда в одних случаях проявляются электромагнитные взаимодействия, а в других — гравитационные, как свойства единого поля — носителя сверхсильных электромагнитных взаимодействий (СЭВ).

Комментарии запрещены.