Бурение грунтовых зондов, установка энергетических колодцев

В практике проведения геолого-технологических исследо­ваний данные о температуре ПЖ на выходе из скважины используются довольно широко как за рубежом, так и у нас в стране для выделения зон АВПД [49, 81, 169], выделения проницаемых интервалов [81, 182], определения температу­ры на забое скважины [79, 127]. Однако серьезных теорети­ческих работ, связывающих температуру ПЖ на выходе из скважины с забойными условиями с целью получения обос­нования ее геологической информативности, в литературе не встречается.

Э. Е. Лукьяновым совместно с А. И. Филипповым (Башгосу — ниверситет) сделана попытка восполнить этот пробел.

температура ПЖ в бурильных трубах, К; температура в затрубном пространстве, К;

Введем модель, показанную на рис. 5.15, и обозначения: Тх — т2~ с — р — к, — к2- г0 — а —

Дж

удельная теплоемкость ПЖ, ————— ;

К • кг

кг

плотность ПЖ, —3-;

м

скорость движения ПЖ в бурильных трубах, м/с; скорость движения ПЖ в затрубье, м/с; внутренний радиус бурильных труб, м; коэффициент теплообмена бурильных труб с за-

Вт

трубьем, — м2 к;

Яг —

величина теплового потока в горные породы (из Вт

горных пород), — м

Предположим, что: — расход ПЖ в бурильных трубах равен расходу ПЖ в за — трубье (поглощение или приток в скважину отсутствуют); — теплообмен по затрубно — му пространству осуществляет­ся по закону Ньютона; — тепловыделения за счет работы долота на забое пренеб­режимо малы; — частицы выбуриваемых пород (шмала) не изменяют за­метно температуру потока. Составляя уравнение балан­са тепловой энергии для пото­ка жидкости в бурильной трубе и затрубном пространстве, при­ходим к уравнениям:

радиус скважины, м.

Л — ‘VI і | СІї V % г* £

Рис. 5.15

CpdTvS[dz + CpV[S[dtdTl +

+а(Г1 — Т2) = О, (5А2)

Срс1Т252с11 — CpV2S1dtdT2 —

— 2лг0а(Г| — Т2) + q(z)2лRdzdt = 0. (5.43)

Из (5.42) и (5.43) приходим к уравнениям температуры пото­ков жидкости в трубах и затрубном пространстве:

dT dT^ 2лг0а

+^+-гг<г’-Гг)-°’ ^

5, ^ ^ + ^(Г, — Г,) + М,(г) . 0.

а’г ог Ср Ср

(5.45)

Далее введем характерные параметры — время бурения т и полную глубину бурения (глубину скважины) Н.

Тогда, складывая (5.44) и (5.45), найдем:

у-, <1(Т2 — ТХ). 2лг0

о —^ (5.4б)

где 0 = КД = У252 — расход ПЖ, л/с.

Последнее равенство по сути дела означает, что:

— разность температур не зависит от теплообмена между тру­бами и затрубьем, а определяется только полным количеством получаемого или отданного тепла;

— разность температур не зависит от соотношения скоростей в трубах и затрубном пространстве.

Последние два вывода положим в основу рассматриваемой теории.

Для поиска решения положим, что Тх и Т2 на забое равны. При этом мы пренебрегаем выделением тепла за счет работы долота.

Тогда из (5.46) получим:

(5.47)

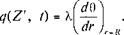Величина радиального теплового потока выражается через гра­диент температуры (©) в окружающих породах и коэффициент теплопроводности Х[Вт/(М • °С)]:

(5.48)

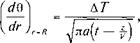Можно показать, что хорошим приближением к расчету гра­диента температуры в окружающих породах вблизи стенки сква­жины является выражение

(5.49)

где АТ — разность геотермической и скважинной темпе­ратур, К;

а — коэффициент температуропроводности горных пород, м2/с;

г — глубина точки наблюдения (текущая координа­та), м;

(/ — 7) — время после вскрытия интервала с координа-

той I, С.

Полная математическая постановка задачи весьма сложна, по­этому при принятых допущениях достаточно рассмотреть сле­дующую упрощенную задачу:

2л ХЯ

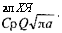(5.50)

Обозначим (3 =

При начальном условии Т2/1 = К/ = Г,.

(5.51)

-2РМ’-7

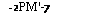Решение задачи (5.50) — (5.51) легко получить классически­ми методами. Путем непосредственной подстановки можно убе­диться, что оно имеет следующий вид

т2 = Л + Т0 + (Тх —Гг — 7’0)схр

(I1 • ехр

V

-2(3 Ум —

V

—Г Б ехр

2рК./

(5.52)

На устье скважины (г = 0) из (5.52) получим выражение для расчета температуры выходящей из скважины промывочной жидкости

Т2 /г.„ = Т0+(Т,- Г0)ехр(2|з к77) +

Г

1 — ехр(—2|ЗК-/7)|

(5.53)

2р2К

Отсюда легко найти выражение для скорости изменения тем­пературы на устье скважины во времени

Тс м

-2

= 1,5-10

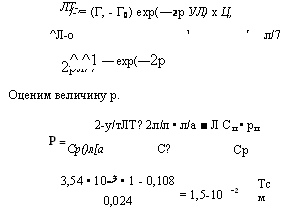
2рл/7 Оценим величину р. 2-у/тЛТ? 2л/л • л/а ■ Л Сп • рп

/- = (Г, — Г0) ехр(—2р УЛ) х Ц, ^Л-о 1 ‘ л/7 ^ ^1 — ехр(—2р

Ср()л[а С? 3,54 • 10~3 • 1 — 0,108 0,024

ЛТ-,

Р =

Ср

(5.54)

Учитывая, что скорость бурения (в системе СИ), а тем более про­изведение р • V« 1, первое слагаемое в (5.54) можно опустить.

Тогда

(5.55)

Это выражение по сути дела рашает поставленную задачу.

Из выражения (5.55) следует, что скорость изменения тем­пературы ПЖ на выходе из скважины во времени зависит от величины геотермического градиента, скорости бурения, рас­хода промывочной жидкости и средней температуропроводно­сти пород, окружающих скважину (последние две величины входят в (3).

Для того чтобы выяснить, какие из рассматриваемых величин оказывают основное влияние, рассмотрим асимптотику реше­ния для малых времен / < 1000 часов, охватывающих практиче­ски весь период бурения скважины.

Воспользуемся разложением: е^х = 1 — х, где х < 0,1.

Тогда

(5.56)

Выражение (5.56) позволяет указать на основной вклад в измене­ние температуры ПЖ на выходе из скважины (при сделанных допу­щениях) геотермического градиента и скорости проходки.

с1Т,

В случае перенесения кривой на ось глубин путем при­вязки ее к соответствующим глубинам с учетом «отставания» (за­держки сигнала на время перемещения его по каналу связи) вы­ражение (5.56) преобразуется в

(5.57)

Таким образом, при отсутствии поглощения или притока вне интервалов проницаемых пластов скорость изменения разно­сти температур ПЖ на входе и выходе из скважины связана в первую очередь с петрофизическими особенностями разреза, а именно с геотермическим градиентом и буримостыо породы, а изменение разности температур ПЖ на входе и выходе в функ­ции углубления скважины отражает изменение геотермическо­го градиента вскрываемого разреза, т. е. несет геологическую ин­формацию.

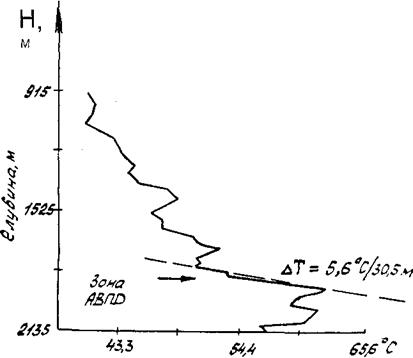
Именно на этом основана методика выделения зон АВПД по температуре ПЖ на выходе из скважины, широко применяемая за рубежом [49, 169].

В основу данной методики положена модель К. Р. Льюиса и С. К. Роуза [169], устанавливающая взаимосвязь между повы­шенными давлениями и увеличенными пластовыми температу­рами на основе принципов теплового поля. Высокопористые гли­нистые сланцы с повышенным давлением, согласно этой моде­ли, ведут себя как «тепловые барьеры», локально обусловливая увеличение геотермического градиента. Изменения температур­ных градиентов на выкидной линии до 18,2°С/100м наблюда­лись до и (или) во время вскрытия интервалов повышенных дав­лений (рис. 5.16).

Р. X. Джонс констатировал [169], что геотермические гради­енты велики в глинистых пластах, перекрывающих коллекторы, и очень сильно уменьшены в водоносных пластах.

Это дает основание выделять коллекторы по температуре на выходе из скважины непосредственно в процессе бурения.

Однако до сих пор из-за отсутствия надежных теоретических обоснований изменение температуры на выходе из скважины для выделения коллекторов не используется, хотя участки с отрица­тельным градиентом температуры, как правило, приурочивают­ся к интервалам с повышенной пористостью и нормальным дав­лением.

При решении же задачи выделения зон АВПД эти участки не берутся во внимание, т. к. основной задачей является выделение момента резкого увеличения градиента температуры на выходе из скважины (рис. 5.16).

Одной из основных причин этого является трудность объяс­нения наличия отрицательных градиентов при непрерывном росте температуры с глубиной. В этом случае необходимо допустить уменьшение температуры горных пород под долотом на отдель­ных участках разреза относительно вышележащих пород за счет нарушения естественного теплового режима при вскрытии пла­ста-коллектора.

Рис. 5.16. Выделение зоны АВПД по температуре на вы­ходе из скважины [169]

Уравнения (5,56) и (5.57) получены при допущении, что потерь промывочной жидкости в скважине не происходит, что характер­но для непроницаемых участков разреза. Наличие в разрезе высо­копроницаемых коллекторов существенно искажает поведение тем­пературы на выходе из скважины, однако эти искажения, как от­мечалось ранее [81], не являются дезинформацией, а содержат в себе полезную информацию о реальных изменениях термобари­ческих условий при вскрытии пласта.

На сегодняшний день факт опережающего проникновения фильтрата ПЖ под долото можно считать окончательно уста­новленным [177] практически во всех случаях вскрытия пла­ста при применении ПЖ на водной основе. Это обстоятельст­во позволяет построить модель вскрытия, для которой харак-

терно наличие под долотом зоны, промытой более холодным (по отношению к первоначальной температуре горной поро­ды) фильтратом ГТЖ, что неизбежно снижает геотермический градиент породы под долотом за счет понижения температуры пласта.

Только этим можно объяснить уменьшение геотермического градиента в пластах-коллекторах, т. к. оценка эффекта снижения температуры ПЖ на выходе из скважины за счет поглощения ПЖ с интенсивностью 10 л/с при реальном времени «отстава­ния» / = 2500 с и реальной скорости проходки -30 м/ч не превы­шает значений 0, ГС/м, тогда как реально снижение достигает значений 5°С/м.

С учетом фазовой проницаемости и теплофизических свойств флюидов [177] следует ожидать при прочих равных условиях наи­большего эффекта при выделении газонасыщенных и водонасы­щенных коллекторов и меньшего эффекта при выделении неф­тенасыщенных коллекторов.

В целом же эффект выделения проницаемого коллектора по из­менению (уменьшению) температуры ПЖ на выходе из скважины будет зависеть от степени снижения первоначальной температуры пласта, т. е. в конечном счете от количества фильтрата ПЖ, прошед­шего через поровое пространство пласта. Количество же профильт­ровавшейся жидкости обусловливается перепадом давления между гидростатическим и пластовым, фильтрационными свойствами по­роды и свойствами флюида, насыщающего пласт-коллектор [81, 177].

Поэтому величина отрицательной аномалии градиент-термо­граммы определенным образом связана с фильтрационными свой­ствами изучаемого пласта-коллектора.

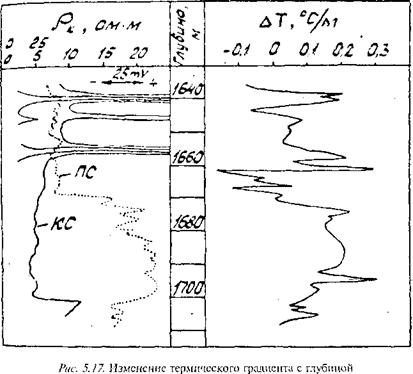
На рис. 5.17 приводится фрагмент градиент-термограммы ПЖ на выходе из скважины в сопоставлении с данными ГИС.

Продолжением работы в данном направлении должно стать нахождение аналитической зависимости между величиной ано­малии и фильтрационными характеристиками вскрываемого пла — ста-коллектора.

Комментарии запрещены.