Бурение грунтовых зондов, установка энергетических колодцев

Движение материальной точки будет несвободным, когда вслед­ствие наложенных связей она вынуждена двигаться по заданной поверхности или кривой. Рассмотрим движение точки по кривой.

144

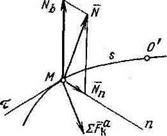
; Рис. 6.1. Расчетная схема для несвободного движения точки

Расчетная схема для этого случая показана на рис. 6.1. Матери­альная точка М движется по заданной гладкой неподвижной кривой под действием активных сил У Ft. Поскольку на точку наложена связь, возникнет реакция связи N. Положение точки в данный момент времени характеризуется криволинейной координатой s. Запишем второй закон динамики для несвободной материальной точки

(6.67)

Теперь спроецируем это равенство на оси естественного трехгран­ника (см. раздел 5.1). В результате получим следующие дифферен­циальные уравнения движения точки по заданной кривой:

(6.68)

mw„ — mv 21 р — £ FI, + NK, тщ — 0 = £ F& + N.

Уравнение (6.68) не содержит неизвестной реакции N и позволяет непосредственно определить закон движения точки вдоль кривой, ; т. е. зависимость х =/(/). Этим уравнением можно пользоваться и в случае, когда кривая не является гладкой, присоединив к силам F*T силу трения FTp. Но так как F™ = 7vT. то в этом случае в уравнение I (6.68) через силу трения войдет еще и реакция N.

I Уравнения (6.69) служат для определения реакции связи N. Из [ уравнений видно, .что при криволинейном движении динамическом ; реакция в отличие от статической, кроме действующих сил и вида, связи, зависит еще от скорости. Эту скорость (если она не задана) ‘ можно найти, проинтегрировав уравнение (6.68), или, что обычно г проще, с помощью теоремы об изменении кинетической энергии р точки (6.54).

Теперь рассмотрим динамику относительно движения точки. ‘ Второй закон динамики и полученные из него все приведенные выше ; уравнения и теоремы верны только для так называемого абсолютного. 10 3477 ‘ 145

движения точки, т. е. по отношению к инерциальной («неподвижной») системе отсчета. Рассмотрим материальную точку, движущуюся под действием активных сил Будем изучать движение этой точки

по отношению к подвижным осям, которые перемещаются относи­тельно неподвижных. Для абсолютного движения точки с учетом уравнения (5.48) второй закон динамики может быть записан в виде

я™’ пер + ‘Ий’™,+пт = (6.69)

Запишем это уравнение следующим образом:

w’oth = £FE+(wi- w’ncp)+(- mwk). (6.70)

Введем обозначения

ши’пер F пср, ши’к Fkop — (6.71)

Эти две фиктивные силы назовем переносной и кориолисовой силами инерции. Тогда уравнение (6.70) примет вид

+ f “„о. (6.72)

Уравнение (6.72) выражает основной закон динамики для относитель­ного движения точки. Отсюда можно заключить, что все уравнения и теоремы механики для относительного движения точки составляются так же, как уравнения абсолютного движения, если при этом к действующим на точку силам прибавить переносную и кориолисову силы инерции.

Здесь можно отметить ряд частных случаев. Если подвижные оси

движутся поступательно, то F“op = 0. Если подвижные оси перемещаются поступательно, равномерно и прямолинейно, то F„cp = 0 и F“„p = 0. Если точка по отношению к подвижным осям находится в покое, то иотн=0 и Готн = 0. Тогда уравнение относительного равновесия запишется в виде

IF| + F^cp = 0. (6.73)

Комментарии запрещены.