Бурение грунтовых зондов, установка энергетических колодцев

В практике разведочного бурения используют лебедки, в которых укладка канатов предусмотрена в несколько слоев. Укладку каната в три, четыре слоя и более применяют не только на станках ударно-канатного бурения, где общая длина укладываемого каната может достигать 300 м и более, но и на станках колонкового бурения, где эта длина составляет менее 50 м. Существуют подъемные 114

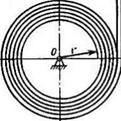
Рис. 5.8. Схема грузоподъемного устрой­ства со спиральной намоткой каната на барабан

d

С

устройства, в которых канат укладывают по спирали. Иногда таким образом наматывают резиновые шланги и другие гибкие элементы.

Особенность всех подъемных приспособлений такого рода состоит в том, что радиус намотки меняется по тому или иному закону, вследствие чего кинематические характеристики точек наматываемого каната также претерпевают соответствующие изменения. Подобные задачи решают с применением кинематических соотношений враща­тельного движения твердого тела.

Рассмотрим две задачи, в которых исследуется движение одного приспособления. Однако в первой задаче канат наматывается на барабан, во второй — сматывается.

Исследуемое грузоподъемное устройство показано на рис. 5.8. Будем считать, что канат наматывается по спирали. Подобная намотка обеспечивается устройством на барабане реборд. В первой задаче дано: угловая частота вращения барабана со, начальный радиус барабана г, диаметр каната d. Определить скорость движения каната в функции угла поворота барабана и в функции времени, закон движения поднимаемого груза С, касательное, нормальное и полное ускорения точек наматываемого на барабан каната в функции времени. На основании рис. 5.8 легко установить, что за один поворот барабана его радиус изменится на величину с/. С учетом этого можно записать

(5.51)

р = / +(фс//2л).

где р—текущий радиус намотки каната; ср — угол поворота барабана.

Тогда линейную скорость каната при любом значении угла можно определить по формуле

(5.52)

Но ф = <ot, следовательно

/ ~

= (о( г+—— ). (5.53)

J

Определим касательное ускорение точек каната wI=dv/dt—(H’idl 2л. (5.54)

Нормальное ускорение точек каната

/

и„ = (о2 (/-+ — |, (5.55)

V /

Г ‘4л

а полное ускорение

(5.56)

Закон движения груза С определится по формуле

s=v0t + nt2/2, (5.57)

где v0 —га>—начальная скорость движения груза, или

г соrt со2 dt2 … .

—’■—~л—• (5 58)

— 2 4л

Пример I. Предположим, наматывается канат длиной 5=40 м, / =0,1 м, d=0,02 м и со=5 с-1. Необходимо установить время наматывания каната, максимальный радиус намотанного • каиага, а также линейную скорость и полное ускорение точки каната в конце наматывания.

Первоначально определим время намотки каната по формуле (5.58) < = 26,03 с, а затем максимальный радиус намотанного каната /■П1ах=0,51 м, касательное и’,=0,08 м >с-2 и нормальное ускорение и>„= 12,86 м-с-2 по формулам (5.51), (5.54) и (5.55) соответственно. Полное ускорение будет равно нормальному ускорению.

Теперь рассмотрим вторую задачу. На барабан намотано п витков. В начальный момент (<о = 0), когда ф = 0 и тг0 = 0, груз начинает опускаться в скважину с. ускорением vrT. Требуется определить закон изменения угловой скорости барабана и полного ускорения точки каната на барабане в функции времени.

Скорость груза (или скорость точки каната на барабане) будет составлять

v—wrt. (5.59)

Радиус R сматывания каната в зависимости от угла поворота барабана определится выражением

R = r+nd—(<f>d/2n). (5.60)

Тогда угловая скорость может быть найдена по формуле

w. t

(0=— [4] (5.60

r+nd—(tpd/2п)

Но J ф = o’ldt, тогда

d ф=——- —-— dt. (5.62)

r+nd— (q>d/2n)

Произведем разделение переменных и проинтегрируем выражение (5.65) в пределах от 0 до ф:

Ф ^r+nd—^^j — |"нtdt. о о

В результате получим

~-Ф(г+и</) + —==0.

Решая последнее уравнение относительно ф, найдем 2 n(r+nd) I

(5.63)

2n(r+nd)V 2itwxl2

d J J

—V

Обозначим

2n(r+nd)/d=A, 2nwx/d=B.

Подставляя эти значения в (5.63), имеем

<p~A-(A2-Bt2)l/2. (5.64)

Отсюда легко найти

IV, I

. со=————- —г————————- ! .——————————————— (5.65)

r+nd-—[A-(A2-Bt2)ll4

2я

При этом нормальное ускорение w2t2

w„ = I. (5.66)

s-te,/2/2,

1=6,23 с. Вычислим постоянные /1 = 125,6 и В= 314. Тогда угловая скорость ш= 34,9 с’ ‘, а нормальное ускорение ir„=223,4 м-с~2.

Поскольку нормальное ускорение существенно больше касательного, полное ускорение будет равно нормальному ускорению точек каната.

Представленный пример дает убедительное объяснение часто встречающегося в практике производства буровых работ явления самопроизвольного разматывания каната на барабане при спуске снаряда в скважине. Бурильщик, как правило, стремится спустить снаряд в скважину возможно быстрее. Однако, встретив сопротив­ление, снаряд может приостановить свое движение. Если бурильщик вовремя не притормозит лебедку, то весь канат быстро смотается с барабана, витки его перепутаются и последующая укладка каната потребует определенного времени. Это объясняется не только тем, что лебедка по инерции продолжает вращаться, но и тем, что на лишенный натяжения канат уже не действуют динамические реакции связей. Центробежные силы «отбрасывают» канат от барабана. Например, чтобы удержать участок каната массой 0,5 кг на барабане, нужно приложить к нему силу больше 110 Н.

Комментарии запрещены.