Бурение грунтовых зондов, установка энергетических колодцев

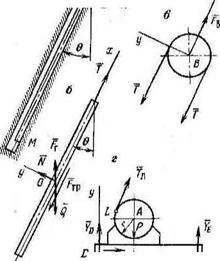
Колонна бурильных труб МС, находящаяся в наклонной скважине j (рис. 4.4, а), равномерно поднимается лебедкой А с помощью каната СВ, перекинутого через блок В мачты. Определить натяжение каната, усилие на мачту и реакции опор, возникающих в точках крепления j станка D и Е.

В учебных задачах по теоретической механике исходные данные I обычно приводятся сразу. В задачах, аналогичных представленной, I эти данные еще требуется установить. В соответствии с рекомен­дациями раздела 4.1 первоначально следовало бы в масштабе, по возможности,. наиболее детально изобразить на чертеже полную конструктивную схему рассматриваемой системы тел и показать все действующие на нее силы. Однако этот этап мы опустим, равно как и следующий, связанный с определением ориентировочно заданных величин. При реальных расчетах желательно выполнить работы, 1 относящиеся к обоим этапам. В данной задаче мы сразу перейдем [3] к идеализации расчетной схемы, одновременно выполняя операции ] предыдущих двух этапов.

Введем следующие допущения. Ось скважины строго прямолинейна и направлена под углом 0 к вертикали *. Скважина заполнена глинистым раствором с удельным весом yi — Колонна бурильных труб также строго прямолинейна, длина колонны Н, сила тяжести 1 м q, плотность материала труб р. Скважина пробурена в однородном геологическом разрезе, коэффициент трения материала труб о горную породу соответствует /. Наличие колонковой трубы на нижнем конце

Рис. 4.4. Конструктивная схема | и схема усилий, действующих при извлечении колонны бу­рильных труб из наклонной скважины

колонны труб не учитывается, гидравлическими сопротивлениями при подъеме колонны также пренебрегаем. Сопротивления в блоке отсут­ствуют. Обе ветви каната параллельны друг другу. Радиус барабана г лебедки постоянен. Два последних допущения являются фиксацией двух неопределенных (изменяющихся) величин, определяющих направ­ление и точку приложения силы, действующей на лебедку со стороны каната. Эти величины меняются вследствие наматывания каната на барабан лебедки. Станок к основанию прикреплен болтами в точках D и Е. Отрезки DE—l, DK^a, КА = Ь. Линия LB проходит через точку D. Сила тяжести станка Р действует вдоль линии А К.

Поскольку станок жестко прикреплен к основанию, в точках D и Е возникает по три неизвестных реактивных силовых фактора: реакции вдоль оси х и у и реактивный момент. Если рассматривать равновесие только бурового станка и считать, что усилие Тл (рис. 4.4, г) уже определено, то окажется, что в полученной системе сил содержится шесть неизвестных величин, тогда как для плоской произвольной системы сил можно составить только три уравнения статики.

Такая система сил трижды статически неопределима и не может быть решена методами статики. Какие-либо данные для раскрытия статической неопределимости методами сопротивления материалов отсутствуют. Поэтому единственный выход—упростить расчетную схему, приведя ее к статически определимой. Один из вариантов такого приведения показан на рис. 4.4, г. Отметим, что к сущест­венным погрешностям в оценке действующих усилий предложенное упрощение расчетной схемы не приведет.

Теперь, пользуясь методами статики, определим неизвестные величины. Анализ представленной на рис. 4.4, а конструктивной схемы показывает, что сформулированная на ее основе задача относится к классу задач на равновесие системы тел. В системе может быть выделено три самостоятельных тела: бурильные трубы, блок и буровой станок. Поскольку взаимное расположение этих тел строго не зафиксировано, решение задачи целесообразно осуществить, рассматривая равновесие каждого тела в отдельности.

В качестве первого тела выделим бурильные трубы. Схема действующих на них сил и система координат показана на рис. 4.4, 6.

Среди заданных величин можно выделить силу тяжести Q буриль­ных труб, подъемную гидравлическую силу Fr, в качестве неизвест­ных— нормальную реакцию N стенок скважины, силу трения frр и натяжение Т каната. Таким образом, в системе сил, которые можно считать сходящимися (силу трения FTp условно можно перенести в точку О параллельно, а появляющейся при этом парой сил пренебречь), имеется три неизвестных величины, тогда как для плоской системы сходящихся сил можно составить только два уравнения статики. Но в данном случае рассматривается предельное состояние, для которого Frp = Nf, следовательно, остается две неиз­вестные величины и задача становится статически определимой:

!Fta = 0, —(Q— FT) cos в— Frv + T= 0; (4.34)

0, A-(e-Fr)sin6=0. (4.35)

Из (4.35) найдем

N=(Q-Fr)sin6. (4.36)

Ho Q = Hq, a Fr=Hqytly, тогда

N=Hq( 1 —Yi/y)sin0. (4.37)

Сила трения определится как

F, г = ‘i f= ‘i’i f ■ ■ — Yi /y)sin 0. (4.38)

Воспользовавщись равенством (4.34), найдем

T=Hq\ — Y,/y)(cose+/sin 6). (4.39)

Предположим #=500 м, </ = 60 Н/м, yl = 12000 Н/м3,

у = 78000 H/m3, 0=30%/= 0,4, тогда Г«27000 Н.

86

Рассмотрим теперь равновесие блока (рис. 4.4, в). Легко опре­делить, что FB = 2 Т. Для условий, приведенных выше, FB — 54 ООО Н.

Наконец, рассмотрим в качестве объекта равновесия буровой станок (см. рис. 4.4, г):

= 0. AVt-7’nSin0=0;

7’лсо80+Ув-Р+У£ = О,

2>d(^)="= — Ра+ГЕЫ 0.

Из (4.40) находим

XD= — Тд sin 0. (4.43)

Из формулы (4.42) определяем

YE = Pall. (4.44)

‘Из формулы (4.41) находим

YD=P-Tcosd-Pall. (4.45)

Предположим, что Р= 14000 Н, а=0,6 м и Ъ= 1,5 м. Тогда *д=-13 500Н, У£= 5600 Н и Yd= — 14983 Н. Знак минус при вели­чинах сил Хв и Yd показывает, что эти силы направлены не как показано на рис. 4.4, г, а в противоположные стороны.

Определять полную реакцию опоры станка в точке D не обязательно. Предполагая симметричное расположение станка от­носительно вертикальной плоскости, болт в опоре D следует рас­считывать на разрывное (растягивающее) усилие от половины силы Уд и срезающее усилие от половины силы Хв (станок к основанию крепят четырьмя болтами). В реальных условиях на такие силы болты не рассчитывают, так как эти силы будут намного больше (учитываются коэффициенты прихвата инструмента либо расчет ведется на максимальную грузоподъемную силу лебедки при «опро­кидыванию» приводного электродвигателя).

Комментарии запрещены.