Бурение грунтовых зондов, установка энергетических колодцев

Из практики бурения скважин и шурфов вращательным способом в рыхлых и мягких порода# известно, что при встрече породораз­рушающего резца с валуном или крупной галькой крутящий момент на валу привода бура резко возрастает. Рассмотрим механику этого процесса.

На рис. 11.1 показана упрощенная модель явления. Прямоугольный резец шириной b перемещается с очень малой скоростью в горизон­тальном направлении, срезая стружку грунта высотой At. Вертикаль­ному перемещению резца вверх препятствует шероховатая поверхность А, имитирующая устройство передачи буру осевой нагрузки. Естест­венно, такая передача осуществляется вращателем бурового станка или иным устройством (например, просто весом инструмента) на по — 206

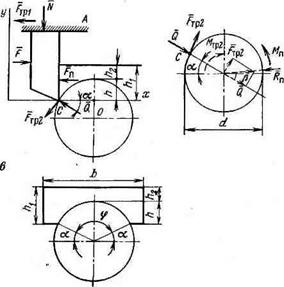
Рис. 11.1. Схема сил, действующих на резец (я), валун (б) и проекция на вертикальную плоскость срезаемой грунтовой стружки (в)

верхности, а не в скважине. Однако для модели это принципиального — значения не имеет. Чем больше передаваемая осевая нагрузка, тем больше будет затрачено энергии на преодоление возникающих во вращателе сопротивлений (имеются в виду сопротивления именно и только во вращателе, моделируемые силой FTpl). Предполагая, что резец перемешается с малой скоростью, можно рассматривать задачу, как статическую.

В некоторый момент времени резец в точке С встречает валун или крупную гальку, которая для упрощения моделируется шаром диаметром d. Также для упрощения будем считать, что валун располагается в створе движения резца, т. е. размеры валуна мало выходят за пределы створа либо совсем не выходят, ограниченные шириной резца. Расстояние от верхней кромки валуна до поверхности срезаемой стружки грунта обозначим буквой Л2, высоту выступающей части валуна Л. Требуется определить. силу F.

Силы, действующие в момент встречи резца с валуном, показаны на рис. 11.1. На резец действуют (рис. 11.1, о): F—активная горизон­тальная сила, обеспечивающая движение резца; N—нормальная реакция шероховатой поверхности; FTpl — сила трения шероховатой поверхности; Fn—сила сопротивления срезаемой стружки грунта; Q—нормальная реакция валуна; Ттр2^сила трения резца о валун. На валун действуют (рис. 11.1,6): к..—нормальная реакция грунта,

направленная в сторону, противоположную действующим на валун активным силам (под углом (3 к линии действия силы Q); Q — нормальная сила, действующая со стороны резца на валун; М„— момент трения породы о валун. Этот момент, очевидно, будет уравновешивать активный момент Мтр2, создаваемый силой Етр2. Силой тяжести валуна и вертикальной силой трения передней грани резца о породу пренебрегаем.

Зная сопротивление породы, т. е. силы R„ и F… коэффициенты трения резца о шероховатую поверхность /1 и о валун /2, а также диаметр валуна d и высоту его выступающей части Л, определим силу F, пользуясь условиями равновесия статики—0, £F*y=0, Y, mo(Fk) = 0. Для этого введем вспомогательный угол а, составленный вектором силы Q с горизонталью, Направление осей л- и у показано на рис. 11.1, а.

После составления исходных уравнений равновесия и преобразова­ний окончательно получим

+

+-?£L=t{d-Щ (/1+/2)+2y/h(d— Л)(1—/i/г)], (11.1)

где от—сопротивление породы разрушению, Н м-2.

Если ширина резца существенно больше диаметра валуна d, то нормальная площадь сегмента, образованного выступающей частью валуна S2, может приниматься равной нулю, и тогда формула (11.1) упрощается. .

. Выражение (11.1) однозначно определяет значение силы Е в за — — висимости от входящих в него параметров. Для случая, когда угол а мал (резец встречает валун почти в экваториальной плоскости), сила FTР2 не будет предельной. Для этого случая N практически обращается в нуль и, следовательно, Етр2 = 0. Тогда

F?<T(d2+2lul-4h2). (11.2)

Из зависимостей (11.1) и (11.2) следует, что встреча резца даже с небольшим валуном приводит к резкому повышению сопротивления породы. Так, при диаметре валуна 0,08 м, cr=4-106 Н м-2, /, =0,2 и /2 = 0,5 сопротивление породы возрастает почти в 10 раз.

Экспериментальные исследования, проведенные на лабораторной установке МГРИ, полностью подтвердили правомерность представ­ленной модели процесса. В частности, как это следовало из теории, положение точки встречи резца с валуном большого влияния на 208 *

усилие резания не оказывает. Однако четко прослеживается закономер­ность: чем ближе точка встречи с валуном к его верхней кромке, тем больше усилие резания. Минимальное усилие реализуется, когда точка встречи находится в экваториальной плоскости.

С учетом отмеченного на кафедре горного дела МГРИ создан породоразрушающий инструмент, резцы которого сначала как бы «пропускают» валун, а затем, когда резец встретит валун в эк­ваториальной или близкой ей плоскости, «подхватывают» его.

Инструмент выполнен в виде откидного резца (резцов), для приведения которого в рабочее положение используется спиральная пружина. Экспериментальные исследования подтвердили работоспо­собность и целесообразность применения откидных резцов при бурении валунно-галедниковых пород и позволили установить, что они обес­печивают более плавное возрастание нагрузки при встрече с валуном, чем жесткое закрепление. Усилие при встрече подпружиненного породоразрушающего органа с валуном в 6 раз ниже, чем при диалогичных условиях, но с жесткозакрепленными резцами. Много­кратное воздействие подпружиненного породоразрушающего органа на валун приводит к последующему снижению усилий на перемещение валуна, поскольку каждое очередное воздействие обусловливает уве­личение обнажения валуна и уменьшение плошади контакта его с породой.

Угол, при котором резец начнет «выворачивать» валун с забоя (после освобождения его верхней части от породы)

a=arctg/2. (11.3)

А

Если tga выразить через линейные величины /г3 и d, где /г?=- — /г (см. рис. 11.1), то

d (1 i/1)1’2

2Лз /г

При /2 = 0,5 это отношение равно 2,24. Иными словами, валун начнет «выворачиваться» с забоя, если его верхняя часть обнажится на h = 0,md или более. Чем больше коэффициент трения между резцом и валуном, тем эта предельная величина меньше.

Выше был рассмотрен процесс срезания стружки рыхлой породы, в которой содержится валун, исходя из предположения, что резец перемещается с очень малой скоростью. Однако скорость соударения резца и валуна мбжет быть и значительной, поэтому возникновение динамической (ударной) реакции валуна неизбежно. Но при самых неблагоприятных условиях динамическая составляющая мощности при соударении резца и валуна составляет не более 10% обших затрат мощности на забое. Ударные усилия незначительны и в при­ближенных расчетах их можно не учитывать.

в породе при встрече им одного валуна:

(11*5)

(11.6)

11.3. РАСЧЕТ ДОПОЛНИТЕЛЬНОГО УСИЛИЯ ПРИ ВНЕДРЕНИИ < КОНУСНОГО ИНСТРУМЕНТА В ПОРОДУ, СОДЕРЖАЩУЮ ВАЛУНЫ

Задача формулируется следующим образом. При. вдавливании в мягкую породу с очень малой скоростью конуса с диаметром! основания D и углом при вершине а в некоторый момент времен^ конус своей боковой поверхностью наталкивается на валун шарооб­разной формы диаметром d. Требуется определить, на какую величину возрастет усилие вдавливания Р. Как видим, задача ставится примерно так же, как и в предыдущем разделе.

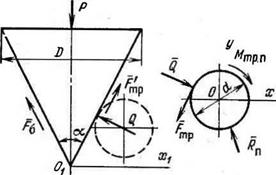
Силы, действующие в момент встречи конуса с валуном, показаны на рис. 11.2. На конус действуют (рис. 11.2, я): Р—активная вер­тикальная сила вдавливания, обеспечивающая движение конуса; Q-. нормальная реакция со стороны валуна; F’rр—сила трения между валуном и конусом; Ре—сопротивление грунта по поверхности конуса. На валун действуют (рис. 11.2,6): Q — нормальная сила со стороны конуса на валун и FTp—сила трения конуса о валун. Эти две силы для валуна являются активными. Со стороны грунта на валун действуют R„ — нормальная реакция породы, направленная в сторону, противоположную действующим на валун активным силам, и Л/1р. „— момент трения породы о валун. Этот момент, как и. в предыдущем случае, очевидно будет уравновешивать активный момент, создава­емый силой Fr р — Весом валуна пренебрегаем.

Зная сопротивление породы, т. е. силы F6 и, к„, кэффициент’ трения / конуса о валун и диаметр валуна с/, можно определить силу, обеспечивающую вертикальное движение конусного наконечника

Два последних слагаемых в формуле (11.5) и представляют собой дополнительную силу, необходимую для преодоления усилий, которые) возникают при перемещении валуна: {

nd2a.

Величина дополнительного усилия в первом приближении будет пропорциональная числу валунов, одновременно находящихся в кон­такте с конусом.

Если порода представляет собой сплошные валуны, промежутки между которыми заполнены, например, суглинком или любой другой рыхлой породой, то максимальное число валунов, одновременно контактирующих с конусом, можно определить (из геометрических соотношений) по приближенной формуле

^яоя~4(1 4-/ 2U/2 (sin al2+-f cos а/2).

n{D+d)D

4d2 sin а/2 ’

а

Рис. 11.2. Схема сил, действующих на конус (а) и валун (б)

Формула (11.7) тем точнее, чем больше диаметр основания конуса и чем меньше диаметр валунов. Тогда максимальное дополнительное усилие можно определить по формуле

(11.8)

(ЛспЦх-16(} lf2yl! sina/2 (smа/2 +/cosа/2).

(11.9)

Если известно ориентировочное содержание валунов в грунте по объему С, то число валунов, одновременно находящихся в контакте с конусом, может быть определено по формуле

П Лтах Е*.

Расчеты, проведенные по формуле (11.8) с учетом (11.9) при о=4 • 106 Н м"2. <7=0,01 =0,25 м, /=0,1 1 и а=0—180°, показывают,

что дополнительное усилие существенно зависит от диаметра валуна ■ d ив незначительной степени — от угла конуса а. Анализ формул позволяет сделать следующие выводы. При увеличении диаметра валуна до 0,2 м дополнительное усилие, необходимое для внедрения конуса, возрастает в 4 раза. Дополнительное усилие в среднем пропорционально содержанию валунов в грунте. При разработке конусных породоразрушающих инструментов необходимо иметь в виду, что угол конуса должен находиться в пределах 30—60" и не превышать 90°. В противном случае дополнительное усилие может возрасти.

Комментарии запрещены.