Бурение грунтовых зондов, установка энергетических колодцев

В разделе 4.4 был определен момент, необходимый для вращения обсадных труб. Если этот момент разделить на наружный радиус R=Dj2, можно получить суммарную силу трения, действующую по наружной поверхности обсадных труб:

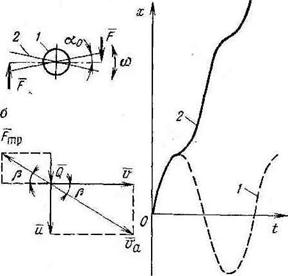
Рис. 5.10. Расчетная схема процесса погружения обсадных груб в скважину ‘ методом расхаживания: . а — труба в плане: / ipyCa: 2 — рычаги для расхаживания груб: о схема скоростей. ючки на поверхности фубы и явствующих на ючку сил; в — график движения груб J в скважине

Принципиальная расчетная схема процесса погружения обсадных труб в скважину приведена на рис. 5.10. При погружении труб в скважину методом расхаживания им сообщается вращательное движение с меняющейся по закону синуса или косинуса угловой скоростью (рис. 5.10. а).

Если мысленно представить всю поверхность обсадных труб в виде точки, то F, p будет направлена в сторону, противоположную абсолютной скорости v0 точки на поверхности трубы (рис. 5.10,6). Эта абсолютная скорость складывается из двух составляющих: горизонтальной г, т. е. относительной скорости, и вертикальной и (скорости движения труб вниз), т. е. переносной скорости.

В задаче дано: частота колебаний труб /г, угловая амплитуда колебаний а0, вес 1 м труб г/, длина труб Н, сила трения, действующая по поверхности труб, Frf). Необходимо определить среднюю скорость погружения труб в единицу времени.

При заданной частоте колебаний труб п (кол/с) период (с) колебаний определится выражением

Если исходить из того, что колебания труб совершаются по

угловая частота колебаний (с-1)—

гармоническому закону, то угол а отклонения труб в данный момент

времени / по отношению к среднему промежуточному положению

определится по формуле

a = aosiniM = aosin27t/H, (5.70)

а угловая скорость

(0 — a = da/dt = 2Tzna0cos2niH. (5.71)

тогда

v=(aR=(oD/2 — KDnoi0cos2Knt. (5.72)

Мгновенная вертикальная скорость движения труб вниз Q

t/ = 7r/)ffa0,-Fj— —2 ‘ 42 cos 2л:/)^ (5-73)

— Гр тр)

где

e/(F? P-eT2P),/2 = tgp (5.74)

(см. рис. 5.10, б): Q—вес труб (или, что то же — осевая нагрузка).

В первом приближении

Q=qH. (5.75)

Обозначим выражение nuna^Oi у — L—буквой А, так как все

величины, входящие в него, не зависят от с, тогда получим

u — Acos2jtnt. (5.76)

Мгновенную скорость и можно представить как производную от

перемещения колонны вниз по времени

u = dx/dt. (5.77)

Разделяя переменные и интегрируя, получим

A cos 2nntdt — A — Ш—П— + Ci, (5.78)

2itn

где — постоянная интегрирования.

При г = 0 имеем х = 0, следовательно, С, =0, и закон движения

труб запишется в виде -•

А

х—-—sin27r/H. (5.79)

[ 2тш ж ‘

Графически эта зависимость представлена кривой / (рис. 5.10, в).

I Но так как перемещение колонны может происходить только в одном

г

направлении (вниз), т. е. х может быть только положительным, то J график примет вид кривой 2.

Отсюда пройденный колонной за период Т путь х* равен ■ амплитудному значению координаты х, умноженному на 4, т. е.

х’ = 2А/кп. (5.80) ■

Подставляя в формулу (5.80) значение А, получим

x — = Da0Q/Flo-QiD)^. (5.81)

Средняя за период скорость погружения колонны определится как

и’=х’п. (5.82)

После подстановки (5.75) и (5.81) с учетом (5.67) и (4.29) в (5.82) для песчаных пород получим

. . ADooqn

и = _ . , (5.83).

v/j>^Y./mg1(45"-<P/2j]i~4?‘

где ф — угол внутреннего трения песка; у— объемный вес грунта, Н/м3, Рассчитаем время погружения колонны труб заданной длины в сыпучий грунт. Мгновенная скорость погружения труб может быть представлена в виде

u=dH/dt. (5.84)

Тогда

(5.85)

dt = —,dH, и

или

dt—

%/[лР/у/У1д2(45° —ф/2)]2 —4</2

(5.86)

4DoL0qn

Взяв от выражения (5.86) определенный интеграл, получим

J <5’87)

nZ)/Ytg2(45° —ф/2)

11 =

и h, —

(5.88)

tiD/y tg2(45r—ф/2) получим н ________ h—bi \jH2 — adH. о

4DvLoqn Обозначив 2 q

7rP/ytg2(45° nfy tg^(45j-»p/2) 4qa0n

Формула (5.90) ^действительна только для несвязных сыпучих грунтов, угол внутреннего трения которых превышает 10′ и лобовое сопротивление незначительно. При малых углах ср формула приоб­ретает более простой вид в связи с тем, что tg2 (45" — ср/2) можно принять равным единице:

(5.91)

у/(яР/уЯ)2~4<7-у| V" ’ nDfy

Формулой (5.91) удобно пользоваться при предварительных*ори­ентировочных расчетах.

Для связных глинистых грунтов следует иметь в виду, что FTр определяется на основании формулы (4.30). Для этих грунтов средняя скорость погружения труб может быть рассчитана по формуле

(5.92)

и*=2Da0nHq j (F2P — Н 2 q2)112.

Вычисление времени погружения труб в этом случае представляет некоторые трудности, поскольку получающийся интеграл к табличному виду не приводится и должен вычисляться с помощью ЭВМ.

При использовании метода расхаживания трубам, как правило, не сообщают возвратно-вращательного движения в связи с тем, что при этом может произойти развинчивание труб в резьбовых соедине­ниях. Существующие механизмы расхаживания позволяют сообщать трубам прерывно-вращательное движение только в одну сторону.

В этом случае средняя скорость погружения, определяемая выраже­ниями (5.83) и (5.92), должна быть уменьшена в 2 раза, а время погружения [см. (5.90) и (5.91)] увеличено в 2 раза.

?7T Dll v’L“"./ Г" 1ё Н-* Ч;/

Рассмотренная выше методика расчета скорости и времени погружения труб с успехом может быть использована при вращении труб. При заданной частоте вращения труб и„ (об/с) скорость погружения труб в сыпучий грунт определяется выражением

(5.93)

Время погружения труб можно вычислять с помощью выражения

(5.91) с тем, однако, условием, что коэффициент, стоящий перед квадратными скобками, будет иметь вид 1 jnDnB.

При значительном лобовом сопротивлении в формулу (5.67) следует подставить значение Мтр, вычисленное по формуле (4.31).

Анализируя рассмотренную выше задачу, легко прийти к выводу, что наиболее существенным элементом в ней, позволившим получить искомый результат, являлось представление движения точки на поверхности трубы, как участвующей в двух движениях: переносном (поступательное движение трубы вниз) и относительном (движение точки по окружности). Не менее важным элементом следует считать также представление о движении трубы, как статическом процессе. Все представленные соотношения справедливы только при малых угловых частотах вращения и малых скоростях погружения трубы. При значительных скоростях (п> 1 кол с-1 и м*> 0,001 м — с ~’) задача становится существенно динамической и должна решаться соответствующими методами. Рассмотренное решение в этом смысле следует считать приближенным.

При закреплении стенок скважины обсадными трубами с муф­товыми соединениями в приводимые формулы необходимо вводить поправочный коэффициент, ориентировочное значение которого со­ставляет 1,1 —1,5. Скорость погружения должна уменьшаться в указан­ное число раз, а время погружения соответственно увеличиваться. Чем в более плотные грунты погружаются трубы, тем меньше значение коэффициента следует принимать.

Пример. Подсчитаем значение средней скорости погружения труб для реального случая при следующих исходных данных: ао=0,218 рад, £>=0,219 м, трубы ниппельного соединения, и = I кол • с _ 1, ф = 28 . q = 366 Им1, /’=0.3, 7 = 20000 Н м 3 и //=50 м. ^

По формуле (5.94) получим /Г = 9,385 ■ 10 4м-с-1. С такой средней скоростью будет погружаться колонна труб, заглубленная в грунт на 50 м.

Задача, рассмотренная в настоящем разделе, решается на основе чисто кинематических соотношений. Однако эта задача по существу динамическая. Выводы, полученные с учетом кинематических пред­ставлений, справедливы только в том случае, если возникающие

ускорения намного меньше ускорения свободного падения g.

«

Комментарии запрещены.