СВЯЗИ И СИЛЫ РЕАКЦИЙ СВЯЗЕЙ
СВЯЗИ И СИЛЫ РЕАКЦИЙ СВЯЗЕЙ
Тело, перемешениям которого в пространстве препятствуют какие; нибудь другие скрепленные или соприкасающиеся с ним тела, называется несвободным. Все, что ограничивает перемещения Данного ‘ тела в пространстве, будем называть связью.
Тело, стремясь под действием приложенных активных сил пере’ меститься, чему препятствует связь, будет действовать на нее с некоторой силой, называемой силой давления на связь. Одновремен — :■ но по четвертой аксиоме связь будет действовать на тело с такой t — же по модулю, но противоположно направленной силой. Сила, с которой данная связь действует на тело, препятствуя тем или ■ иным его перемещениям, называется силой реакции (противодействия) связи, или просто реакцией связи. Здесь необходимо особо подчеркнуть | существенное различие между активными силами и реакциями связей. Модуль и направление активных сил непосредственно не зависят от других действующих на тело сил. Направление и величина реакций связи всегда зависят от активных сил. Более того, они зависят
| также от других реакций связей. Подавляющее большинство задач
; статики, в том числе в бурении, сводится к определению величины и направления реакций связей, возникающих при действии на
исследуемые конструкции активных сил. Примерами активных сил
! являются сила тяжести, усилия, развиваемые лебедкой бурового
станка (при рассмотрении равновесия вышки или мачты), усилие на
крюке и другие силы; реакции связи—усилия в местах крепления мачты к раме, действующие на опорные домкраты усилия, и т. д.
При определении направления реакции связи следует руководствоваться следующим правилом: реакция связи направлена в сторону, противоположную той, куда связь не дает перемещаться телу. В задачах статики обычно определяют модуль и направление реакций связей. Для некоторых видов связей направление реакций может ; быть определено сразу, в других случаях связь одновременно препятствует перемещениям тела по нескольким направлениям; тогда направление реакции связи также наперед неизвестно и должно определяться в результате решения рассматриваемой задачи.
Рассмотрим направления реакций некоторых основных видов связей. Реакция гладкой поверхности или опоры направлена по общей нормали к поверхностям соприкасающихся тел в точке их касания и приложена в этой точке. Когда одна из соприкасающихся поверхностей—точка, то реакция направлена по нормали к другой 5 3477 65
поверхности. Реакция гибкой нерастяжимой нити (каната, цепи и т. д.) направлена вдоль нити к точке ее подвеса. Реакция ненагруженного стержня (кроме его шарнирных опор), весом которого можно пренебречь, направлена вдоль оси стержня. Реакция цилиндрического шарнира может иметь любое направление в плоскости,’ перпендикулярной к оси шарнира. Обычно такую реакцию раскладывают по двум перпендикулярным осям и определяют каждую составляющую. Таким образом, реакция плоского шарнира содержит в себе заранее две неизвестные величины. Реакпия шарового шарнира или подпятника может иметь любое направление в пространстве. Эту
|
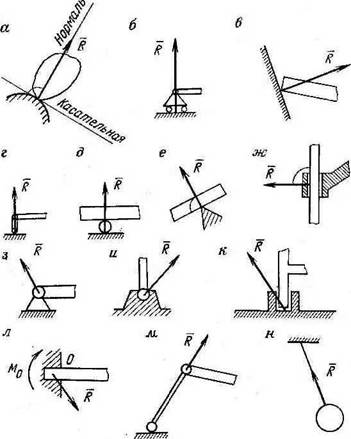
Рис. 3.1. Наиболее распространенные типы идеальных связей: а, в, е —точечная опора; 6, г, д—подвижная шарнирная заделка; ж, з—плоский шарнир; м—шаровая пята; к—подпятник; л—неподвижная шарнирная заделка; м~ невесомый стержень; и—нерастяжимая нить |
реакцию раскладывают уже по трем взаимно перпендикулярным осям и, следовательно, она содержит в себе три неизвестные величины. На рис. 3.1 представлены наиболее распространенные типы идеальных (без трения) связей. Все они в итоге могут быть сведены к шарнирной опоре и жесткой заделке. Для плоских задач реакция подвижной шарнирной опоры направлена по нормали к поверхности, на которую опирается подвижная опора; неподвижная шарнирная опора соответствует плоскому или шаровому шарниру. Наконец, в жесткой заделке при плоских задачах, помимо двух составляющих реакций заделки (по двум взаимно перпендикулярным осям), возникает пара с неизвестным моментом (жесткая заделка препятствует повороту такого тела). В пространственных задачах полная жесткая заделка содержит в себе шесть неизвестных величин: три составляющие реакции заделки и три пары, дёйствующие в трех плоскостях, перпендикулярных к выбранным трем взаимно перпендикулярным осям.
В заключение отметим, что равновесие несвободных тел в статике (как и движение тел в динамике) изучается на основании следующей аксиомы связей: всякое несвободное тело можно рассматривать как свободное, если отбросить связи и заменить их действие реакциями этих связей.