Бурение грунтовых зондов, установка энергетических колодцев

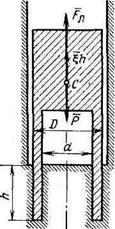
При «клюющем» способе бурения ударная штанга вместе с по-J родоразрушающим инструментом в виде трубы, оборудованной j башмаком, сбрасывается с некоторой высоты на забой скважины, j в результате чего приобретает запас кинетической энергии, которая! расходуется на преодоление сопротивления породы в процессе внедре — 1 ния инструмента. Снаряд после каждого удара извлекается на j поверхность для его очистки от грунта. Схема действия сил на J инструмент, внедряющийся в грунт при чистопластическом характере 3 разрушения последнего, показана на рис. 7.5. Сопротивления породы складываются из сопротивлений по лобовой и боковой поверхностям ‘ кольцевого инструмента. Первые являются постоянными, вторые— i зависят от перемещения h (текущее перемещение инструмента в по — ) роде). Ставится задача: определить величину hmax погружения инст — ’ румента в породу за удар.

Сделаем ряд допущений: 1) породоразрушающий инструмент пред — ’ ставляет собой гладкую трубу с плоским торцом и является абсолютно твердым телом; 2) сопротивления, пропорциональные скорости движе — • ния инструмента, отсутствуют; 3) упругие деформации породы от­сутствуют.

Поскольку действующие на снаряд силы постоянны (вес Р, лобовое сопротивление FtI) или зависят только от перемещения (боковое сопротивление Fr.=chi. а снаряд движется поступательно, для определения величины внедрения инструмента за удар вос­пользуемся теоремой об изменении кинетической энергии точки в интегральном виде—выражением (6.54).

В конце погружения снаряд остановится, следовательно v, = 0.

В момент соприкосновения снаряда с породой его скорость равна Г(1 и может быть определена в соответствии с рекомендациями трех предыдущих разделов.

Сумма работ будет складываться из составляющих;

и

Ai = Ph~.„. А2= ~Frh~.r. А3= jF6dh;

о

F6=fyi = n(D+d)hf-

Рис. 7.5. Схема действия сил на инструмент, внедряющийся в породу при «клюющем» буре­нии при чистопластичсской модели грунта:

? = 7t(/J + f/)/

SHAPE * MERGEFORMAT

(7.30)

Подставляя полученные значения в (6.54) и проведя преобразова­ния, определим

(7.31)

В формуле (7.31) Fl-(D’-Ji)nR/4,

где удельное сопротивление породы по лобовой поверхности (ориентировочно может приниматься по табл. 2.40).

Теперь определим ту же величину погружения за удар при упругопластической модели грунта. Такая модель представляет собой среду, при внедрении в которую инструмента первоначально пре­одолеваются упругие сопротивления, а затем по достижении на торце инструмента усилия, равного постоянному сопротивлению горной породы, пластические сопротивления. Эта модель более близка к реальным глинистым грунтам. Она дает возможность учесть случай, когда процесс погружения инструмента не происходит, а вся накопленная энергия тратится только на упругие деформации горной породы.

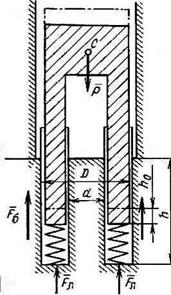
Схема «клюющего» бурения при упругопластической модели показана на рис. 7.6. Для упрощения будем задаваться не коэффициентом жесткости грунта, а величиной h0 упругой деформации горной породы. Поскольку в рассматриваемой модели все

Рис. 7.6. Схема «клюющего» бурения при упругопластической модели горной по­роды

действующие силы постоянны или зависят от перемещения, для нахождения Лтах, так же как и в предыдущем случае, можно воспользоваться теоремой об изменении кинетической энергии. На основании этой теоремы для рассматриваемого случая легко получить следующее выражение:

(7.33)

В этой формуле обозначения те же, что и в предыдущем разделе. Легко убедиться, что в случае, когда /г0= 0, выражение (7.33) становится аналогичным (7.31).

Из выражения (7.33) можно получить условие, при котором процесс погружения инструмента происходить не будет. Поскольку Fn практически во всех случаях больше Р. то Лшах будет больше нуля только тогда, когда числитель второго слагаемого подкоренного выражения больше нуля (если Р > процесс погружения будет происходить даже если г„ = 0, т. е. при отсутствии начальной скорости инструмента). Следовательно, условие невозможности погружения инструмента будет

mVo^Fnlio-2Pli0.

Приведенные рассуждения справедливы, когда горная порода обладает (хотя бы частично) свойством идеальной упругости, т. е. способностью восстанавливать первоначальное состояние после снятия 166
нагрузки. Однако такой способностью обладают очень немногие разновидности глинистых грунтов. Более того, процесс деформирова­ния грунта таков, что упругие деформации постоянно сопутствуют пластическим, даже при очень малых нагрузках. Поэтому рассмот­ренная выше модель, так же, как и предыдущая, является приближен­ной, а выражение (7.33) может быть использовано для ориентировоч­ных расчетов.

Комментарии запрещены.