Геострофическая модель
Геострофическая модель
Глубина, до которой проникает ветровое течение, называется слоем трения, или экмановскнм слоем трений. Ниже этого слоя движение вод вызывается только градиентом давления. Если по-
ток не имеет ускорений, то в каждой его точке существует равновесие сил, которое можно записать для единичного объема пространства так:
-д£- = йуз2со sin 9, (28)
”fy~ ~ — аха2ш sin <р. (29)
Согласно уравнениям (28) и (29), геострофдческий поток всегда направлен строго перпендикулярно к движущей силе (в северном полушарии вправо от нее, а в южном — влево). Например, если течение вызвано наклоном уровня, то частицы будут двигаться не по уклог ну, а перпендикулярно к нему. Название «геострофиче — ская модель» показывает, что движение целиком контролируется поворотным ускорением Земли. Модель предполагает, что вода лишена инерции, если не считать силы Кориолиса, поэтому петли, показанные на рис. 2 а, в геострофическом течении Не возникают. Безынерцион — ность воды противоречит ее ф, изической природе. Например, лишенная инерции вода, вылетая из бранд — сбойта, должна была бы падать вертикально вниз. Поэтому уравнения (28)—(29) принято называть геостро — фическим приближением. В связи с тем, что скорости морских течений изменяются от точки к точке очень постепенно, величина членов уравнения, выражающих силы инерции, невелика. Напомним вид этих членов:
ах + «у * — инерционные ускорения по оси*, диу диу
Ux~~dx ^ иУ~~ду инерционные ускорения по оси у.
Измерения показывают, что в большинстве районов океана геострофическое приближение оправдано и оно служит основным способом расчета течений, вызванных градиентами давления, иными словами —градиентных течений.
Все течения океана можно разделить в соответствии с вызывающими их силами на ветровые, градиентные и приливные. В реальных условиях эти виды течений могут существовать в одной и той же точке одновременно.
Две теоремы о течениях и их применение к Гояьфстриму ‘
В тексте этой главы мы пока редко встречаем отечественные имена, хотя нашими учеными созданы важные и принципиально новые модели крупномасштабных океанических процессов. Первыми из них были модели: взаимодействия океана, суши и атмосферы
В. В. Шулейкина;‘ взаимодействия океана и льдов — Н. Н. Зубова; воздействия атмосферы на океан — В. Б. Штокмана. Мы обратимся к некоторым из последних отечественных моделей, но раньше расскажем о двух открытиях норвежского геофизика X. Свердрупа, полученных самым простым математическим путем и оказавшим значительное влияние на дальнейшие пути океанологической мысли. Изложим эти открытия в виде двух теорем.
. Теорема 1. Между изменением вертикальных размеров элементарных объемов воды геострофического течения и направлением движения этих объемов существует такая связь, что объемы, движущиеся к полюсу, растягиваются по вертикали, а движущиеся к экватору— сжимаются.
Важным следствием этой теоремы будет то, что ‘Меридиональные движения в океане многослойны. Действительно, если — поток занимает вею толщу океана от поверхности до дна, то он не может двигаться к полюсу, так как, растягиваясь по вертикали, будет повышать уровень моря в направлении своего движения. ‘
Наблюдения: показывают, что и в Арктике, и в Антарктике смещения океанических вод в направлении экватор—полюс имеют многослойный характер. Слабое противотечение обнаружено также под Гольфстримом у берегов Америки и в других меридионально направленных океанических потоках.
Теорема доказывается аналитически. Направим ось х на восток и ось у на север. Перепишем уравнения гео — строфического движения: . ■ •. ■
-г-яг=“А <3°)
• 1 др
а ду
где fi = 2cosintp — планетарный вихрь 50
‘ Перекрестно продифференцируем уравнения:
1 &р _ . р диу n9V
а дхду У ду ду ’ ‘ ‘
В правой части уравнения (33) стоит только один член, так как величина Q не изменяется по оси х. Вычтем уравнение (33) из уравнения (32):
‘ даг, дау иу
дх ‘ ду й ду "
Вспомним теперь уравнение неразрывности из раздела «Математические модели течений». Это уравнение имеет вид
Приравнивая друг к другу (34) и (35), получим
“>=a(-f/ <36>
где множитель М — величина безусловно положительная.
Таким образом, теорема доказана для случая, когда плотность воды 0 не изменяется по осям х и у. Уравнение (36) выражает связь между двумя величинами: скоростью вдоль меридиана (иу) и вертикальным растяже* нием (dujdz) элементарного объема воды в потоке. Если правая часть уравнения положительна, то объем растягивается по вертикали, но тогда положительной оказывается и левая часть уравнения, а это означает, что меридиональная скорость течения направлена к полюсу. Если правая часть уравнения отрицательна, то объем сжимается по вертикали и его движение направлено к экватору. Эта связь широко используется для вычислений вертикального движения воды.
На рис. 10 показана схема трехслойного течения в океане в произвольно взятой точке. Попытайтесь продолжить границы между потоками, учитывая, что движение стационарно. Вы столкнетесь с физическим
противоречием. Возможно, вы найдете ему объяснение или обнаружите противоречия в выводе теоремы. Вывод этот сделан формальным путем, но у него существует и физическое толкование.
|
Поверхность ♦ 6= ‘♦ S. |
|
*<=> * TTrfrrr Дно |
При вращении Земли вокруг своей оси произвольный объем, вырезанный из тела планеты, в том числе из ее атмосферы или океана, совершает сложное движение. Из физики нам известно, что любое движение может быть представлено как результат совмещения двух элементарных движений: поступательного, при котором любая линия, мысленно проведенная внутри тела и связанная с его частицами, перемещается параллельно самой себе, и вращательного вокруг некоторой оси. Если спроектировать вектор вращательного движения на перпендикуляр к площадке, касательной к поверхности Земли, получится: cosincp= = Ч2 Q. Это значение равно угловой скорости, с которой элементарный объем вращается вокруг оси, проходящей через него и направленной к центру Земли. При этом объем остается неподвижным относительно земных ориентиров, хотя и об — rm.. ■ і — ладает реальным моментом количества слойное дви — движения. При изменении формы объе — жение в океане, ма он стремится сохранить свой момент количества движения. Для этого объем, растягиваемый по вертикали, должен увеличить скорость вращательного движения, а объем сплющиваемый — замедлить ее (сравните это с изменением скорости вращения конькобежца-фигуриста, то раскидывающего, то соединяющего свои руки). .
Объем, изменивший скорость вращения, приходит в противоречие со скоростью вращения подстилающей поверхности Земли, и это вызывает его движение относительно земных ориентиров. Он может начать видимое земному наблюдателю вращение или сместиться вдоль меридиана — на ту широту, где его новая скорость вращения будет соответствовать планетарному вихрю и таким образом станет невидимой для земного наблюдателя. Оказывается, что выполнить второе условие легче, хотя физические причины этого оставляют место для размышлений. ,
Океанологами они пока не разъяснены, и хочется призвать читателя подумать над этим. — .
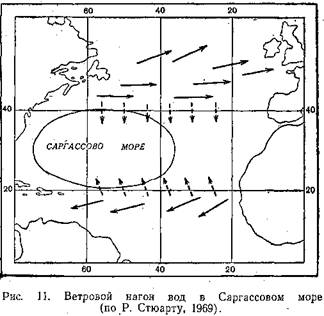
Во всяком случае, если сжатие слоя есть не следст — . вие, а причина его движения к экватору, то можно вслед за американским океанографом Р. Стюартом дать дополнительное объяснение схождению вод у экватора. На рис. 11 сплошными стрелками показано направление ветра над Северной Атлантикой, а пунктирными — ветровой перенос воды по модели Экмана (см. выше).Этот
|
Сплошные стрелки показывают ветер, пунктирные — осредненное по глубине ветровое течение. . |
перенос вызывает нагон поверхностных вод в Саргассо — вом море. Нагон ведет к увеличению давления на нижние слои воды, Последние сжимаются по вертикали («расплющиваются»), и это вызывает их движение к экватору.
Теорема 2. Если в произвольно выбранной, но удаленной от берегов точке океана сложить от поверхности до дна скорости смещения по меридиану всех частиц
воды, то окажется, что результирующий перенос воды в направлении меридиана пропорционален пространственной неравномерности ветра, выраженной через вихрь касательного напряжения трения на морской поверхности.
Сделаем пояснение. На рис. § показано распределение касательного напряжения трения ветра в Тихом океане, Все векторы трения направлены по оси х, но они имеют разную длину и поэтому поле трения неравномерно. Вихрем (или ротором) называется характеристика поля в точке, равная в нашем простом примере тангенсу угла наклона линии, соединяющей концы векторов. Этот тангенс берется с обратным знаком и равен производной от хх по у:
|
J^x ду |
|
(37) |
rot,-с,
Если бы векторы трения имели проекции и на ось у, то выражение’ротора было бы
Теперь докажем, теорему. Будем считать, что движение воды вызывается двумя силами: трением ветра и градиентом давления. Трением о дно и берега можно пренебречь. Тогда, если частицы не имеют ускорений (в том числе инерционных ускорений), движение на любой глубине должно отвечать следующим условиям равновесия сил, приложенных к единичному объему воды:
|
|
|
|
|
дг |
|
д |
|
дах |
|
) |
(39)
|
|
|
д |
|
ди |
|
дг |
|
движущая сила трения движу — отклоня» |
|
щая ющая сила сила Кориолиса давле |
(40)
ния
Ось х по-прежнему направлена на восток, ось у — на север, но ось г — вверх.
Введем граничные условия: на глубине £ = 0 движе-
ние затухает и направление трения равно нулю (то=0). На поверхности выполняется ньютонов закон трения:
Проинтегрируем уравнения от глубины z=0 до поверхности z—Н. Удобно направить ось 2 снизу вверх, чтобы избежать знаков минус в формулах (41). В, результате интегрирования в уравнениях появятся полные (суммарные) потоки массы воды, которые мы обозначим через S:
■ я н.
…… sx = J auxdz> sy = I oasdz-
‘ ‘ Zo • *0 ■
Интегрирование градиентной силы нужно проводить с учетом того, что под знаком интеграла происходит дифференцирование. Например, в уравнении (39) мы получим ".
[ — ж — dz= -k-[pdz — — ъгр*+-ъгр*-‘
Zq *0.
Если давление на поверхности моря (рн) равно нулю и глубина нулевых скоростей или дно океана (z0) горизонтально, то два последних члена в правой части записанного равенства обратятся в нули. При этом, обозначив буквой Р суммарное давление воды, получим
. Zq Zq
Н Л А И
J •—/ ->dz = —д—J pdz = — I дУ дУ і ‘
Теперь можно переписать результаты интегрирований (39) — (40) по глубине моря следующим образом:
дР QSy, (42)
дх У
|
&SX, (43) |
дР
і
у ду
где хх, ху— составляющие трения ветра по осям х и у.
Перекрестно продифференцируем уравнения (42) и (43): ■
^ (44)
. ду дхду ду у ду
‘ д2р _п dftr (ДЪ
дх дхду ~ дх * ^Ь>
Эта операция позволяет теперь исключить из уравнений давление Р. Для этого вычтем одно уравнение из
другого:
dzy ді, п / dSr, dSy , о
дх ду
Если уровень моря г = Н и горизонт нулевых скоростей z=z0 не изменяются во времени, то физическое условие неразрывности всего столба жидкости выразится так: .
|
dSx ■ 9S, дх ‘ ду |
|
у |
■ 0» (47)
Учитывая выражения (47) и (38), перепишем полученный результат (46) в окончательном виде:
" = (-57") 1 rot^- (48)
Таким образом, теорема доказана, но, подчеркнем, лишь для таких мест открытого океана, где можно пренебречь наклоном дна (или наклоном границы нулевых скоростей, когда таковая имеется) . —
Равенство (48) означает, что суммарный (или полный) установившийся поток по меридиану в открытом океане с горизонтальным дном зависит от неравномерности ветра и географической широты места, но совершенно не зависит от поля плотности океанических вод. Этот вывод с физической точки зрения представляется парадоксальным и может послужить’ новой темой для математических размышлений читателя.[9]
Нужно иметь в виду, что уравнение Свердрупа (48) считается одним из самых простых и одновременно плодотворных выводов недавнего прошлого океанологии и используется в десятках серьезных работ. Правда, его физического смысла никто удовлетворительно не разъяснил, и здесь остается лишь провести параллель с известными словами Герца: «Кажется, что эти формулы умнее нас…»[10] .
В уравнении (48) не учитывается трение о дно, однако, если оно по каким-либо причинам существенно, его можно учесть, записав:
|
|
Введенный нами дополнительный ротор должен увеличить суммарный перенос по меридиану. Он входит в уравнение с иным знаком, чем ротор ветра, и имеет иное направление. Ротор ветра направлен по ходу течения, а ротор трения о дно — против хода течения. Таким об-‘ разом, два ротора всегда имеют противоположные собственные знаки. При антициклоническом поле ветра ротор напряжения ветра о воду отрицателен. Противоположно направленный ротор трения о дно будет положительным, и разность двух роторов даст отрицательную величину суммарного переноса. Поскольку положительная ось у направлена к северу, отрицательный перенос соответствует переносу к экватору. В циклоническом движении ротор ветра положителен, а ротор трения о дно отрицателен, их разность даст положительную величину полного потока, т. е. суммарный перенос воды к полюсу. ‘ .
Вторая теорема Свердрупа позволяет показать количественную связь между отдельными звеньями системы. Если мы возьмем среднее по какой-то параллели значение ротора ветра над Атлантикой и умножим его на ширину океана, то по формуле (48) или (49) найдем суммарный перенос вод к экватору. Но если Гольфстрим осуществляет компенсацию этого переноса, то он
Должен иметь соответствующий расход воды. Этот расход был определен американским океанографом В. Манком, для 35° с. ш. по формуле. . .
‘• 1>17 (~1гУ’rot*’[11]‘ (5°)
где L — ширина Атлантического океана, равная на широте 35° с. 6500 км. В этом месте скорость поверхностных вод Гольфстрима равна 100—250 м/с, ширина потока 100 км и его расход 75 млн. м[12]/с.