Бурение грунтовых зондов, установка энергетических колодцев

-. . Рассмотрим теперь океан как управляемую систе­му.1 Такая система состоит из взаимодействующих эле­ментов или звеньев, имеющих определенные функции. На вход системы поступают внешние воздействия, кото­рые управляют переходом системы в новые состояния. Последовательность этих состояний называется поведе­нием, или движением, системы. Кибернетика изучает системы именно с точки зрения их Поведения под влия­нием управляющих воздействий. Поэтому кибернетику •называют теорией управления. Если объект управления :и устройство, подающее управляющие воздействия, рас­сматриваются совместно, они объединяются под назва­нием системы автоматического управления. В этом слу — ,чае управление осуществляется самой системой, напри­мер заложенной в ней программой.

Если рассматривать Мировой океан как объект уп­равления, то в его систему управления надо включить Солнце, Луну, атмосферу, земную поверхность и чело­века. Солнце и особенно Луна вызывают приливы, воз­действуя на океан по сложной и строгой программе.

Сверх того, Солнце, тоже по программе, посылает к по­верхности океана лучистую энергию, которая проходит сквозь атмосферу и трансформируется на поверхности океана в тепло. Атмосфера выступает как звено систе­мы управления. На ее вход поступает тепловая энергия поверхности океана, которая преобразуется атмосферой в кинетическую энергию крупномасштабного движения и возвращается на выход в виде механического воздей­ствия атмосферы на океан. / ., ‘ .

Суша воздействует на океан прежде всего через ат­мосферу, создавая у берегов океана контрасты атмо­сферной температуры и давления и вызывая суточную и сезонную смену направлений ветра. Развитие матери­ковых оледенений изменяет уровень и термическое со­стояние океана, а речной сток влияет на химические и биологические процессы. Наконец, с суточным вращени­ем Земли связана отклоняющая сила (Кориолиса).

Перечисленные связи в той или иной мере взаимны даже тогда, когда это не кажется очевидным. Так, не только вращение Земли влияет на течения в океане, но и наоборот, не только Луна влияет на приливы, но й приливы влияют на движение Луны, вызывая ее «веко­вое ускорение». Человек уже при современном уровне техники может оказывать на океан воздействия, доста­точные для изменения течений, температур и площади льдов. .

Звенья системы сами можно рассматривать как ма­лые системы. Для этого они обладают необходимыми признаками: входом звена, принимающим воздействия; оператором звена, преобразующим воздействия; выхо­дом звена. В кибернетике разработана не зависящая от физической природы звеньев их классификация, которая определяет принципиальные характеристики звена — свойства инерции, устойчивость, способность создавать колебания в системе и тому подобное. Характеристики элементарных звеньев могут быть выражены форму­лами.

Для построения модели управления наметим следую­щий путь. Выберем одно из существенных внешних воз­действий на океан — приток солнечной радиации к по­верхности океана. Этот параметр «запрограммирован­ным» образом меняется в. пространстве по поверхности океана и во времени, а также подвержен случайным

колебаниям, связанным, например, с изменением облач­ности. Мы должны проследить, какими путями выбран­ное воздействие управляет поведением системы, на ка­ких участках преобразуется в другие формы сообщений. Это позволит определить те элементы системы, которые существенны для ее функционирования, и выделить звенья элементов, которые обладают внутренним един­ством и выполняют определенную функциональную на­грузку. Каждое звено осуществляет преобразование по­ступающих в него сообщений, что может быть записано так: :

у = Ах, (51)

где х —сообщение, поступающее на вход звена; у— со­общение, поступающее на выход; А — оператор звена, объединяющий все математические и логические дей­ствия над х.

Зная звенья системы и связи между ними, можно со­ставить функциональную схему системы. В схеме отдель­ные звенья обозначаются прямоугольниками, их взаимо­действие — направленными стрелками, а форма переда­ваемых сообщений — индексами. Качественная схема — лишь первая ступень создания модели. Для того чтобы описать механизм управления системой и предсказать ее поведение, нужно найти формальные операторы звеньев. Эти операторы могут быть выражены в виде систем уравнений или матриц преобразований. Новая форма модели будет математической. Дальнейший шаг — ее анализ специальными методами, которыми располагает теория управления и которые позволяют судить о пове­дении системы по характеру и способу соединения ее звеньев.

Итак, проследим один из циклов поведения системы под воздействием солнечной радиации. Сначала примем во внимание лишь пространственное изменение посту­пающей радиации, полагая, что Солнце находится в пло­скости земного экватора. В этом случае изменение при­тока радиации с широтой выразится формулой

‘ — . ■ R (?) = R0 cos?, (52)

где Ro — поступление лучистой энергии на экваторе.

Поток лучистой энергии, проникающий в воду (кото­рая занимает около семи десятых поверхности планеты),

поглощается водой и превращается в тепло по экспонен­циальной зависимости от глубины. В первом сантиметре воды около 30% радиации, а в первом метре около 60% переходит в тепловое движение молекул. Таким обра­зом, тепло генерируется (создается) из лучистой энер­гии у поверхности, откуда оно, с одной стороны, переда­ется в атмосферу и путем турбулентного перемешивания воздуха переносится вверх, а, с другой стороны, путем турбулентного перемешивания воды уходит вниз — в мор­ские глубины. Вертикальный перенос тепла в воде за­труднен тем, что нагревание ее сверху вызывает, как правило, устойчивую стратификацию плотности, а пере­нос в воздухе облегчен тем, что нагревание снизу вызы­вает неустойчивую стратификацию в атмосфере. Нагре­вание приводит к расширению воздуха и пропорцио­нальному удлинению столба атмосферы над океаном. Поскольку нагревание изменяется с географической ши­ротой, то соответственно" изменяется и высота атмо­сферы. .

Мысленно вырезанные в атмосфере вертикальные столбы воздуха мы можем рассматривать как измери­тельные устройства на входе системы управления. Из­менения их длины с некоторым опозданием и искажени­ем регистрируют. величину поступления в. атмосферу тепла, вызванного инсоляцией подстилающей поверх­ности. Если изменение радиации вдоль меридиана обо­значить через AR, а изменение высоты столба атмосфе­ры [13] АН, то соответствие между выходом и входом зве­на можно записать с помощью оператора А\

ДЯ = Л1Д/?. (53)

Изменение высоты атмосферы создает горизонталь­ный градиент давления, направленный вдоль меридиа­на. Пока столбы воздуха, изменяя свою высоту, сохра­няют первоначальную массу, градиент давления возни­кает лишь на большой высоте от поверхности планеты.

Формула (52) справедлива, как уже было отмечено, при условии, что Солнце находится в плоскости эквато­ра. Если приток радиации к разным широтам осреднить
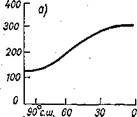
за год, то получим связь, показанную на рис. 12 а. На рис. 12 б показана среднегодовая температура поверх­ности планеты и на рис. 12 в — среднегодовое положе­ние изолинии атмосферного давления (изобара), равно­го 200 миллибаров (1 мбар — давление в 1000 дин на

I см2 поверхности). Эта изолиния проходит на высотах

II — 12 км. Сходные с ней очертания имеют изобары

°С
40
20	—
0	—
-20
-40

6}

JL

кш/см

км 12

30

в)

30 сж. 60

. і

J

11

90 сж 60 30 О

— , ‘ Рис. 12. Изменение с широтой радиации, темпера­

туры и давления. ‘

. а — годовое поступление солнечной радиации к верхней

границе атмосферы на разных широтах; б — среднегодовые температуры поверхности Земли разных широт северного полушария; в — изобара 200 мбар — пример типичного для высот 3—15 км среднегодового наклона поверхности рав­ного атмосферного давления.

300, 400, 500 мбаров. Все показанные на рисунке линии — могут быть приблизительно описаны косинусоидой с ар — тументом 2ф. Например, если обозначить среднее давле­ние по меридиану на высоте h буквой р, а давление на той же высоте h и широте ф знаком р(ц>), отклонение давления от среднего приблизительно выразится форму­лой

Р (?) — р — В cos 2-f, . (54)

где В — амплитуда изменений давления на высоте.

Такой ход Давления должен вызвать перенос возду­ха от экватора в сторону полюсов. Этот перенос дей­ствительно наблюдается и начинается у экватора на вы­сотах 5 км и более. Перенос приводит к оттоку воздуха от экватора и уменьшает массу экваториальной атмо­сферы и ее приземное давление. Одновременно вблизи 30-х параллелей создается нагон воздуха и вызванный им динамический пояс высокого приземного давления атмосферы. <

Необходимо рассчитать этот пёренос, чтобы связать звенья системы управления. Однако вопрос, к которому мы решаемся приступить, труден и не имеет простого решения. Большинство авторов, занимавшихся им, исхо­дили из гипотезы установившегося движения без уско­рений. Его наиболее простой вариант — геострофичес — кое равновесие (см. раздел «Математические модели течений») — не может дать никакого переноса по мери­диану. Тогда к расчетам привлекается боковое переме­шивание атмосферных потоков,’ волны давления и дру­гие сложные процессы.

Мы обратим внимание на другое обстоятельство. На рис. 2 а показана траектория частицы, рассчитанная ме­тодом Лагранжа, с учетом полного ускорения движения. Траектории радиозондов, выпускавшихся’ в зоне эквато­ра, очень близко напоминают форму первой части тра­ектории на рис. 2 а до той точки, где частица, достигнув вершины рисунка, начинает возвратное движение.[14] Та­кого возвратного движения шары-зонды не показывают. Надо полагать, что оно и невозможно. Действительно, — представим, что пространство, занимавшееся частицей, вышедшей из начальной точки траектории (рис. 2 а), мгновенно заполнилось частицей, пришедшей не сбоку, а снизу, как и должно быть на экваторе. Эта новая час­тица устремилась вслед за — первой, за ней движется сле­дующая, и таким образом траектория одной частицы превращается в непрерывную струю воздуха. Но если условия вдоль экватора однородны, то соседние струи заполняют все пространство горизонтальной плоскости.

Пока эти соседствующие струи удаляются от эква­тора, они не будут мешать движению друг друга. Но,
как только одна из них начнет поворачивать обратно, она. столкнется со встречным потоком и будет оста­новлена. Удовлетворившись таким объяснением, попы­таемся рассчитать’первую часть траектории (рис. 2 а), исходя из реальных условий хода давления вдоль мери­диана и учитывая изменение силы Кориолиса с широтой.

Траектория получается из уравнений:

(55)

du у г» . -jf — = uy2<s> sin ср,

(56)

Ось х направлена к востоку, ось у — к северу. Вве­дем в расстояние у широту места: у=сц>, где с — длина одного градуса широты в метрах. Подставим также в уравнение (56) величину давления по формуле (54). После этого уравнения (55) и (56) целесообразно пере­писать так:

(57)

Решение составленных уравнений не сложно, но для рассматриваемой’задачи оно никем не проводилось. Интегрируем (57) по времени t

== 2шс J sin ср —- J dt — j — Сх = — 2о)С cos 9 + Си

(59)

Если движение начинается на линии экватора, то можно записать условие:

(60)

О при 9 = 0°.

Отсюда Ci=2(x)C, а составляющая скорости вдоль Параллели,

(611

— == 2юс (1 — cos <р).

Будем теперь искать составляющую скорости вдоль меридиана. Подставим формулу (61) в уравнение (58):

■ = 4(о2с sin у (cos ср — 1)+ …. Z? sin2cp. (62)

Порядок уравнения (62) понизим путем подстановки:

cd’jj cd2tр dv dv cd<? vdv /соч

dt ~V’ ~dW~ dt ~cdtp dt~~ cdf * " ‘

Тогда уравнение (62) получит вид.

vdv — 4ш2с2 (sin ср cos <рdy — sin <pd<?) +

-J—sin 2<?df. (64)

Интегрируя, найдем: ,

-і — v2 = 2со2с2 sin2 ср -f — 4(о2с2 cos ср •—— cos 2ср + С2. (65)

Учитывая, что на экваторе скорость равна нулю (v = 0 при ф = 0°), определим С2: . .

С2 = —4Л2 + 4-. (66)

И наконец, получим расчетную формулу для нахож­дения скорости переноса по меридиану:

uy = v = 2~[sin2 у (А — (oV У) , (67J

Из условия равенства этой скорости нулю найдем ту широту, на которой прекращается свободное движе­ние частиц к полюсу (верхняя точка траектории на рис. 2 а). Обозначим эту широту через фь

_8 т2г2 I — cos Ф! __ п — в.

о 1 -|- COS фх ’ : : ^1 о)2с2а + В * . ‘ )

Легко решить и обратную задачу — найти амплитуду давления В, необходимую для выхода частицы на за­данную широту фі:

В1 — со2с2о ] 7 cos 91 ■. (69)

. [15] . 1 + COS ср, v ’

Приведём теперь пример вычисления. С январской карты давления на высоте 5 км снимем разность давле­ния между экватором и полюсом 26—70 мбаров. Под­ставим в формуле (68) значения 5i=35- 105г/(м-с2); с— = 111 • 103 м; (0=4,18-10~3 град/с; о=650 г/м3. Находим фі = 18° с. ш. Примерно в этих широтах или несколько южнее начинается пояс высокого давления, достигающий максимума у 30° с. ш. Чтобы получить центр пояса, нуж­но найти среднее фі по высоте атмосферы или внести эмпирическую поправку D.

Допустим, что Это можно сделать так:

= + А (70)

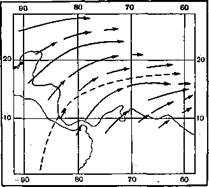
Таким образом, наша система пришла в движение. Неравномерность поступления радиации на поверхность планеты привела к распределению температуры и дав­ления, показанному на рис. 12. Это вызвало меридио­нальный перенос воздуха на высотах, называемый анти­пассатом. Траектории антипассата, наблюденные и рас­считанные по формулам (61) и (67), показаны на рис. 13.1 Схождение потоков антипассата на широте фі соз­дало динамическую зону высокого давления с максиму­мом на широте фі*. Эта зона вызвала систему призем­ных ветров (рис. 11) и систему касательного напряже­ния ветра о воду (рис. 6). Ветер привел субтропические воды в антициклоническое движение с центром, смещен­ным, по теореме Праудмена, к западному берегу океа­на. Величина этого смещения может быть вычислена по полю ветра. Затем вся система течений, не прекращая антициклонического вращения, смещается под действи­ем силы Кориолиса к экватору. Здесь происходит встре­ча вод северного и южного полушарий. Этим вызывает­ся схождение вод, и их избыток, имеющий наибольшую

величину у западных берегов, создает компенсационные течения к полюсам. Наиболее изученным примером та­кого течения служит Гольфстрим. За последние десяти­летия в Тихом океане (1951 г.), Атлантическом (1959г.) и, в Индийском (1960—1963 гг.) у экватора были сде­ланы неожиданные открытия. Оказалось, что на глуби­не, начиная с 50—100 и до 200—400 м под поверх­ностью, существуют узкие (от 2° с. ш. до 2° ю. ш.), но

Рис. 13. Траектория частиц в анти­пассате. . Сплошные стрелки — наблюдения в де­- кабре 1956 г. (по Колону, 1960), пунктир­ ная линия — расчет по формулам (61) и _ (67). .

сильные потоки, пересекающие океаны с запада на вое — ток. В Атлантическом океане — это открытое советски­ми учеными течение Ломоносова. Оно имеет расход, сравнимый с Гольфстримом, — 37 млн. м3/с и скорость около 120 см/с. Скорость такого же течения в Тихом океане 150 см/с,.расход около 40 млн. м3/с. В Индий­ском океане течение имеет сезонный характер, оно раз­вивается зимой северного полушария, во время северо­восточного муссона, и исчезает летом с началом юго-за­падного муссона. В период максимального развития скорость течения в стрежне составляет 60 см/с. Мы вспомнили об этих потоках после того, как заметили, что максимальное схождение вод у экватора должно наблюдаться, в западной части океанов, откуда и дви­жутся эти потоки.

К северу от антициклонической системы, смещаю­щейся к экватору, расположена циклоническая область движения, имеющая тенденцию смещаться к полюсу. Между этими системами в направлении с запада на вос­ток устремляется Гольфстрим.

У читателя может возникнуть вопрос, нельзя ли’оп­ределить области низкого атмосферного давления таким же путем, как и зону высокого, т. е. исходя из измене­ния радиации с широтой.4 Оказывается, нельзя. С при­ближением к полюсу сила Кориолиса возрастает и ус­тойчивые меридиональные движения становятся невоз­можными. Новые области имеют в значительной мере сезонный характер (особенно над материками) и назы­ваются не динамическими, а термическими областями давления.

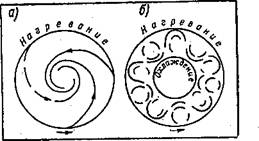
Очень наглядно изменение характера меридиональ­ных движений с увеличением силы Кориолиса демон­стрирует вращающаяся модель известного шведского геофизика К — Россби. В этой модели величина поворот­ной силы Кориолиса подбирается путем изменения ско­рости вращения. Малая скорость соответствует тропи­ческим широтам, высокая скорость умеренным и по­лярным. Воздух в модели заменен водой, которая окра­шивается и подогревается со стороны внешней стенки, ближе расположенной к экватору. При малых скоростях движения на модели видны траектории окрашенных струй, которые соответствуют сделанным выше расче­там антипассата, если перевести цилиндрические коор­динаты модели в декартовы. При больших скоростях вращения упорядоченный характер переноса к полюсу исчезает — развиваются крупномасштабные горизонталь­ные вихри или волны, очень похожие на картины дви­жения в умеренных широтах на высотных синоптиче­ских картах. Два вида траектории частиц в модели по­казаны на рис. 14 а, б. .

Итак, области аномального давления приполярных и умеренных широт имеют непосредственно термическое происхождение, связанное с температурой именно дан­ной области. Над материками эти области в течение го­да меняются.. Зимой здесь высокое давление (антицик­лон), летом—низкое (циклон). Однако над океаном

пониженное давление может сохраняться круглый год. Мы видели это на примере взаимодействия Гольфстри­ма с исландским минимумом давления. Поддерживая этот минимум, Гольфстрим обл. егчает свое проникнове­ние в Арктику.

Здесь мы подходим, возможно, к самому важному звену системы — полярным льдам океана. Значение это­го звена связано с его неустойчивостью. Расчета пока­зывают, что нужно сравнительно небольшое увеличение

Рис. 14. Токи нагре­ваемой с периферии воды на вращающейся модели (рисунок по фотографии из статьи К. Г. Россби, 1959). а — малая скорость вра­щения (тропики); б — большая скорость враще­ния и охлаждение мо­дели в центре (умерен­ные широты).

притока тепла к полюсу, чтобы за несколько лет аркти­ческие льды растаяли. По расчетам крупнейшего совет­ского климатолога М. И. Будыко[16] при положительной аномалии летних температур воздуха,’равной 4°,. «лед толщиной 4 м в средних климатических условиях Цент­ральной Арктики полностью исчезает через четыре го­да». После этого ледяной покров будет иметь сезонный характер, появляясь только во время полярной ночи. Бу­дыко далее пишет: «Ясно, однако, что полученная

здесь оценка аномалии температуры, при которой мно­голетние арктические льды разрушаются, является мак­симальной. ТаК как при сокращении площади льдов на свободной поверхности океана значительно увеличивает­ся количество поглощенной радиации, то после уничто­жения части льдов может произойти дальнейшее увели­чение температуры, которое в свою очередь усилит та­яние льдов».[17]

Уничтожение постоянного ледяного покрова Арктики нарушило бы равновесие всей системы океан — атмосфе­ра. Картину переходного процесса к новому равновесию пытались рассчитать многие авторы. Наиболее извест­ны широкому читателю работы советского инженера и географа П. М. Борисова и прежде всего его книга «Мо­жет ли человек изменить климат» (М., «Наука», 1970. 192 с.). Борисов считает возможным уничтожить льды путем создания «прямотока» (по терминологии Бори­сова) Гольфстрима из Атлантики в Тихий океан через Северный Ледовитый океа! н и Берингов пролив. В этом проливе, имеющем глубину всего около 45 м и ширину около 80 км, Борисов предлагает создать плотину с пе­рекачкой, воды турбинами из Арктики, в Тихий океан. Инженерный проект плотины’опубликован и подсчитан размер финансирования строительства 24 млрд. руб­лей.

Этот проект широко обсуждался учеными, в том чис­ле и на специальной конференции, но одобрения не по­лучил. Мы еще слишком плохо знаем количественные законы взаимодействия звеньев системы океан — атмо­сфера, чтобы решиться на умышленное нарушение ее равновесия. Мы далеко не уверены и в том, действитель­но ли плотина создаст «прямоток» Гольфстрима и улуч­шит климат. .

Однако можно наблюдать неумышленное вмешатель­ство человека в равновесие системы. В первом разделе мы говорили о роли испарения для стабилизации тем­пературы воды. На испарение расходуется около 51 % энергии, поглощаемой океаном с радиацией Солнца. Но испарение может быть замедлено, а местами и прекра­щено, если поверхность воды окажется покрыта мономо — лекулярными пленками. Такие пленки возникают при загрязнении воды нефтью в результате катастроф, очист­ки нефтяных емкостей в океане и главное добычи нефти с морского дна, которая быстро возрастает у берегов океана. .

ПодвОдя итоги проведенному обсуждению о взаимо­действии элементов и звеньев системы управления, вы­делим следующие характеристики: ‘

1) поступление солнечной энергии на поверхность океана R;

2) меридиональные градиенты температуры поверх­ности океана grad.

3) изменение высоты столбов атмосферы A#;

4) градиенты давления в верхней атмосфере grad р

5) меридиональный перенос воздуха антипассатами W(A);

6) пояс высокого давления в субтропиках АР (фі);

7) ротор напряжения ветра в субтропиках rotzt;

8) смещение циркуляции к экватору — rotzxL;

9) компенсационное течение западных берегов гр (Г); . 10) температурная аномалия на границе полярной

области Д’&(ф2);

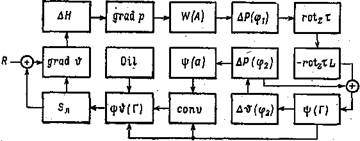
Рис. 15. Функциональная схема управления океанической цир­куляцией. " На входе солнечная радиация создает градиент температуры на 1, поверхности океана..— это дает начало функционированию системы.

11) сезонная область пониженного давления над океаном АР (ф2);

12) вынос арктических вод if> (а);

13) встреча полярных вод с Гольфстримом conv;

14) перенос тепла Гольфстримом в полярные широ­ты т|эФ(Г);

15) загрязнение вод океана нефтью Oil;

16) площадь полярных льдов 5Л.

Взаимные связи между этими переменными показа­ны на схеме (рис. 15). Схемы такого типа называются функциональными схемами системы, а их создание со­ставляет первую задачу системного анализа. Частично связи на схеме (рис. 15) уже теперь могут быть выра­жены в количественной форме, как мы видели на не­скольких примерах. Но в основном их нужно еще опре­делить. Приведенная схема, конечно, очень далека от завершенности, но может быть основой для дальнейших рассуждений.

Мы познакомились с частью работ, относящихся к проблеме конструирования глобальной океанской систе­мы. Они находятся в русле традиционного исследова­тельского подхода, направленного на объяснение связи между явлениями. Но всегда ли необходимо иметь объ­яснение такой связи, знать ее причины и механизм? При сложном характере системы такое требование может стать препятствием для моделирования и прогнозов. Альтернативой к объяснительному подходу служит прин­цип «черного ящика», когда причинный механизм связи между явлениями или не исследуется совсем, или отхо­дит на дальний план и рисуется в виде предположений, не влияющих на расчеты. В то же время сама связь изу­чается и выражается количеств’енной зависимостью, на­пример уравнениями, графиками, таблицами. Именно в таком плане интересна работа Т. К. Ижевского «Си­стемная основа прогнозирования океанологических ус­ловий и воспроизводства промысловых рыб» (М., изд. ВНИРО, 1964, 166 с). Ижевский делил Мировой океан на несколько систем, процессы в которых находятся в противофазе: если в одной системе увеличивается запас тепла, влаги и пищевых ресурсов, то в соседних с нею в это же время происходит их уменьшение. В Северной Атлантике Ижевский выделял три системы, исследова­ние систем велось методом корреляции, и были сделаны долгосрочные прогнозы продуктивности. ~

Приведенные примеры показывают, что решение гло­бальных задач комплексного характера становится те­мой океанологических расчетов.

Комментарии запрещены.