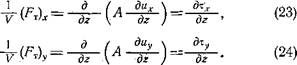Бурение грунтовых зондов, установка энергетических колодцев

Физические основы уравнений. Из школьного курса известно уравнение второго закона Ньютона:

am = F, (10)

где а —ускорение, получаемое телом; т — масса тела; F — сила, действующая на тело.

Подавляющее большинство уравнений, служащих для нахождения скорости (воды, ледников, воздуха), как

бы сложно эти уравнения ни были записаны, не что иное, как расшифровка уравнения (10) в конкретных физических или географических условиях. Это — уравне­ния динамики. ■ . ■ • •" .

Итак, уравнение (10) будет исходным для дальней­ших рассуждений.’ Запишем (10) в дифференциальных обозначениях; ‘

V -^- = F, : (11)

где и — скорость;, ‘т — масса тела; F — действующая сила; t— время; (It — бесконечно малое приращение вре­мени; urn—количество движения; d(wn)— изменение количества движения за время dt. %

Особое написание букв, обозначающих скорость и силу, показывает, что речь идет о векторах, т. е. в дан* ном случае, о величинах, имеющих переменное направ­ление. Под знаком F-в уравнении (11) может подразу­меваться не только одна сила, но и результат геомет­рического сложения нескольких сил — результирующая сила. Чтобы подчеркнуть это обстоятельство, закон Ньютона можно переписать в вцде ’ .

: d{atl) =SF, , (12)

где 2—знак суммы. , .. ■/,

Сложение сил;производится по правилу параллело­грамма. Это означает,-в частности, что если к телу при­ложено одновременно несколько сил, то каждая из них сообщает телу определяемое вторым законом ускоре­ние так, как если бы других сил не было; Напомним еще, что действие — силы сказывается независимо от того, пребывало ли — ранее тело в покое или же дви­галось. ■ ;

Упрощение уравнения Ньютона. Уравнение (12) вме­щает в себя столь большое содержание, что служит основой не только уравнений течений, но и движения КОС’ мических ракет с переменной массой. В динамике сплощ — ных сред (вода, материковые льды, воздух) это урав­нение применяется в упрощенном виде. Поскольку интересующим нас телом является кубик воды (льда, воздуха), вырезанный из потока, его массу можно запи­сать так:

m = aV, (13)

где сг— плотность воды; V — объем кубика.

Если допустить, что для воды, как и для идеального газа, произведение плотности на объем величина посто­янная, то массу в уравнении (12) можно вынести из — под знака дифференциала: —

.0V-§- = 2T. (14)

Упрощенная форма записи (14) вошла в гидродина­мику после работ Эйлера и Даламбера (1750-е годы). Она ’основана на постулате, получившем название «за­кона сохранения массы для элемента движущейся жидкой среды»: —

а 1/= const. . (15)

Очевидно, что уравнение (15) не учитывает измене­ние массы выбранного нами кубика за счет диффузии солей, испарения, нарастания льда и тому подобного, а поэтому будет строгим лишь для бесконечно малого по размерам кубика, который ведет себя относительно на­званных превращений как единое целое. —

Неожиданные трудности — неразрывность среды. До сих пор нам могло казаться, что описание движения частиц жидкости не более трудная задача, чем описа­ние движения твердого тела. Однако в первом случае мы сталкиваемся с неожиданной проблемой — в процессе движения жидкости должно выполняться условие нераз­рывности, или сплошности, ее среды. Иными словами, в потоке не может возникать ни пустот, ни таких прост­ранств, которые заняты сразу несколькими объемами жидкости.

Чтобы не войти в противоречие с этим требованием, часто приходится использовать упрощенные или «идеа­лизированные» условия движения. Допустим, мы хотим получить траектордю какой-то частицы. Построим мо­дель движения так, чтобы силы, действующие — на эту частицу, и частицы, лежащие на ее пути, были в каждый момент времени одинаковы, Тогда соседние частицы бу-

дут двигаться с равными скоростями, и это предотвра­тит их «столкновение» или «разрыв». Именно при та­ких условиях были получены траектории на рис. 2, именно поэтому в расчётах траекторий предпола­галось, что планетарный" вихрь не изменяется на пу­ти. частиц. . ■ •

Проблема, возникающая из-за неразрывности жидко­сти, была рассмотрена в 1755 г. Леонардом Эйлером. Среди получённых Эйлером результатов был новый под­ход к изучению движения жидкости. Раньше мы гово­рили о движении индивидуальной частицы жидкости, и применение к ней второго закона Ньютона было вполне очевидно. Теперь же зададимся другой целью. Будем искать скорости в каком-то неподвижном маленьком объеме пространства. Пусть через этот объем непре­рывно проходят новые частицы воды. Можно ли при­менить для этого случая ньютоновский закон в записи (14)—уже далеко не очевидно. Действительно, новый объект исследования — объем пространства — содержит в каждый момент времени новые частицы материи. Эй­лер разрешил это противоречие, показав, что в новой постановке задачи изменение скорости в точке зависит от дополнительного обстоятельства— инерции приходя­щих сюда частиц. Например, если частицы потока име­ют за секунду до подхода к точке скорость на 1 см/с большую, чем была в точке, они создадут ускорение 1 см/с2.-Поясним это более подробно.

Пусть в потоке, идущем по оси х, скорость в момент времени t в точке Х2 равна и2, а скорость на расстоянии Ах до подхода к точке равна щ. Положим для опреде­ленности Ax=10 см, «2 = 9 см/с, U = 10 см/с. Таким образом, изменение скорости на. расстоянии Ах будет Аи=—1 см/с. Изменение скорости потока в точке Хг за секунду составит

Лйп Аи, /7 ‘

~~КГ~ =~ и ~~KJT = см/с •

Переходя к пределу и трехмерному движению, мы можем записать значение инерционных ускорений:

Значит, полная сумма ускорений в точке равна

du 1 du du du

— ■%*—«Х-Ц7-~ Ъ "

dt ~ qV — «X dx "y dy dz

Если описание движения строится по форме (14), т. е. для индивидуальной частицы, то говорят, что дви­жение рассматривается методом Лагранжа, если по форме (17) —методом Эйлера. В методе Эйлера усло­вие неразрывности имеет простую форму записи:

дйх , &иу, duz А /1о

Ох + Оу + Ог ~0,

Порассуждаем немного об этом уравнении. Пусть имеется неподвижный кубический объем пространства. Две грани куба перпендикулярны оси х, две—оси у, две —оси г.’ За счет движения по оси х в кубе может образоваться прибыль воды, равная AuxAyAz, по оси у — АщАхАг, по оси г — AUzAxAy, где Аи — изменение ско­рости воды при ее движении через куб; Ал:, А у, Az~— ребра куба.

Если вода несжимаема, суммарная прибыль равна нулю:

Аи^ДуДг + киукхкг + = 0.

ДгУ, A uz

Разделим уравнение на величину объема — AxAyAz:

0.

Да’ 1 i_v Дг

Переходя к пределу, имеем (18).

Это уравнение в задачах морских течений обычно удовлетворяется с помощью специального приема. Мы допускаем, что горизонтальное движение (составляющие Ux, Uy) целиком определяется действующими силами и никак не ограничивается условием неразрывности. Од­новременно мы полагаем, что вертикальное движение (ыг) не зависит от действующих сил, а целиком подчи­няется одной задаче —устранить противоречия гори­зонтального движения с условием неразрывности. На­пример, если горизонтальное движение стремится вме­стить несколько объемов жидкости в один и тот же объ­
ем пространства, то противоречие с уелоЁием неразрыв­ности устраняется вертикальным оттоком жидкости из этого же пространства. Если горизонтальное движение создает пустоту в каком-то объеме пространства, этот объем заполняется вертикальным движением воды.

Математически такое согласование с условием нераз­рывности достигается тем, что рассчитывается горизон­тальное расхождение скорости (дивергенция):

. = 09)

а найденная величина подставляется в уравнение (18), откуда и получают вертикальную скорость. Таким обра­зом, во многих задачах морских течений горизонталь­ное движение воды вычисляется так, как — будто бы ус­ловие неразрывности и не существует, а вертикальное так, как будто бы никакие силы в вертикальном на­правлении не действуют.

Силы, вызывающие течения. Посмотрим, какие силы могут действовать на морские воды. Мы уже говорили о поворотной и градиентной силе. Добавим к сказанно­му ранее,-что горизонтальный градиент давления возни­кает в толще воды не. только за счет наклона уровня, но и-за счет изменения температуры или солености, а значит, и плотности воды. Различия в плотности и на­клон уровня создают различия в массе соседних стол­бов воды, а следовательно, и в давлении.

Если на расстоянии dx давление меняется на вели­чину dp, то по оси х возникает движущая сила давле­ния {Fd)x — —dpdxdy, действующая на объем воды V (V=dxdydz). Отнеся эту силу к единичному объему, потучим — —

Знак минус мы ставим потому, что сила направлена от большего давления к меньшему. Горизонтальный

градиент давления есть геометрическая сумма двух сил (20) и. (21). Градиент показывает направление, вдоль которого под действием разности давлений движется

ЖИДКОСТЬ. • . —

Вторая сила, вызывающая течения,—это трение вет^ ра о водную поверхность. Сила трения, отнесенная к единице поверхности, называется напряжением трения и обозначается буквой т. Согласно ньютонову закону тре­ния значение т равно (ось z направлена вниз)

(22)

где А — коэффициент внутренней вязкости воды.

Если мы выделим в толще воды отдельный слой, то очевидно, что в процессе движения он будет испытывать напряжение т со стороны своих верхней и нижней по­верхностей. Если скорость в потоке уменьшается сверху вниз, то трение о слой, приложенное сверху, будет его ускорять, а трение, приложенное снизу,— тормозить. Результирующий, эффект от этих двух воздействий мы найдем, если геометрическую разность между двумя т отнесем к толщине нашего слоя., Переходя к пределу, получим величину силы трения, действующую на объем У. Запишем ее значения по осям х, у, имея в виду слу­чай, когда составляющие вектора скорости меняются только по оси z: ■

Читатель может заметить, что наше рассуждение под­разумевает слоистую (ламинарную) модель течений, и вправе удивиться — неужели такая модель применяется к океану? Да, уравнения океанических течений обычно ‘ строятся именно так, и океанографы моделируют ими осредненное турбулентное движение путем подбора чис­ленных значений величины А, называемой коэффициен­том в, иртуальной (т. е. эквивалентной) вязкости. Имеется в виду, что коэффициент делает ламинарную модель эк­вивалентной турбулентному движению. Иногда о лами­

нарном характере модели забывают и говорят просто «турбулентная вязкость».

Модель Экмана. В 1902 г. шведским ученым В. Экма — ном (в то время студентом) была опубликована став­шая знаменитой модель ветровых течений. Эта матема­тическая модель смогла объяснить непонятное раньше отклонение дрейфа льдов вправо от направления ветра. Такое отклонение наблюдал Ф. Нансен в Северном Ле­довитом океане на судне «Фрам».

«Это отклонение вправо,— писал Нансен,— очевидно, вызвано отклоняющей силой вращения Земли. Странно, что очень мало авторов достаточно осознали факт, что поверхностное течение, созданное ветром, не может сле­довать в направлении ветра, но должно отклоняться вправо; вследствие этого они, говоря о действии ветра на поверхность моря, приходили к неверным результа­там. . ■ ■

Еще меньше обращалось внимание на то обстоя­тельство, что поверхностное течение, созданное ветром, не может увлекать лежащую ниже воду в своем собствен­ном направлении, но вода будет стремиться отклониться вправо и, таким образом, угол отклонения слоев воды будет увеличиваться с глубиной»[6].

Уравнение установившегося ветрового течения Экман записал в виде равновесия по каждой из горизонталь­ных осей координат (х, у) двух сил: силы трения, выз­ванной ветром, и силы Кориолиса, вызванной в^аще — нием Земли. Направим ось х к востоку, а ось у — к се­веру. Предположим, что величина виртуальной вязкости, входящей в формулы силы трения (23) и (24), посто­янна. Отнеся силы к единичному объему, получим

— A-^- = Mya2o)slncp, (25)

_ = _ ахо2со sin ср. (26)

Два написанных уравнения сводятся к одному с по­мощью комплексной переменной. При решении появ­ляются две постоянные интегрирования, которые определяются через граничные условия задачи. Эти усло­вия приняты в модели такими: на глубине z = оо ско­рость течения обращается в нуль; на поверхности (z = 0) выполняется ньютонов закон трения, т. е. касательное напряжение трения ветра о поверхность воды прини­мается пропорциональным сдвигу скорости. Если трение ветра направлено по оси я, то из формулы (22) получим

‘*=-л(-§^>’>=-°- (27)

Читатель, возможно, обратил внимание на то, что в последних уравнениях мы перешли от частных произ­водных к полным. Это означает лишь то, что в данной задаче искомые величины их, щ считаются функция­ми одной независимой переменной г. Таким образом, сама форма записи уравнений (25) — (27) показывает, что Движение не изменяется в горизонтальном направ­лении и во времени. Значит, мы. рассматриваем дейст­вие однородного и неизменного по скорости и направ­лению ветра над безграничным по площади океаном. То что мы вводим граничное условие при z-оо, подразу­мевает безграничную глубину этого условного океана.

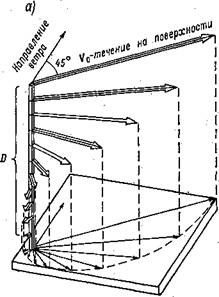
Аналитическое решение уравнений показывает, что скорость с глубиной уменьшается и ее вектор поворачи­вает все более вправо (северное полушарие). При этом линия, соединяющая концы векторов скорости, Образует логарифмическую спираль. Уменьшение скорости не свя­зано с переходом кинетической энергии движения в теп­ло. Оно целиком вызвано силой Кориолиса. На рис. 9 а показана спираль ветрового течения, называемая спи­ралью Эхмана. . , .

Поскольку движение в модели Экмана не имеет ускорений, то сумма сил, действующих на любую час­тицу жидкости, равна нулю, Основываясь на этом поло­жении, мы можем построить конечно-разностным мето­дом собственный вариант спирали, исходя из других граничных условий. Такое построение позволит нам лучше понять физический смысл решения Экмана.

Итак, приступим к построению спиралй. Предполо­жим, что на глубине h происходит скачкообразное уве­личение плотности воды. Это затрудняет турбулентное перемешивание по вертикали. Коэффициент вязкости уменьшается, приближаясь к молекулярному значению.

Допуская некоторую идеализацию условий, положим, что Л=0 при г —h.

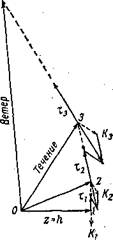
На рис. 9 6 цифрой 1 обозначен вектор скорости в самом нижнем слое течения на глубине /г. Пусть объем воды, для которого мы хотим построить-равновесие сил, расположен на правом конце вектора, там, где помечена стрелка.

Поскольку этот объем движется, то на него будет действовать сила Кориолиса, направленная перпенди-

Рис. 9. Ветровые течения, а —модель Экмана, 1902; б — течение, срезанное на глубине Л скачком плот** . . ’ пости.

кулярно скорости и пропорциональная её’ величине и массе воды в объеме. Обозначим эту силу Ки.

Так какобъем не имеет ускорений, сила Ki должна быть уравновешена противоположно направленной си­лой ть Эта сила, очевидно, вызвана трением о вышеле­жащий слой воды. Согласно гипотезе Ньютона о. внут­реннем трении в жидкости; «сопротивление, происходя-

щее от недостатка скользкости жидкости при прочих одинаковых условиях, предполагается пропорциональ­ным скорости, с которой частицы жидкости разъеди­няются друг от друга».[7] ~ ,

Векторы скорости /, 2, 3 показывают путь частиц воды, а вектор 4 — путь частицы воздуха за единицу времени, поэтому скорость разъединения частиц будет равна расстояниям 1—2, 2—3, 3—4. Пропорциональность этих расстояний величине трения зависит от величины вязкости А. Допустим, что в нашем случае величины от­резков 1—2, 2—3 относятся к величине трения как 2:1. Это трение внутри воды. Пусть сцепление между возду­хом и водой имеет меньшую величину и, в соответствии с этим, длина отрезка 3—4 относится к величине каса­тельного напряжения ветра как 3:1.

Основываясь на условно взятых пропорциях (мы могли бы их вычислить, зная величину А), восстановим из точки / перпендикуляр 1—2. Его длина будет вдвое превышать длину вектора трения Гь Соединив точку 2 и 0, получим вектор. скорости второго снизу слоя воды.

Частица воды, расположенная в точке 2, также должна находиться в условии равновесия сил. Эти силы будут К2, Ті, Гг. Нанеся-их на рисунок, найдем конец следующего вектора (точка 3) и, продолжая построек ние, получим величину и направление скорости ветра (вектор 0—4), а также величину и направление вектора трения ветра о воду (касательное напряжение ветра Тз).- Как бы ни строились спирали ветрового течения, они обладают тем общим свойством, что результирующий по вертикали перенос вод направлен под прямым углом вправо от вектора трения ветра о воду.[8] Воздействие силы Кориолиса приводит к тому, что чисто ветровые течения быстро затухают с глубиной. Их толщина имеет порядок 100 м. ‘

Комментарии запрещены.