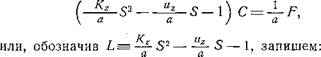Бурение грунтовых зондов, установка энергетических колодцев

. … Четыре фактора можно считать первичными

регуляторами природы: энергия, вещества, услот. вия существования и сообщество. [37]

Е. Одум

‘ ‘ * і. •

Мы. представляем в общем виде схему взаимо­действия природных процессов, действующих на поверхности Земли, в океане и атмосфере, но • наши сведения о количественных соотношениях

в этих связях и в особенности о связях типа управления пока еще отрывочны и примитивны. Таким образом, мы воздействуем на природу, но. в то же время еще плохо понимаем, каковы

. будут проистекающие ог этого следствия, ii, как

? правило, не считаемся с ними.[38]

, Е. Федоров

Определим самую примитивную зависимость на­сыщения океанских вод питательными солями от гидро­динамических процессов (перемешивания воды и ее вер­тикальной скорости) с учетом глубины, на которой кон­центрация питательных солей не меняется по сезонам (это может быть дно или слой скачка плотности).

Если вырезать в воде какой-то неподвижный объем пространства и предположить, что концентрация пита­тельных солей меняется в нем за счет перемешивания воды, вертикального движения и жизнедеятельности планктона, то уравнение баланса питательной соли С можно записать так: ,

дС т, д2С дС „п

■Kz л 2 uz, аС, (105)

dt z dz2 г дг

где — суммарное изменение концентрации соли в

u*(J ‘

объеме; Kz изменение концентрации, вызывае­мое вертикальным перемешиванием ВОДЫ (Кг— коэффи­циент диффузии, показывающий интенсивность переме — . дС

шивания)uz — qj — .изменение, вызываемое вертикаль­ным движением воды (их— вертикальная составляющая скорости течения); аС — изменение концентрации, вызы­ваемое жизнедеятельностью планктона и пропорци­ональное количеству питательной соли.

Допустим, что суммарное изменение концентрации целиком вызывается жизнедеятельностью планктона. Тогда уравнение (105) распадается на два:

<РС иг dC

(106) (107)

dz2 Kz dz

Решение уравнения (106) уже подробно рассматри­валось. Решение же уравнения (107) будет зависеть от величины соотношения, называемого числом Пекле: 1

где Я — расстояние до некоторого источника питатель­ных солей, т. е. до того горизонта, где концентрация пи­тательных солей постоянна, например расстояние до дна или до слоя глубинных вод.

Вид соотношения связан с тем, что при вертикальном движении питательные соли переносятся по оси z не раз­бавляясь, а при перемешивании разбавляются пропор­ционально удалению от источника. Поэтому нужно ис­кать не простое соотношение двух величин Uz и Kz, а со­отношение, взятое с учетом влияния этих величин на пе­ренос питательных веществ. Учет достигается делением Kz на глубину места (или расстояние до источников со­лей) Я, ‘

Решением уравнения (107) будет следующая фор­мула: .

где С*— концентрация питательной соли в безразмер­ных единицах.

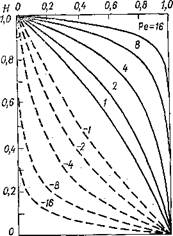
Скорость течения, направленную вверх, будем счи­тать положительной, вниз — отрицательной. В соответ­ствии с этим и число Пекле будет иметь или положи­тельные, или отрицательные значения. На рис. 46 пока­заны распределения концентрации при числах Пекле» равных 16*г 8; 4; 2; 1; 0; —1; —2; —4; —8; —16.:

Рис. 46. Структура океанической «почвы» в зависимости- от числа Пекле (соотноше­ния вертикальной скорости, интенсивности, перемешивания и расстояния до источ — ‘ ника). Сплошные линии — вертикальное распределе­ние питательных солей в богатых (дивергентных) шочвах», пунктирные — в бедных (конвергент­ных) «почвах». Цифрами показаны числа Пекле (Ре = и: К : Н). .

Рисунок построен таким образом, что в него можно подставить любые значения С, Kz, uz, Н, z, так как вме­сто расстояния до источника в метрах по оси ординат отложено безразмерное расстояние в долях от величи­ны Н, принятой за единицу. По оси абсцисс вместо аб­солютной концентрации в миллиграммах на 1 см3 отло­жена безразмерная концентрация, выраженная в долях

Положение круговоротов Океаничес — и среднее содержание кие

Площадь круговоротов, млн. км[39]

зоопланктона, т/км2 фронты

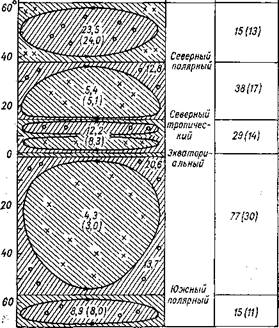
Рис. 47. Конвергентные и дивергентные «почвы» океана.

единицы. При этом за единицу взята разность между высокой и постоянной концентрацией на глубине Я и по­ниженной, но тоже постоянной в данный сезон концен­трацией на поверхности океана.

Из рисунка видно, что плодородие океанской почвы, насыщенность ее питательными солями, существенно за­висит от направления вертикальной скорости.

Вертикальные движения связаны со сгонами и наго­нами или дивергенциями (расхождениями) и конверген­циями (схождениями) морских вод, направлением вет­рового течения и положением берега. Суть здесь заклю­чается в том, что течение, идущее в антициклоническом направлении (т. е. по часовой стрелке в северном полу­шарии), имеет циклоническую завихренность, или ро­тор скорости, в прибрежной зоне от стрежня потока к берегу.

В то же время в центральной части круговорота завихренность скорости носит антициклонический ха­рактер. В циклоническом круговороте — все наобо­рот. .

Циклоническая завихренность означает увеличение скорости слева направо, если смотреть вдоль потока, — и это благодаря силе Кориолиса приводит к сгону (ди­вергенции) вод. Антициклоническая завихренность озна­чает уменьшение скорости — слева направо и, сле­довательно, при ветровом течении произойдет на­гон (конвергенция) вод за счет той же силы Кориолиса.

На рис. 47 показаны зоны дивергенции и конверген­ции. Проставленные на них цифры показывают среднее содержание в воде планктонных организмов в тоннах сырого веса на 1 км2 поверхности океана. Цифры отно­сятся к верхнему стометровому слою моря. Они осред — няют многочисленные наблюдения на научных судах (эти осредненные расчеты проведены в МГУ И. А. Суе — товой). При сравнении рис. 46 и 47 видно, что между гидродинамикой вод, балансом биогенных элементов и биологической продуктивностью океана существует тес­ная связь и что на уравнение (105) можно смотреть как на один из самых простых мостов,-соединяющих гидро­динамические, химические и биологические системы океана..

Уравнение (105) значительно упрощает развитие со­бытий в реальном океане. Действительное положение вещей полнее отразила бы такая запись:

дС „ д2С дС

— Z~dz5 М2 дг " ЬСц, (110)

где Со •— концентрация питательных элементов, заклю­ченных в детрите в 1 л морской воды, (примем Со = = const); ЬСо — скорость их перехода из детрита в мор­скую воду, предполагаемая постоянной по глубине.

При условиях стационарности уравнение (110) мож­но записать в виде уравнения ■

«С=»с,. (Ш)

Если учесть, что концентрация детрита меняется не

сильно, то общим решением этого уравнения будет:

С— + C2er*z + В, (112)

где В, Ci, C2 — постоянные, а гь. г2 — корни алгебраи-.

ческого характеристического уравнения.

КхГ2 ■— иг — а = 0,

получающегося заменой С и производных на степени г

, „ ndC ■ , d2C

(т. е. С на г на г и на г2).

Или еще лучше вместо уравнений (110) и (111) за­писать выражение более общего характера:

Ъ^~а*-1&—аС = р’- (113>

где F — любая функция, аргументом которой не явля­ется С, отражающая, вообще говоря, любое воздействие на систему на различной глубине.

Решение уравнения (113) можно получить класси­ческим путем, аналогично предыдущему, только В, в за­висимости от F, может оказаться и не постоянной, на­пример: .

В = В0 cos юjZ — f — 5j sin WfZ при F=bsin ауг.

Можно получить решение и операторным — методом» очень популярным среди специалистов по автоматиче-

скому регулированию. Покажем, не решая уравнение до? конца, почему этот метод мог бы оказаться полезным: при изучении интересующей нас системы.

Если воспользоваться символом 5 для операции диф­ференцирования^^ ~ , S2= ~^£г> то

aL

с

F.

■О

Первый сомножитель — передаточная функция си­стемы, а второй— входная функция F. Передаточна»

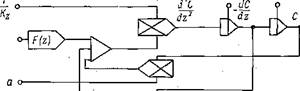
Рие. 48. Блок-схема решения уравнения (113) на аналоговой вычислительной машине.

функция состоит из сомножителя I/а, определяющего) коэффициент усиления системы, и сомножителя 1/L, оп­ределяющего пространственно-динамические свойства си­стемы. Таким образом, операторный метод не только’ удобен, но и нагляден. Это уравнение легко решить на. аналоговой машине (рис. 48).

Но и этот мост между системами весьма примити­вен. Действительные связи между физическими, хими­ческими и. биологическими системами многообразны. При увеличении числа отображаемых в модели элемен­тов системы и связей между ними порядок дифференци­альных уравнений повышается, они могут стать нели­нейными уравнениями, аналитическое решение которых получить обычно невозможно.

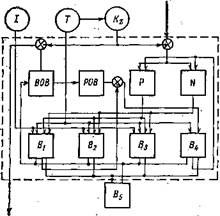
Некоторое представление о сложности реальной си­стемы дает рис. 49. Здесь учитываются средние концен­трации в продуктивном слое моря органического веще­ства, оседающего. детрита, питательных солей (фосфа­ты и соединения азота) и биомассы двух основных ви­дов фитопланктона и бактерий, а также влияние света, температуры и вертикального переноса питательных со­лей из глубоководной части, где их концентрация при-

Рис. 49. Блок-схема связей в си­стеме — фитопланктон — органиче­ские вещества — бактерии —. биоген­ные элементы —. /-г-освещенность; Т — температура; К2 — интенсивность перемешивания; В,, В2 — диатомовые водоросли; В3 — водорос­ли динофлагелляты; В4 — бактерии; В5 — зоопланктон, ВОВ — детрит; РОВ — раст-. воренное органическое вещество; Р—фос — фор; N — азот.

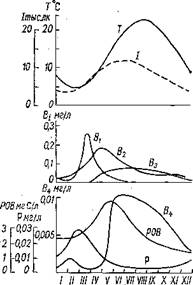
нимается постоянной. На цифровой — вычислительной ма­шине рассчитывались сезонные изменения в системе, и ЭВМ неплохо имитировала реальные события (рис. 50). Необходимо подчеркнуть, что действительные связи в системе еще многообразнее и сложнее. Но можно ли до бесконечности усложнять модель? Она станет необозри­мой и мало полезной. Можно перечислить «бесконечное» число параметров, которые и физикам, и химикам, и био­логам важно учесть. А неизбежные случайные воздей­ствия извне и в самой системе? Очевидно, что на помощь должны прийти статистические и вероятностные модели. Рассматривавшиеся в этой книге модели, основанные на дифференциальных уравнениях (их называют еще «жеет-

Рис. 50. Сезонные изменения в мор­ской экологической системе (резуль­таты моделирования на ЭВМ). Уел. обозначения см. рис. 49.

кими» и «детерминистическими»), позволяют сделать не­малое—привести в порядок имеющиеся сведения и про­верить, как они согласуются между собой и не противо­речат ли действительности. Но это только начало пути.

Комментарии запрещены.