Бурение грунтовых зондов, установка энергетических колодцев

Дисперсионный метод определения <п>. Этот метод, впер­вые предложенный в СССР в 1956 г. М. Т. Прилепиным (позд­нее, в 1965 г., этот же метод был независимо разработан в США П. Бендером и Д. Оуэнсом), основан на использовании дисперсии света в атмосфере. Идея метода заключается в том, что измерение метеорологических элементов во всех точках трассы (невыполнимая задача) заменяется измерением разно­сти оптических путей двух различных длин волн света, кото­рая оказывается зависящей от среднеинтегрального значения показателя преломления воздуха.

Поясним сущность метода. Пусть имеются два источника, из-

лучающие свет различных длин волн Лі и Х2. Среднеинтеграль­ные показатели преломления на трассе D для этих длин волн вследствие дисперсии будут также различны: <П> и

<п2>. Поэтому эти две волны, пройдя одно и то же геометри­ческое расстояние Д пройдут различные оптические пути S = = D<rii> и S2 = D<n2>, а их разность будет

AS = S1-S2 = D((n1)-(n2)). (2.35)

Величины <tii> и <п2> выражаются формулами:

1 D

<«i> = — Г n1(x)dx;

D о 1 °

<«2>=— Г /Ц(х)Дх.

D 0J

В этих уравнениях подынтегральные текущие показатели пре­ломления Яі(х) и пг(х)—показатели преломления для длин волн А.1 и %2 — в каждой точке трассы подчиняются формуле Баррелла и Сирса вида n—f(T, Р, е). Если бы эта функция была линейна по всем переменным, ее можно было бы без ущерба для строгости обобщить на среднеинтегральный пока­затель преломления, т. е. записать в виде <ri> =f(<T>, <Р>, <е», где <Т>, <Р>, <е>—среднеинтегральные значения температуры, давления и влажности. Однако данная функция нелинейна относительно температуры, так как послед­няя находится в знаменателе дроби (см. формулу (2.24)). Но мы можем воспользоваться тем обстоятельством, что функ­ция линейна относительно величины » и записать: <га> =

=f((~т), ®)’ кроме того, для упрощения вывода отбросим

пока влажностный член в формуле Баррелла и Сирса (2.24). Тогда для <Пі> и <«2> можно записать:

W-l=-g-(я*-!)(-£->. (2.36)

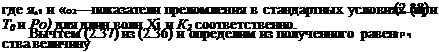W-l=-£-0*-l)(f). (2-37)

где Д«=<«і>—<«2>, Д«о=«оі «02» Подставляя уравне-
ниє (2.38) в выражения (2.36) и (2.37), найдем:

А п

Апф

Учитывая, что в соответствии	с формулой (2.35)	% Q II с <
перепишем последние два равенства в виде:
<«1>—і =	-A AS • ~Al D ’	(2.39)
<«*>-!	-A AS -а2 d,	(2.40)
где
д —	п01 — 1	(2.41)
Л1	A/io *
Ал —	«02— 1	(2.42)
	Д«о

<«2>—1 =(«02 —І)’

А п Дл®

— постоянные для двух данных длин волн А, і и Яд коэффи­циенты, которые можно вычислить по дисперсионным форму­лам. Очевидно, что Ач=А—1. ^

Опуская индексы I и 2 в выражениях (2.39) — (2.42), мо­жем записать их в обобщенном виде:

где По — стандартный показатель преломления для той длины волны, для которой вычисляется <п>.

Выражение (2.43) — основная формула дисперсионного ме­тода. Мы видим, что в нее не входят метеоэлементы, зато вхо­дит разность оптических путей AS.

Расстояние D в этой формуле нужно знать с точностью, ко­торая заведомо будет обеспечена из обычных измерений свето­дальномером.

Основная трудность при реализации дисперсионного ме­тода— высокие требования к точности измерения разности оп­тических путей AS. Непосредственно из уравнения (2.43) для

ошибок получим:

(2.45)

Сделаем оценку для длин волн Л-i = 0,44 мкм и Яг = 0,63 мкм (гелий-кадмиевый и гелий-неоновый лазеры). По дисперсион­ной формуле Коши для группового показателя преломления найдем величины п0 — 1 и Ап0, необходимые для вычисления коэффициента А по формуле (2.44). Для указанных длин волн получим: п0—1=3* 10-4, Дло=14*10-в и 20. Зададим тре­буемую точность определения <п>, т. е. ошибку т<„>, вели­чиной 1 • 10-6, а длину трассы возьмем, например, 10 км. Тогда по уравнению (2.45) получим, что разность оптических путей требуется измерять с ошибкой не более 0,5 мм. При увеличе­нии длины трассы допустимая ошибка тд$ линейно возра­стает. Из уравнения (2.45) видно, что чем больше коэффициент А, тем жестче допуск на точность измерения разности оптиче­ских путей. Поэтому следует стремиться к максимальному уменьшению этого коэффициента. Он зависит от выбора длин волн А,1 и чем больше они разнесены по спектру, тем больше разность Ап0 и, следовательно, тем меньше А. Учиты­вая крутизну кривой п0 (см. рис. 17), можно заключить, что особенно выгодно продвигать меньшую длину волны возможно дальше в коротковолновую область. При этом, однако, прихо­дится учитывать пропускание оптики и атмосферы, практиче­ски не позволяющее использовать длины волн короче 0,35— 0,4 мкм. Большую длину волны также нецелесообразно выби­рать более 0,8 мкм, т. е. за границей видимого спектра, так как в этой области крутизна кривой п0(к) очень мала и, кроме того, мала чувствительность ФЭУ (см. § 13), обычно применяемых в качестве фотоприемников. В большинстве су: ществующих двухволновых приборов используются длины волн 0,4416 мкм (лазер на He-Cd) и 0,6328 мкм (лазер на He-Ne), которые, по-видимому, можно считать оптимальными.

При выводе формулы (2.43) мы допустили упрощение, опу­стив влажностный член в формуле Баррелла и Сирса (2.24). Вывод с учетом этого члена дает полную формулу для двух­волнового дисперсионного метода:

(2.46)

где

В = Дщ>(Л—Ае)

Ро — показатель преломления водяных паров при Т0 и Ро для той длины волны, для которой вычисляется <п>; Аро—раз­
ность величин р0 Для Яі и Ля. Заметим, что коэффициент Ае для водяных паров аналогичен по своей структуре коэффици­енту А для сухого воздуха.

В полной формуле (2.46) присутствует метеорологический

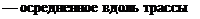член, содержащий величину

значение отношения влажности и температуры. Однако, как следует из анализа точности этой формулы, теперь это значение достаточно знать довольно приближенно, а именно, оно может быть определено по измерениям влажности и темпе­ратуры лишь на концах линии.

Двухволновый дисперсионный метод с учетом влажности по измерениям в конечных точках может обеспечить точность оп­ределения <п> до 1 • 10-7. Дальнейшее повышение точности двухволнового метода может быть получено только за счет бо­лее точного учета среднеинтегрального значения влажности на трассе. Другими словами, для этого уже нужно знать вели­чину (-—) с такой точностью, которая не обеспечивается измерениями влажности только в двух конечных точках трассы [8].

Аппаратурный путь повышения точности определения сред­неинтегрального показателя преломления заключается в при­менении трехволнового варианта дисперсионного метода, в ко­тором для учета влияния влажности к двум оптическим длинам волн добавляется третья, лежащая в диапазоне санти­метровых радиоволн. При этом должны быть измерены две раз­ности оптических путей: разность путей двух световых волн и разность путей одной из световых волн и радиоволн. Третья длина волны выбирается в сантиметровом радиодиапазоне по той причине, что в нем зависимость показателя преломления от влажности на два порядка больше, чем в оптическом диа­пазоне, и поэтому разность оптических путей световой волны и радиоволны будет определяться влажностью в гораздо боль­шей степени, чем при использовании только оптических волн.

Трехволновый метод, однако, труден в реализации, так как он требует весьма сложной аппаратуры, и в настоящее время получил развитие главным образом двухволновый дисперсион­ный метод.

Прибор, реализующий дисперсионный метод, называется ре­фрактометром (в оптике так всегда называется прибор для определения показателя преломления). Рефрактометр обычно строится на том же принципе, что и фазовый дальномер: раз­ность оптических путей преобразуют в разность фаз двух радио­
частотных колебаний с последующим измерением ее радиотех­ническими методами.

Совмещение рефрактометра и дальномера в одном приборе позволяет создать дальномерную систему с коррекцией за по­казатель преломления воздуха, т. е. систему для измерения непосредственно геометрического расстояния D[9]. Такую систему часто называют системой дальномер-рефрактометр или двух­волновым светодальномером, а результат измерения такой си­стемой— геометрическое расстояние D — часто называют кор­ректированным расстоянием. Аналитическое выражение для корректированного расстояния при двухволновом методе вы­текает из формулы (2.46). Умножив обе ее части на D и учи­тывая, что D<n>=S (оптический путь), получим: *

D = S— A AS—(2.49)

где S, А и В берутся для одной и той же длины волны (для Я.1 или для Яг). Следовательно, корректированное расстояние получается в двухволновом светодальномере по результатам измерения двух величин: оптического пути 5 (т. е. расстояния, полученного с использованием скорости света в вакууме, S =

= ~2^) Н3 лю^ов из ДВУХ длин волн и разности оптических пу­тей AS для этих двух длин волн. Величина D0 в уравнении (2.49) есть приближенное значение измеряемого расстояния, которое необходимо знать примерно на четыре порядка менее

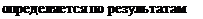точно, чем <п>. Значение

измерений температуры и влажности на концах линии.

Исходя из формулы (2.49) для корректированного расстоя­ния, нетрудно установить, что разность оптических путей должна быть измерена в А раз точнее, чем сам оптический путь. Это приводит к соответственно высоким требованиям к точности фазовых измерений, и единственный путь к сниже­нию этих требований — увеличение частоты модуляции. По­этому в двухволновых светодальномерах выгодно использовать СВЧ модуляцию света. Максимальное значение частоты моду­ляции, использованное в существующих двухволновых прибо­рах,— около 3 ГГц (терраметр, см. § 15, стр. 186).

Более полные сведения о дальномерной рефрактометрии приведены в работе [19].

Комментарии запрещены.