Бурение грунтовых зондов, установка энергетических колодцев

Показатель преломления воздуха

Показатель преломления. Фазовая и групповая скорости. Скорость электромагнитных волн в реальной среде v связана со скоростью света в вакууме с через одну из важнейших ха­рактеристик среды — показатель преломления п:

v^c/n. (2.10)

Показатель преломления в электродинамике определяется из соотношения п = "J/"єр.. где е и р, — диэлектрическая и маг­нитная проницаемости среды.

Различают два понятия скорости электромагнитных волн в среде, вводя представления о фазовой и групповой скоро­стях. Понятие фазовой скорости относится к идеальной моно­хроматической волне. Уравнение такой волны, распространяю­щейся в направлении х, есть A cos (<at—kx), где k = 2л/% — вол­новое число. Фазовая скорость і»ф характеризует, скорость перемещения фазы {a>t—kx) и определяется как dx/dt из усло­вия (d)t—kx) = const, что дает

пф = <*/* = */. (2.11)

Фазовой скорости Цф соответствует фазовый показатель пре­ломления:

щ, = сЬ$. (2.12)

Фазовый показатель преломления, а следовательно, и фазовая скорость в среде зависят от частоты (длины волны), и эта зависимость называется дисперсией.

Реальная электромагнитная волна не является монохрома­тической, а состоит из набора волн различных частот со, груп­пирующихся в некотором спектральном интервале А©. Если А©<С©, то такой набор называют группой волн или волновым пакетом. Излучение, представляемое группой волн, называется квазимонохроматическим. Типичный пример квазимонохрома­тического излучения — излучение лазеров. Уравнение группы волн, т. е. квазимонохроматической волны, с центральной ча­стотой ©о записывается в виде

Ю0+ Ао/2

Е(х, t) = Е0 cos (ю/—kx) da>. (2.13)

©о— A ©/2

Отдельные монохроматические составляющие группы £ocos(cof—kx) распространяются в среде с различными фазо­выми скоростями из-за дисперсии. Поэтому для характери­стики движения квазимонохроматической волны как целого вводят понятие групповой скорости, определяемой выраже­нием

*-(-£-). <2л4>

(индекс 0 означает, что производная берется в точке k = k0t т. е. для центральной составляющей спектра)[5]. Групповая ско­рость характеризует скорость переноса энергии группой волн. Величина

Прр — cIvy р (2# 15)

называется групповым показателем преломления среды. Груп­повая и фазовая скорости и соответственно групповой и фазо­вый показатели преломления связаны соотношением Рэлея:

»гр—»»+<“• )’ (2.16)

или

(2.17)

где -^L ИЛИ ———— дисперсия.

d(o dX

Реальную группу волн (2.13) с центральной частотой ©о можно представить (используя разложение £(<») в ряд) как волну частоты со0, распространяющуюся с фазовой скоростью

ая распро

Направление распространения волны всегда определяется ее фазовой скоростью, энергия же перемещается с групповой ско­ростью. Групповая скорость, таким образом, есть скорость по­тока энергии, или скорость сигнала, и не может быть больше скорости света в вакууме. Фазовая скорость может быть и больше скорости света в вакууме, но она не может быть ско­ростью реального сигнала.

Важно отметить, что понятие групповой скорости приме­нимо лишь к случаю узкого спектра Аю и к среде со слабой дисперсией (именно такой средой является атмосфера, если только длины волн излучения не попадают в полосы поглоще­ния атмосферных газов). Если источник излучает широкий спектр, например белый свет, то физически бессмысленно го­ворить о единой групповой скорости для всего спектра. В этом случае каждый небольшой спектральный интервал, для кото­рого справедливо условие Дю-Сю, характеризуется своим зна­чением групповой скорости; из этих значений можно затем найти эффективное значение групповой скорости (см. далее),

которое и принимается за характеристику скорости распро­странения всего излучения.

Для радиоволн нижний слой атмосферы примерно до 11 км (тропосфера) является практически недиспергирующей средой. Поэтому для радиоволн фазовая и групповая скорости в тро­посфере совпадают.

Для оптического диапазона волн атмосфера является дис­пергирующей средой, вследствие чего фазовая и групповая ско­рости не совпадают. В светодальномерах используется модули­рованное излучение и должна фигурировать групповая ско­рость. Поэтому в светодальнометрии нас всегда интересует групповой показатель преломления воздуха.

При интерференционных измерениях, выполняемых оптиче­скими интерферометрами, используется немодулированное из­лучение[6]. При этом, как было показано специальными иссле­дованиями [22], в отношении. скорости дело обстоит различным образом при абсолютных (лазерных) и относительных интер­ференционных измерениях. В лазерной интерферометрии со счетом интерференционных полос должна использоваться фа­зовая скорость, а при относительном методе интерферометрии с источником белого света — групповая скорость для средней, точнее, эффективной длины волны (об эффективной длине волны см. ниже).

Как следует из уравнения (2.10), задача определения рабо­чей скорости целиком сводится к нахождению показателя пре­ломления воздуха. Вместо показателя преломления п очень часто пользуются более удобной величиной N= (п—1) • 106, на­зываемой индексом преломления. Индекс преломления показы­вает, на сколько миллионных долей показатель преломления больше единицы. Одну миллионную долю — единицу шестого знака — часто называют N-единицей.

Показатель или индекс преломления для электромагнитных волн зависит от длины волны, температуры, давления и со­става воздуха. Зависимость от длины волны (дисперсия), как ясно из вышеизложенного, проявляется лишь в оптическом диапазоне.

Состав воздуха в общем довольно постоянен, за исключе­нием количества водяных паров. Поэтому можно считать, что воздух состоит из двух компонентов — сухого воздуха и водя­ного пара, а индекс преломления воздуха является суммой ин­дексов преломления сухого воздуха и водяного пара:

N = NC + NB. (2.18)

В то время как индекс преломления сухого воздуха имеет один и тот же порядок величины для света и радиоволн (при­
мерно 270—300 yV-единиц), индекс преломления водяного пара для радиоволн примерно в 20 раз больше, чем для световых волн (~60Л^-единиц для радиоволн и ~ЗУУ-единиц для света), а ошибка в определении давления водяных паров, как мы уви­дим далее, влияет на индекс преломления в радиодиапазоне примерно на два порядка сильнее, чем в оптическом диапазоне. Поэтому учет влияния влажности воздуха особенно важен при использовании радиоволн.

Рассмотрим влияние различных факторов на показатель преломления воздуха в оптическом и радиоволновом диапа­зонах. .

Показатель преломления для световых волн. Для оптиче­ского диапазона показатель преломления воздуха в каждой точке является функцией четырех параметров:

л = /(Я, Т, Р. е), (2.19)

где Я — длина волны излучения; Г— температура; Р — давле­ние; е— влажность воздуха (парциальное давление водяных паров).

Обычно рассматриваются раздельно зависимости показа­теля преломления от длины волны и от метеорологических элементов.

Зависимость п от Я (дисперсия) многократно изучалась при определенных, создаваемых в лаборатории метеорологических условиях. Такие условия называются стандартными. Стандарт­ные значения температуры, давления и влажности будем обо­значать Го, Ро и е0. Международными стандартными условиями считаются следующие: Г0=288,16 К ([7]о= + 15 °С), Р0=

= 760 мм рт. ст.*, е0 = 0 (сухой воздух), 0,03% содержания уг­лекислого газа в воздухе. Очень часто при составлении таблиц пользуются стандартными условиями, отличающимися от меж­дународных величиной температуры — 0 вместо 15 °С, т. е. Г0=273,16 К. Дисперсионная зависимость может быть пред­ставлена либо в форме Коши:

W. — * +(2.20)

либо в более общей форме Зельмейера:

(2.21)

где No— индекс преломления в стандартных условиях; Я — длина волны в вакууме; о= 1/Я — спектроскопическое волновое число в вакууме, а величины А, В, С, А’, В’, С’, а, b есть экс­периментально определенные постоянные, называемые диспер­сионными коэффициентами. В радиогеодезии наиболее употре­
бительно выражение в форме Коши, называемое обычно про­сто формулой Коши.

Формула (2.20) относится к фазовому показателю (ин­дексу) преломления. Чтобы получить выражение для группо­вого показателя преломления, нужно воспользоваться соотно­шением Рэлея (2.17). Дифференцируя уравнение (2.20) по X и подставляя результат в формулу Рэлея, получим для груп­пового индекса преломления:

*о = (я, -1) 10е = А + • (2.22)

Значения дисперсионных коэффициентов зависят от того, какие приняты стандартные условия.

Наиболее точной (до 5*10-8) дисперсионной формулой в настоящее время считается формула, коэффициенты которой получены Эдленом в 1966 г.

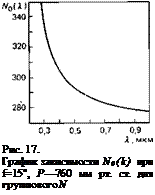
Она выражена в форме Зельмейера, однако удобнее ее пре­образовать в форму Коши. На рис. 17 представлена графически формула Коши для группового индекса преломления при t= = 15°, Р = 760 мм рт. ст. с дисперсионными коэффициентами по Эдлену:

*005.760) = 272,613 + 3- Д|94_ +5. A^L.’ (2.22′)

Для перехода к условиям /=0 °С, Р = 760 мм рт. ст. все коэф­фициенты умножаются на отношение абсолютных температур 288,16/273,16 и формула получает вид

В приведенных формулах длина волны X выражается в мкм.

Таким образом, по дисперсионным формулам можно опре­делить стандартный показатель преломления, зная длину волны света (в вакууме).

Нелазерные источники света генерируют излучение с широ­ким спектром длин волн. В этом случае необходимо находить так называемый эффективный показатель преломления пЭфф, который характеризует весь действующий диапазон спектра от Xi до Хг и описывается выражением

. ——— — ч»- ш— "■ *

где По(Х) определяется формулой (2.22), а величина К(Х)

есть текущая ордината результирую­щей кривой, получаемой как произве­дение спектральных характеристик ис­точника света, оптики, атмосферы и приемника света. Длину волны, соот­ветствующую максимуму результи­рующей кривой спектральной прозрач­ности, называют эффективной длиной волны А, Эфф, т. е. показатель Пэфф отно­сится К ДЛИНе ВОЛНЫ Лэфф.

Таким образом, имея соответствую­щие спектральные характеристики, можно графически определить ХЭфф, которую и следует подставлять в дис­персионную формулу. Тогда получае­мый по дисперсионной формуле пока­затель преломления будет соответствовать эффективному зна­чению, определяемому выражением (2.23).

Неточное знание спектральных характеристик указанных элементов, главным образом характеристики атмосферы, зави­сящей от очень многих внешних факторов, приводит к затруд­нению при определении эффективной длины волны. Практиче­ски эффективную длину волны можно определить лишь при­ближенно, пользуясь некоторыми средними спектральными кривыми. Исключение составляют лазерные дальномеры, в ко­торых вследствие практической монохроматичности лазерного излучения эффективная длина волны равна длине волны излу­чения лазера, известной с высокой точностью.

Для зависимости показателя преломления от метеоэлемен­тов в условиях, отличающихся от стандартных, предложено несколько формул. При светодальнометрии наиболее приме­няемой является формула Баррелла и Сирса, которую для группового индекса преломления можно представить в прибли­жении

N = N0—^—^-— (17,045——- -4^—) —=г » (2.24)

Р0 Т %? ) Т ‘

где N0 определяется по дисперсионной формуле (2.22′) или (2.22"), а Т0 и Р0 — соответствующие стандартные значения аб­солютной температуры и давления воздуха, при которых вы­числен N0.

Следует заметить, что эта формула не отвечает структуре N=NC+NB, т. е. первое и второе слагаемые в уравнении (2.24) не равны индексам преломления сухого воздуха и водяных па­ров соответственно, так как Р в первом слагаемом — это об­щее атмосферное, а не парциальное давление сухого воздуха. Последнее равно РС = Р—е, и формула (2.24), приведенная к виду N=NC+NB, должна быть записана следующим образом:

Продифференцировав дисперсионную формулу Коши по длине волны, а формулу Баррелла и Сирса по Т, Р и е, можно получить дифференциальные зависимости, выражающие влия­ние отдельных факторов на показатель преломления воздуха. Численные значения этих зависимостей при средних метеоро­логических условиях (Г=288 К, Р = 745 мм рт. ст., е=12 мм рт. ст.) и Я=0,632 991 мкм (длина волны гелий-неонового ла­зера в вакууме) будут следующими:

Полученные численные. значения производных позволяют легко решать задачи такого типа: найти, с какой ошибкой mN будет определен индекс преломления, если температура, дав­ление и влажность измерены с ошибками mT, тР и те. По­нятно, что

• <2-25>

Показатель преломления для радиоволн. Так как для ра­диоволн дисперсия практически равна нулю, показатель пре­ломления в каждой точке зависит только от метеорологических элементов Т, Р, е. Эта зависимость выражается формулой

N = o-p—f&+ (2.26)

В диапазоне дециметровых, сантиметровых и миллиметро­вых радиоволн XII Генеральная ассамблея Международного геодезического и геофизического союза (1960 г.) рекомендо­вала для коэффициентов о, b и с использовать значения, по­лученные Эссеном и Фрумом. Смит и Вейнтрауб на основании анализа данных различных авторов предложили несколько иные коэффициенты для формулы (2.26). В табл. 2 приведены

значения коэффициентов а, b и с по Фруму и Эссену и по Смиту и Вейнтраубу для случаев, когда Р и е выражены в миллиметрах ртутного столба (торах) и в миллибарах (гек­топаскалях) (760 мм рт. ст.= 1013,25 мбар; 1 мм рт. ст.« «1,33 мбар, 1 мбар«0,75 мм рт. ст.). Коэффициенты в табл. 2 даны в Л/’-единицах.

Формула (2.26), представленная в виде N = Nc + NBy записы­вается следующим образом:

N=a±f^+(a+b+f)T — (2,27)

Дифференцируя приведенные формулы по Т, Р и е, можно получить дифференциальные зависимости показателя прелом­ления от метеорологических элементов для радиоволн. Эти за­висимости при тех же, что и для света, средних условиях

АГ-ед/К;

N-eд/мм рт. ст.;

N-ед/мм рт. ст.

Сравнивая эти значения с соответствующими значениями для оптического диапазона, мы видим, что для радиоволн ве­личина dN/de более чем в 100 раз больше, чем для света. Это означает, что если влажность определена с ошибкой те, то вы-

3N

зываемая этим ошибка при вычислении N, равная ————- теу

де

в радиодиапазоне на два порядка больше, чем в оптическом диапазоне, что свидетельствует о важности точного определе­ния влажности воздуха при использовании радиоволн.

Проблема определения среднеинтегрального показателя преломления

Постановка задачи. Рассмотренные в предыдущем разделе формулы справедливы для каждой отдельной точки вдоль пути распространения волны. Реальная атмосфера — неоднородная

среда, в которой значения Г, Р, е меняются от точки к точке. Следовательно, показатель преломления, а значит, и скорость распространения волны будут меняться вдоль трассы.

Таким образом, в дальномерном уравнении

_ У*2Р 2

скорость v имеет неопределенность, так как v = v(x), где х — текущее значение расстояния. Какую же скорость нужно ис­пользовать при вычислении расстояния £>?

Логически очевидно, что в качестве скорости v должна фи­гурировать некоторая средняя скорость <v>—скорость, осредненная вдоль всего пути электромагнитной волны, а урав­нение для расстояния должно быть записано в виде

D _ (у)Чр (2.28)

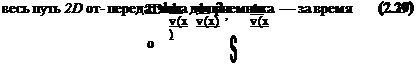Получим математическое выражение для этой средней скоро­сти. Электромагнитная волна проходит элементарный путь dx за время

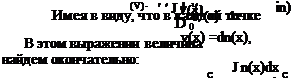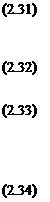Подставляя уравнение (2.30) в формулу (2.28) и решая по­следнее относительно <v>, получаем:

представляет собой среднеинтегральный (средний вдоль

трассы) показатель преломления воздуха, к определению ко­торого сводится задача о нахождении средней скорости <v>.

Методы определения <п>. Определение среднеинтеграль­ного показателя преломления — задача весьма непростая. Для строгого ее решения необходимо знать распределение метеоэле­ментов вдоль всей трассы распространения волны. Это распре­деление нам неизвестно — чтобы его знать, надо измерить тем­пературу, давление и влажность в каждой точке трассы или, во всяком случае, в достаточно большом количестве отдельных точек. Практически же измеряют метеоэлементы лишь в двух крайних точках — на концах линии; измерения даже в одной дополнительной точке где-то в середине трассы сопряжены с большими техническими и организационными трудностями, а в горных районах практически невозможны. Отметим, что распределение метеоэлементов на трассе луча может быть по­лучено, если организовать так называемое самолетное зондиро­вание атмосферы — полет оборудованного соответствующей ап­паратурой самолета (или вертолета) вдоль трассы. Несмотря на то что практически вряд ли можно обеспечить полет самолета точно по линии измерения, а также то, что само движение са­молета может вызывать локальные изменения метеопарамет­ров, этот способ в ряде случаев может дать неплохие резуль­таты. Однако понятно, что самолетное зондирование настолько громоздко, дорого и т. д., что если оно еще и может быть при­менено при работах научно-исследовательского характера, то совершенно неприемлемо при обычных дальномерных измере­ниях.

Все это приводит к тому, что среднеинтегральный показа­тель преломления может быть определен по измерениям метео­элементов лишь приближенно. Значение <п> приходится аппроксимировать значением, полученным из метеоизмерений в крайних точках линии. Если в начальной точке линии полу­чены значения Ти Ри еі, а в конечной — Г2, Р2, Є2, то в фор­мулу вида n=f(T, Ру е) подставляют средние значения:

гр _ 7*1 + Т2 . р _ Pi + Р% . с _ *1 + *я

2 ’ 2 ’ 2 ’

Иногда даже ограничиваются измерением метеоэлементов на одном конце линии (при длине линии примерно менее 5 км и превышении между концами линии примерно не более 100 м).

Такой способ определения показателя преломления прием­лем при измерениях не особенно высокой точности,’производи­мых дальномерами, инструментальная ошибка которых соизме­рима с ошибкой, возникающей из-за указанной приближенности определения среднеинтегрального показателя преломления.

Для повышения точности определения среднеинтегрального показателя преломления (при метеоизмерениях на концах линии) стремятся измерять линию дальномером при различных метеоусловиях, для чего приходится «растягивать» измерения, выполняя их в различное время суток. Основанием к такому методическому приему служит то обстоятельство, что, по­скольку при изменении метеоусловий меняется неизвестное нам распределение метеоэлементов на трассе, значение показа­теля преломления, выведенное по измерениям метеоэлементов на концах линии и осредненное по различным метеоусловиям, будет с большей вероятностью приближаться к среднеинтег­ральному значению, чем при неизменной метеорологической си­туации.

Указанный прием несколько повышает точность, но не дает радикального решения задачи, ибо не устраняет приближен­ность определения <п>.

При измерениях, производимых дальномерами высокой ин­струментальной точности, приближенность определения сред­неинтегрального показателя преломления может существенно влиять на точность измерения расстояния. Именно это влияние в настоящее время ограничивает повышение точности дально — мерных измерений. Поэтому проблема более точного определе­ния <п> является одной из важнейших задач современной геодезической дальнометрии.

Светодальномеры, как правило, обеспечивают более высо­кую точность измерений, чем радиодальномеры, так как изме­рения в оптическом диапазоне свободны от ошибок из-за отра­жений от подстилающей поверхности и требуют менее точного учета влияния влажности. Поэтому проблема определения среднеинтегрального показателя преломления воздуха встает в первую очередь при высокоточной светодальнометрии. Эта проблема может быть решена применением так называемого дисперсионного метода, обеспечивающего возможность аппара­турного (инструментального) определения среднего вдоль трассы показателя преломления. Аппаратурное определение величины <п> при измерении расстояний принято называть дальномерной рефрактометрией.

Комментарии запрещены.