Бурение грунтовых зондов, установка энергетических колодцев

Так же как и при рассмотрении кинематики долота, колон­ну бурильных труб можно моделировать различными схемами, используемыми при решении разных конкретных задач. В наи­более общем виде колонна представляет собой сложную систе­му, включающую в себя бурильные трубы с замками, различные по сечению и по материалу, из которого они изготовлены. В эту систему могут входить также забойный двигател:, различные переводники, амортизаторы, центраторы, расширители и другие устройства, предназначенные для обеспечения процесса буре­ния с заданными технологическими показателями. Некоторые варианты компоновок колонны будут нами рассмотрены ниже. Однако исходить лучше всего из простейшей схемы, в которой колонна моделируется длинным стержнем постоянного сечения, что соответствует простейшему варианту роторного бурения без УБТ. Учет наличия замковых соединений не вносит сколько-ни­будь заметных изменений в получаемые результаты по сравне­нию с расчетом колонны постоянного сечения. Это было показа­но Р. Бредбери и Д. Уилхойтом [9].

Затухающие продольные колебания гладкого стержня или трубы постоянного сечения описываются гиперболическим диф­ференциальным уравнением

д2и(х, t) , « ди(х, t) , — „д2и(х, t) /п

+ g = а2 v ’ ; , 2.16)

at* dt дх2

где и(х, t)—перемещение точки колонны с координатой х в момент времени t; Я = р/рЛ— коэффициент затухания; ц — коэф­фициент демпфирования; А — площадь поперечного сечения ко­

лонны; р — плотность материала труб; а — скорость распрост­ранения продольной волны; g—ускорение свободного падения.

Примем, что в начальный момент времени колонна буриль­ных труб находится в растянуто-сжатом состоянии, опираясь на забой с силой, соответствующей нагрузке на долото G. Нетруд­но получить распределение напряжений в такой колонне.

г — d’i — G /п, _

<2Л7>

где у — удельный вес материала труб.

Интегрируя уравнение (2.17), получаем

и = —— х2 — х + С,

2 Е АЕ

где С — постоянная интегрирования.

Приняв, что перемещения на верхнем конце колонны при х=Ь равны нулю u/x=L=0, получим

и=^-х2 —х — . (2.18)

2 Е 2 Е 2 Е АЕ х ‘

Выражение (2.18) описывает распределение перемещений и по колонне в начальный момент времени и, следовательно, яв­ляется начальным условием для решения уравнения (2.16).

Другим начальным условием является равенство скоростей сечений колонны нулю в момент времени t=0.

Граничные условия уравнения (2.16) определяются силой со­противления породы внедрению зубцов долота и, как было при­нято выше, равенством нулю перемещений верхнего конца колонны.

Таким образом, краевые условия для решения уравнения продольных колебаний колонны бурильных труб можно запи­сать в следующем виде

/ I V 2 6 yL2 . GL

и (х, t) о = —— х2 х 1 Ь — г—.’

v ’ п 2Е АЕ 2Е АЕ

ди (х, t) dt ди (х, t)

= 0;

(2.19)

t=о

_ Р (0 .

х=0 АЕ ’

дх

U (X, t) x=l = О,

где P(t) —суммарная сила сопротивления породы внедрению всех контактирующих зубцов долота, приложенная к нижнему сечению колонны [см. формулу (2.14)]; Е — модуль упругости материала труб.

Заметим, что краевые условия могут быть выбраны и иными. Например, колонна может быть принята полностью растяну­той, свободно висящей на крюке, а долото ненагруженным

и т. д. Однако произвольный выбор граничных условий не от­ражается на результатах расчета установившегося процесса бурения.

Уравнение (2.18) является гиперболическим дифференциаль­ным уравнением второго порядка в частных производных, для которого определены начальные и граничные условия. Краевые условия таковы, что область аргументов, в которой должна быть найдена функция и(х, t) остается открытой в направле­нии переменной t.

Сложность решения задачи заключается в том, что гранич­ные условия на нижнем конце колонны бурильных труб опре­деляются нелинейной функцией P(t) =’LP[z(t)]. Здесь име­ется в виду суммирование сил сопротивления для всех контак­тирующих зубцов долота, которые для каждого момента вре­мени находятся через соответствующие углубления зубцов в породу. Поэтому будем искать приближенное решение задачи путем замены дифференциального уравнения и его краевых ус­ловий соответствующими разностными соотношениями.

При решении уравнения (2.16) используется явный метод сеток, когда решение в точках области определения уравнения подсчитывается шаг за шагом, исходя из граничных и началь­ных условий. Итак, требуется найти решение одномерного вол­нового уравнения продольных колебаний колонны бурильных труб в области Q{Os£x=SL, t>-0}.

Построим сеточную область и перейдем к составлению со­ответствующей разностной задачи.

Для лучшей сходимости решения разностной краевой задачи с решением одномерной волновой задачи необходимо, чтобы выбор сетки подчинялся условию [11] aAt = Ах, где At — шаг по времени; Ах — шаг по оси х.

В области определения Q{0^x<L, t>0} дифференциально­го уравнения продольных колебаний колонны труб проводим два семейства параллельных прямых:

х = iAx; t = jAt,

где i = 0, 1, …, п; j = 0, 1, …, m, …

Тогда шаг по оси х определится как Ax=L/n, а по оси у — согласно приведенному выше условию лучшей сходимости А/= = Ах/а. Область определения £2 покроется прямоугольниками, вершины которых принято называть узлами сетки. Суть приме­няемого метода заключается в том, чтобы для произвольного узла сетки найти значение функции и(х, t) по ее значениям в нескольких соседних узлах. Для каждого внутреннего узла сет­ки (г, /) составим разностное уравнение, аппроксимирующее в этом узле дифференциальное уравнение. Производные заменяем разностными соотношениями

ди ui+i. j иЧ. ди _ ui. j+1 uij.

дх Ах ’ dt At ’

TOC o "1-5" h z *5×2 Дх2 d/3 At* ‘

(2.20)

Разностное соотношение подставим в волновое уравнение

(2.16)

«,./+,-2ад, + , мг-./+1-м£/ и,+1./-2и„ + ./

—————————- — J — Д——————- Г Л — и •

At* At Ах*

(2.21)

Так как Д/ = Дх/а, то уравнение (2.21) примет вид

uc. i+i 2Mo~“Mt./-fi, о “f./+i ич’ , 2 —2uci~^uc—

—————————— /, 1————————- 0 = a : i

At* ‘ Д< 16 Дх*

После элементарных преобразований получим

XAtUil U; ; , + U; , , ,• + U; , ; ДД/2

Ut,+1=——- ^1+1 ■’ 1~и> . (2.22)

1+Ш ’

где i=l, 2, …, п —1; /=1, 2, …

Из формулы (2.22) следует, что, зная значение решения в узлах вертикальных слоев t = Atj и t — At(j—1), можно найти ре­шение во всех внутренних узлах слоя

t = At (j +1).

Для того чтобы найти приближенное решение нашей краевой задачи, необходимо знать значение решения на двух начальных слоях ^ = 0 и t = At и уметь определить значения на границах области определения уравнения, т. е. при х = 0 и x = L.

Из начального условия (2.19) следует, что на первом слое / = 0 значения перемещений могут быть вычислены по формуле

= TF (Д*г)* — Ж 4*г ~ + 7?’ <2’23>

где / = 0, 1, …, п.

Прежде чем перейти ко второму слою t = At, выведем фор­мулу для расчета перемещений в узлах сетки, находящихся на границах области определения дифференциального уравнения. Для этого введем дополнительные фиктивные слои сетки х = = —Дх и t = —At. Уравнение (2.22) применим к нижнему концу колонны, т. е. для слоя х = 0,

• Ши0/ — «0 /_, + ы1;- + и_ч — gAt*

№.,•+, = .

Значение перемещений u_i. j в точках фиктивного слоя сетки х = —Дх нетрудно получить из граничного условия (2.19) для х = 0

Отсюда

р Vi)

u—j — u0j -)—Дх

или

• Р(^ a +

Ы—1/ = Щ] -1- a At.

Подставив значение «_ij в уравнение (2.24), получим форму­лу для вычисления перемещений нижнего сечения колонны бу­рильных труб

* р Vi) ,

а^ АЕ + (1 + «о/ — «о /-1 + иИ — 8At2

=———— ms;——- <2-25)

для /> 1.

Запишем уравнение (2.25) для слоя f = M

^ (//)

(2.26)

аА/ Д4£~ + ^ + Ш) и°° ~uo.-i+ui. o — 8&t2 1 + Ш

Для определения фиктивной величины щ. — i используем одно из начальных условий (2.19)

ди uio ui— 1 ~

(2.27)

~дГ ~ At ~ ’ ill.—i и0.—i «оо*

Следовательно, формула (2.26) примет вид

PV о)

АЕ

aAt аf° + (1 + Ш) ы00 — «оо + ы,-0— gAt*

U01 —

1 +Ш или

аД* —j—■ — f lAtu00 + «1 0 — gA/2

«ох =————— г——————- •———— (2-28)

1 + %At

Для определения перемещений в остальных точках верти­кального слоя At воспользуемся формулой (2.22). Распишем ее для вертикального слоя At

и _ ~ 0 и(о + ис+1 .о — г ut-1 .о — SAt8

11 l-j-Ш I • /

для i=l, 2, …, п —1.

Перемещения в узловых точках горизонтального слоя сетки х = пДх для верхнего сечения колонны x=L находим, используя одно из краевых условий (2.19) дифференциального уравнения

(2.16)

«п./= 0 для / = 0,1, . . , (2.30)

Учитывая выведенные формулы, можем рассчитать значение перемещений и (х, t) в любом внутреннем и находящемся на границе области определения П { Os^x^L, t^O [ узле сетки

мя i = 0’1′ • •

или

(Ш — 1) Mj-o + ы(.+1 .0 —gA/2 .

ип =——————— ;—————————— для 1 = 1, 2, . . . ,Я— 1;

1 + лД*

Р (*/)

аД*~Л£ + (1 + Ш) и0/ —и0 /_!+«!/—gAf*

«о. ж =———————— Г+ш———————— ^ ^ 1; (2>31)

Шщ, +«[.+к/ + и._, §д/а

=———————- ГТЩ——————- для ‘ ” 12, • ■

. . . , п— 1;

Mrt./+i = 0 для / > 0.

По формулам (2.31) можем последовательно находить ве­личины продольных перемещений на любом горизонтальном слое по их значениям на двух предыдущих слоях.

Решение составленной нами разностной краевой задачи сво­дится при выбранном соотношении шагов сетки к решению краевой задачи для одномерного волнового уравнения (2.16), причем величина погрешности метода не превосходит Дх2. Сле­довательно, точность решения данного уравнения зависит от выбора масштаба разбивки по оси х, что определяет, как выяснено выше, и шаг по времени At.

При решении ряда задач с целью упрощения вычислений це­лесообразно преобразовать волновое уравнение колебаний ко­лонны (2.16). Для этого полную величину перемещения каждо­го сечения и (х, t) разделим на две аддитивные составляющие [17], которые условно назовем динамической v(x, t) и стати­ческой w(x). В этом случае

и (х, t) = v (х, t) +w (х). (2.32)

TOC o "1-5" h z о d2w (х) . п

а —ГГ +2=°’

/О QQ

d2v(x, t) ^ dv (х, t) _ q2 дгУ (х, t) ‘ ‘ ‘

dt2 dt дх2 ‘ .

Решение первого уравнения этой системы дает статическое распределение перемещений вдоль колонны, уже вычисленное выше, (2.18).

При исследовании динамических составляющих перемеще­ний колонны можно рассматривать только второе уравнение системы (2.33)

а*° (*’ о I у ди (*. о — п2d2v (*. о,234v

а/2 а/ дх2 ’ у

При решении этого уравнения статические перемещения, вы­зываемые весом колонны, можно принять равными нулю. Соот­ветствующие краевые условия для решения (2.34) запишутся в виде

v (х, t) |*=о = 0; дУ (х, t) | _ q

dv (х, 0 I Р (0 — G. (2.35)

dx |дс=о АЕ ’

v (X, t) X=L = 0.

Как видим, граничные условия на нижнем конце колонны включают вместо силы сопротивления породы P(t) величину [Я(/)—G]. Это необходимо, так как в противном случае не мо­жет быть удовлетворено начальное условие v(x, ^)|<=0 = 0. Фи­зический смысл учета нагрузки заключается в том, что при исключении статических деформаций рассматриваются дина­мические колебания, вызванные разностью сопротивления по­роды и нагрузки на долото.

Решение уравнения (2.34) с краевыми условиями (2.35) принципиально ничем не отличается от решения уравнения

(2.16) и также выполняется методом сеток.

При решении конкретных задач встречаются практически

важные случаи, когда может быть осуществлено дальнейшее

упрощение волнового уравнения так, что решение его может быть получено в квадратурах. Например, если рассматривать динамические перемещения сечений настолько длинной колон­ны бурильных труб, что можно пренебречь влиянием отра­женных волн и не учитывать затухания амплитуды продольных колебаний в ее нижней исследуемой части, то порядок уравне­ния может быть понижен.

Тогда уравнение продольных перемещений колонны и соот­ветствующие краевые условия могут быть записаны в виде

dv(x, i) = а ди (х, t) . dt дх ‘

ди (х, t) Р (t) — G. (2-36)

дх х=0 АЕ ’

v (х, t) |<=0 = о.

Перемещения нижнего сечения колонны бурильных труб мо­гут быть рассчитаны по следующей разностной формуле:

Р {tA — G

V0.J+1 = voj + —^ аМ. (2.37)

Выше были рассмотрены некоторые варианты волнового уравнения продольных колебаний колонны бурильных труб по­стоянного сечения.

Кроме продольных колебаний наиболее существенным обра­зом, определяющих эффект взаимодействия долота с породой, в колонне могут возбуждаться и другие виды колебаний, на­пример крутильные и поперечные. Заметим, что разные виды колебаний могут оказывать друг на друга взаимное влияние. Ограничимся здесь кратким рассмотрением процесса крутиль­ных колебаний, возникновение которых связано с самим процес­сом разрушения горных пород долотом в забое.

Прежде чем начать рассматривать процесс крутильных ко­лебаний, необходимо дать пояснения относительно понятия крутящего момента. Под крутящим моментом понимают мо­мент, необходимый для поддержания заданной угловой скоро­сти вращающейся системы. Очевидно, что понятие это неравно­значно для роторного бурения и бурения с забойным двигателем, ибо в последнем случае под крутящим моментом понимается только момент, необходимый для вращения долота.

Этот последний складывается из суммы моментов, необходи­мых для преодоления сопродавления жидкости вращению доло­та и переводника, трения во вращающихся элементах долота как механизма и, наконец, момента перекатывания долота по забою.

При моделировании бурового процесса можно непосредст­венно вычислять только момент перекатывания, как функцию времени. Однако важной динамической характеристикой рабо­ты долота является полный потребный крутящий момент. Его можно определить как сумму среднего по времени момента пе­рекатывания, момента трения в опорах долота и момента тре­ния системы, вращающейся в промывочной жидкости. Для определения моментов трения можно воспользоваться имею­щимися экспериментальными работами. В качестве примера приведем работу С. Г. Бабаева и И. А. Даниеляна [6], данные которой позволяют сделать оценку моментов трения для неко­торых серийно выпускаемых долот.

Моменты трения в опорах по закону, близкому к линейному, зависят от осевой нагрузки и возрастают так же, по­степенно выполаживаясь, с увеличением скорости враще­ния. Кроме того, момент трения в опоре долота не­значительно увеличивается при переходе с воды на глинистый раствор. По мере износа опор момент тре­ния также линейно возрастает. Таким образом, для каждого момента трения и для выбранного режима бурения величина мо­мента в опорах может быть приблизительно определена.

Что касается момента, затрачиваемого на трение о стенки скважины и промывочную жидкость, то и здесь может быть сделана количественная оценка на основе имеющихся экспери­ментальных данных [15]. Естественно, что эта составляющая крутящего момента зависит главным образом от скорости вра* щения долота.

Общая величина крутящего момента, необходимого для преодоления различных сил трения, препятствующих враще­нию, колеблется в широких пределах и в сумме может дости­гать 100 кгс*м и более. Такой момент вполне соизмерим, а иногда и превосходит крутящий момент перекатывания.

Разумеется, экспериментальные материалы, связанные с определением моментов, трения, должны систематически обнов­ляться в связи с совершенствованием конструкции опор буровых долот, а также составов промывочных растворов.

При дальнейшем изложении главным образом будем рас­сматривать момент, необходимый для разрушения породы на забое скважины, и для удобства будем называть его просто крутящим моментом и обозначать через М. Среднее по време­ни значение Л1Ср.

1 ‘

MeJ> = —$M(f)dt. (2.38)

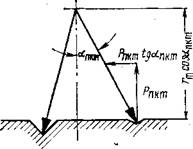
Рис. 13. Схема к расчету крутя­щего момента

Осреднение проводится в процессе вычислений крутяще­го момента M{t) за период времени, в течение которою должно произойти не менее одного полного цикла контакта зубца долота с забоем.

Текущая величина крутя­щего момента зависит от зна­чения силы сопротивления по­роды внедрению зубцов долота в данный момент P[znkm (t)] и положения центров шарошек относительно контактирующих зубцов. Очевидно, что полный
крутящий момент образуется как сумма моментов перекатыва­ния относительно всех контактирующих зубцов.

Из рис. 13 следует, что

Мякт (t) = rkmP [znkm (/)] sin ankm (t). (2.39>

Полный крутящий момент M (t) на долоте определяем сле­дующим образом

M(t)= 2 rkmP [znkm (/)] sin ankm (t). (2.40>

nkm

Вполне очевидно, что для вычисления M(t) и Мср достаточ­но пользоваться расчетной схемой продольных колебаний доло­та и колонны. Поэтому величина Мср определяется еще до на­чала рассмотрения крутильных колебаний и используется для: составления краевых условий. При дальнейшем совместном рас­чете двух видов колебаний системы произойдет автоматическая коррекция величин углубления зубцов, функции поворота ша­рошек от времени и появится новое, уточненное значение сред­него крутящего момента с учетом влияния крутильных коле­баний.

При крутильных колебаниях цилиндрического стержня каж­дое сечение остается в своей плоскости и поворачивается отно­сительно центра симметрии. Обозначим угол поворота сечения относительно его центра через 0(х, t). Тогда уравнение крутиль­ных колебаний запишется в следующем виде:

d29(x, t) . g 99 (х, t) _ачдЩ(х, /) (2 41У*

dt2 dt 1 дх2 ’

где | — коэффициент затухания; ai=y/~i/p — скорость распро­странения волны сдвиговых деформаций; р — модуль сдвига материала труб.

Будем считать, что в начальный момент рассмотрения про­цесса (/=0) колонна бурильных труб имеет некоторое стати­ческое распределение угла закручивания, обусловленное дейст­вием среднего по времени крутящего момента,

в(х)=^-, (2.42)»

Р7р

где /р — полярный момент инерции сечения труб.

Это выражение является, естественно, начальным условием: для решения уравнения (2.41).

Другим начальным условием может быть принято равенство нулю угловых скоростей сечений колонны в момент времени ^=0. Само собой разумеется, что угловая скорость вращения колонны в целом со считается постоянной и при расчете крутиль­ных колебаний не учитывается.

Граничные условия для решения уравнения (2.41) опреде­ляются наличием момента. необходимого для вращения

долота. На верхнем конце колонны можно принять постоянным угол закручивания, определяемый средним крутящим моментом.

(2.43)

В целом краевые условия для решения уравнения кру­тильных колебаний колонны бурильных труб можно записать следующим образом:

0 (х, t) |,=0 — 59 (х, t) = 0; dt t=0 59 (х t) M{t) . дх x=0 pip ’ 0 (х, P/p

Вполне аналогично случаю продольных колебаний можно принять, что углы скручивания сечений в начальный момент времени равны нулю, т. е. учитывать только их динамические составляющие. В этом случае общий вид волнового уравнения де изменится, так как на процесс крутильных колебаний ника­кие массовые силы не действуют. Разница будет заключаться только в краевых условиях. Роль осевой нагрузки при этом •будет играть средний крутящий момент Мср, так что разница „M(t)—Мср будет являться источником динамической составля­ющей крутильных колебаний нижнего сечения колонны.

На основании изложенного, краевые условия для решения уравнения (2.41) можно записать в виде

TOC o "1-5" h z 0 (х, t) |f=0 = 0; d9 (s, t) q.

t=0 ’ /о ^

59 (x, f) f M (Q — Mcp. ‘ 44’

dx x=o [ilp

0 (x, t) x—L = 0-

Как видим, в этой схеме динамическая составляющая кру­тильных колебаний верхнего сечения колонны труб принята равной нулю.

Схема решения волнового уравнения крутильных колебаний колонны бурильных труб полностью идентична изложенной выше схеме решения уравнения продольных колебаний.

Представленная выше методика решения дифференциаль — дых уравнений продольных и крутильных колебаний колонны позволяет рассчитать перемещения и углы закручивания сече­ний колонны в любой момент времени t, если в этот момент времени будут известны углы поворота шарошек, углубление каждого контактирующего с породой зубца, сопротивление по­

роды этим углублениям и изменение потребного крутящего момента на долоте, ибо эти величины определяют граничные условия решаемых волновых уравнений.

Очевидно, что процессы продольных и крутильных колеба­ний, как уже указывалось выше, взаимосвязаны. В рассматри­ваемой модели связь эта реализуется через изменения скоро­сти вращения нижнего сечения колонны при наличии крутиль­ных колебаний. При расчете углов поворота шарошек измене­ние скорости dca/dt может быть учтено в каждый момент вре­мени. Таким образом, уравнения продольных и крутильных ко­лебаний будут решаться совместно, что позволяет учесть влия­ние крутильных колебаний на процесс разрушения породы и формирования забоя.

Следует иметь в виду, что в определенных случаях, кроме продольных и крутильных колебаний колонны, может играть заметную роль и процесс поперечных колебаний, источником которых, в частности, являются несбалансированные вращаю­щиеся массы забойного двигателя. В настоящей книге этот вопрос не рассматривается.

Комментарии запрещены.