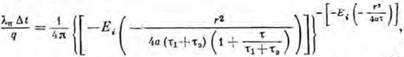Бурение грунтовых зондов, установка энергетических колодцев

Поскольку определять геотермический градиент и некоторые другие геотермические параметры можно в условиях практически установившегося режима, необходимо установить время нагревания
или остывания скважины, заполненной жидкостью с температурой, отличной от температуры окружающих ее пород. Решение этой за­дачи позволит замерять температуру пород в скважинах с пеуста — новивпгамся тепловым режимом, если найдена разница температур жидкости и породы. Кроме того, это необходимо для определения характера изменения температуры в бурящейся скважине после прекращения в пей циркуляции.

Решить задачи, связанные с изучением естественных и особенно искусственных тепловых полей, довольно трудно вследствие слож­ности протекания процесса теплообмена в скважине.

Время, в течение которого в скважипе восстанавливается тепло­вой режим, обычно определяют экспериментально.

Так, температуру замеряют через 5—10 суток [81 после бурения. Иногда время нахождения скважипы в покое доводят до 2—3 меся­цев и более [831. Анализ материалов термических исследований сква­жин Сибири [831 и Молдавской ССР показал, что термический ре­жим полностью восстанавливается более чем через 50 суток. Для скважин, пробуренных в толще многолетней мерзлоты, время вос­становления термического режима возрастает от одного года до двух лет и более.

В работе [8] сделана попытка установить зависимость геотерми­ческих ступеней, наблюдаемых в охлажденных при бурении сква­жинах, от времени, прошедшего после окончания циркуляции про­мывочного раствора. Было установлено, что величины этих ступеней изменяются от 39 до 140 мГС независимо от времени покоя.

Решепие вопросов, относящихся к термическому режиму земной коры, затруднено тем, что сведения о характере распространения радиоактивных элементов, изменении их концентрации с глубиной и во времени неточны, отсутствуют данные об изменении теплопро­водности и других физико-тепловых свойств пород с глубиной и т. п. Все это приводит к тому, что многие теоретические задачи геотермии решаются при наличии значительных допущений, поэтому носят приближенный характер.

Так, при рассмотрении задачи об остывании (или нагревании) скважины, заполненной какой-либо жидкостью, имеющей темпера­туру, отличную от температуры пород, принимается, что характер остывания скважипы аналогичен до известной степени остыванию цилиндра бесконечной длины.

Тепловое поле в рассматриваемом случае будет иметь аксиаль­ную симметрию и, кроме того, не будет зависеть от переменной Z, поскольку изменение температур по длине скважины в пределах изучаемых пластов незначительно.

В результате такой предпосылки дифференциальное уравнение теплопроводности в цилиндрической системе координат (1.3а) при­нимает вид:

(IV.19)

и его решение при условии, что все исследуемое пространство, вклю­чая скважину, однородно и изотропно, приводит к выражению

A*—A/0(l—е"5^). (IV.20)

где At0 и At — соответственно начальная и конечная разности температур окружающей среды и жидкости по истечении времени т; г0 — радиус скважины; а — температуропроводность бурового рас­твора, равная температуропроводности пород.

Экспериментальные исследования, проведенные Н. К. Куха- ренко и Г. А. Череменским [85], показывают, что в общем характер изменения опытных и теоретических кривых, рассчитанных по фор­муле (IV.20), совпадает, но при экспериментальных исследованиях процесс изменения температуры пород протекает более медленно.

Аналогичная задача при условии, что температуропроводность глинистого раствора отл1гчна от температуропроводности пород, решена А. И. Заборовским, по имеет весьма сложное и громоздкое

решение, которое здесь не приводится. Кривые / (т), по­строенные но формуле А. И. Заборовского, указывают на различ­ный характер остывания глинистого раствора в зависимости от тепловых свойств пород. Однако, как следует из работы P. JI. Сол — ганика и В. Н. Дахнова, использование зависимости А. И. Забо­ровского может привести к ошибочным результатам.

В работах А. И. Заборовского, В. Н. Дахнова и Д. И. Дьяко­нова при выводе приведенных выше зависимостей не учитывается зона нарушения термического режима, образующаяся вокруг сква­жины.

С учетом зоны нарушения термического режима пластов Г. А. Череменский [851 предложил зависимость для определения времени простоя скважины до наступления установившегося тепло­вого режима

(IV.21)

где — Е( ^ — экспоненциальный интеграл; г — радиус сква­

жины; а — температуропроводность пород и промывочного раствора; Tj — время нарушения термического режима; т — время простоя

скважины; т, — время ^для пспронпцаемых пород равно

коэффициент теплопроводности пород; q — количество тепла, отда­ваемого промывочным раствором породам на единице длины сква­жины в единицу времени; At — разница температур пород и глини­стого раствора по истечении времени т.

На основе зависимости (IV.21) были построены кривые ХПЛt/q — — / (т), которые затем были совмещены с точками эксперименталь­ных наблюдений по скважинам Аляски и Колпашева. При этом экс­периментальные и теоретические кривые полностью совпали.

Таким образом, в работе А. Г. Череменского (85] докааано, что восстановление теплового режима при простое скважины подчи­няется зависимости (IV.21). Поэтому, решая уравнение (IV.21) относительно т или At, можно определить время, необходимое для восстановления нарушенного теплового режима скважины пли же перепад температур жидкости и пласта в любой момент простоя скважины при отсутствии циркуляции в ней.

Однако определение многих величин, входящих в зависимость (IV.21), в условиях скважины представляет сложную и нерешенную задачу. Поэтому практическое применение формулы (IV.21) до из­вестной степени ограничивается.

То же относится и к эмпирической формуле, предложенной Т. К. Меликовым для определения температуры пласта по измеренной температуре в скважине:

fB = fT(l + in^±lL), (IV.22)

где <п — истинная пластовая температура; tT — температура, за­меренная в скважине; Tt — продолжительность циркуляции про­мывочной жидкости в ч; х2 — время, прошедшее после окончания циркуляции до замера температур, в ч.

Очевидно, время простоя скважипы для восстановления нарушен­ного промывкой теплового состояния пород неодинаково для различ­ных участков скважины.

Так, в скважине всегда есть точка, в которой температура пород и жидкости одинакова. Выше этой точки температура пород меньше температуры промывочной жидкости, а ниже — больше этой темпе­ратуры. Спустив термометр на глубину этой точки, можно в любое время замерить истинную температуру пород; методика этого замера известна. Выше и ниже этой точки должно быть соблюдено то или иное время, в течение которого жидкость в скважине воспримет температуру окружающих пород. Например, в работе [95] показано, что быстрее всего температурное равновесие восстанавливается у за­боя скважины.

Автор работы (98) доказывает, что минимальное время устано­вления теплового равновесия наблюдается у пористых пород в скважинах с вевязким раствором.

В заключение отметим, что экспериментально процесс восстано­вления температур при простое бурящейся скважины, заполненной глинистым раствором, еще не изучался.

Комментарии запрещены.