Бурение грунтовых зондов, установка энергетических колодцев

(2.14)

Построенная выше модель процесса работы шарошечного. долота при глубоком бурении требует определения для любого момента времени t суммарной величины силы сопротивления породы Р при ее взаимодействии со всеми контактирующими зубцами, т. е.

P{t) = >] PUnkm(t)].

nkm

Как видно из этого соотношения, суммированию подвер­гаются зависимости Piznkm(t) для каждого зубца с учетом его углубления в данный момент времени. Уравнение кинематики долота определяет взаимное расположение зубцов всех венцов шарошек относительно забоя, и, следовательно, величины ■Znkm(t) могут быть вычислены.

Поэтому задача сводится к определению функций P(z) для зубцов разной формы и конфигурации. При этом должны быть учтены условия залегания породы при бурении глубоких сква­жин, а также динамический характер взаимодействия зубцов с породой.

Чтобы разобраться в характере и физическом смысле зави­симости Р(г), необходимо привести вкратце основные сведе­ния о механизме разрушения горных пород.

Как показывают экспериментальные исследования, процесс разрушения горной породы включает три стадии:

— упругая деформация;

— остаточная деформация;

—отделение части породы от массива.

Упругая стадия взаимодействия зубца долота с породой определяется только краевыми условиями задачи — формой; площадки контакта и эпюрой давления по этой площадке, а также коэффициентом Пуассона горной породы. Расчет на­пряженного состояния породы для контактных площадок раз­личной формы [35] и последующий прочностной анализ полу­пространства [3] позволили построить теоретически общую схему возникновения и развития процесса разрушения после выхода породы из упругого состояния. Из анализа следует, что разрушение должно начаться в зоне контура контактной пло­щадки при сравнительно малой нагрузке на зубец. Оно должно иметь характер хрупкого отрыва в площадках, перпендикуляр-^ ных к свободной поверхности полупространства. В результате на поверхности должна образоваться кольцевая трещина от­рыва, охватывающая контактную площадку. Предполагая, чтс дальнейшее развитие трещины будет происходить вдоль траек­тории главных нормальных растягивающих напряжений, начи­нающейся на свободной поверхности из кольцевой трещины, можно заключить, что она будет иметь вид расходящегося ко­нуса, кругового или эллиптического. Экспериментальная про­верка этой гипотезы вполне подтвердила ее для группы горных пород, таких, как кварцит, доломиты, песчаники, некоторые известняки и другие.

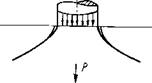
Коническая трещина разделяет верхнюю часть полупрост­ранства на две области: усеченный конус и окружающую era консоль. Заключительная стадия процесса разрушения состоит в отломе консоли путем передачи на нее части давления штам­па через материал конуса. Отлому консоли предшествует пол­ное или частичное разрушение материала конуса, приводящее к увеличению доли внешнего давления, передаваемого на кок — соль. Это давление со стороны конуса приводит к изгибу кон­соли и появлению на внутренней поверхности растягивающих напряжений, под действием которых образуется трещина от­рыва, чаще всего нормальная к конической трещине и выходя­щая на поверхность полупространства под малыми углами к последней (рис. (■>,</)

Описанный процесс разрушения горных пород называется первым механизмом разрушения. Как показывают экспери­менты, в ряде пород первый механизм разрушения или совсем не развивается или, начав развиваться, затухает, и дальнейшее разрушение происходит по так называемому второму меха­низму.

Причина, приводящая к тому, что коническая трещина не развивается, заключается в том, что на контуре площадки кон­такта растягивающие напряжения в некоторых породах вместо того, чтобы увеличиваться с ростом давления на зубец, начи­нают уменьшаться из-за увеличения объема сжатой породы непосредственно под площадкой контакта. Типичным предста-

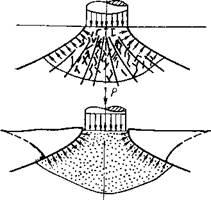
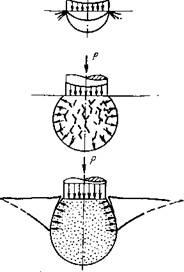
Ряс. 6. Первый а и второй б механизмы разрушения горных пород

вителем таких материалов является мрамор. При. наличии дифференциального давления на поверхности забоя по второму механизму могут разрушаться те породы, которые в атмосфер­ных условиях разрушаются по первому.

Суть второго механизма заключается в следующем. По мере увеличения нагрузки на зубец под площадкой контакта разви­вается зона необратимых деформаций (пластические деформа­ции и микротрещиноватость зерен, потеря связности между ними и т. д.). При малых нагрузках зона необратимых дефор­маций, или зона предразрушения, локализуется в окрестностях контура площадки, а по мере роста нагрузки развивается! в глубь массива, принимая в конце концов форму усеченного овального ядра. Какова бы ни была физическая природа струк­турных изменений в этом ядре, результатом является то, что полупространство, как и при первом механизме разрушения, разделяется на две части: предразрушенное ядро и окружаю­щую его упругую консоль. _

Заключительная стадия процесса разрушения аналогична случаю первого механизма. По мере накопления структурных изменений в материале ядра, он начинает передавать давление зубца на консоль в возрастающей степени, в результате чего
консоль отламывается и первый скачок процесса разрушения завершается (рис. 6,6).

На основании описания механизмов разрушения нетрудно заключить, что характеристика этого процесса P(z) для пер­вого скачка разрушения должна состоять из трех участков: упругого линейного участка, нелинейного возрастающего уча­стка, соответствующего необратимой деформации конуса, или ядра предразрушения, и участка резкого уменьшения силы, соответствующего отлому консоли.

Возникновение и развитие конической трещины при первом механизме разрушения не изменяет упругого характера полу­пространства в целом и поэтому не должно существенно влиять на ход кривой P(z). После образования трещины сопротивле­ние породы внедрению зубца несколько уменьшится и линей­ный участок кривой может незначительно изменить угол на­клона. При дальнейшем внедрении зубца в породу после отлома консоли весь процесс должен качественно повторяться, образуя второй и последующие скачки разрушения. Очевидно, что максимальное значение силы в каждом последующем скачке должно в принципе возрастать, так как разрушение по­роды в углублении требует большей силы, чем на плоской поверхности. При достаточно быстром и непрерывном внедре­нии зубца уменьшение силы на падающих участках может быть незначительно.

При наличии дифференциального давления внешнее давле­ние на консоль препятствует ее выходу, что приводит к суще­ственному увеличению максимальных нагрузок, необходимых для реализации каждого скачка. Кроме того, давление, удер­живающее консоль от выкола, препятствует уменьшению на­грузки между скачками. В результате этого скачкообразный характер зависимости P(z) должен существенно сглаживаться.

Поскольку в практике удельные давления на зубец могут оказаться недостаточными, вполне возможно, что будет реали­зована только часть характеристики P(z), иногда даже непол­ный первый скачок. В этом случае принято говорить о так называемом усталостном разрушении горной породы.

На основе знания деталей механизмов разрушения можно* попытаться оценить возможность теоретического описания функций P(z), используя для каждого из ее участков соответ­ствующие уравнения механики.

Решение классических задач теории упругости позволяет нам рассчитать функцию P(z) для первой стадии, т. е. опреде­лить ее при упругом прогибе породы. Для этого нужно опре­делить упругое опускание полупространства от действия штампа, соответствующего конфигурации эталонного зубца. Так, например, для сферического жесткого штампа зависимость, величины упругого прогиба породы 2 от действующей нагруз­ки Р имеет следующий вид [10]:

1 13/9я(1-у«) pf

2 / 2р Е ’

где v — коэффициент Пуассона; р — радиус скругления вер­шины штампа; Е — модуль упругости породы.

Аналогичные зависимости упругого прогиба г полупрост­ранства от нагрузки Р в случае прямоугольного штампа могут быть взяты из работ А. Лява [47] и В. Г. Короткина.

В процессе взаимодействия зубца с породой возникает зона предразрушения. В одних случаях эта зона ограничена кони­ческой трещиной, в других — она будет представлять собой ядро с нарушенной структурой материала. Но в обоих случаях порода в окрестности контактной площадки может быть рас­смотрена как полупространство с выемкой, на внутренние стен­ки которой действует некоторое распределенное давление.. Существуют методики, позволяющие рассчитать распределение напряжений в нетронутой части полупространства и на контуре’ выемки для различных эпюр давления. Таким образом, для определения величины силы, при которой произойдет вылом консоли и завершится заключительная стадия процесса раз­рушения, необходимо уметь рассчитать закон распределения давления на внутренние стенки выемки, распределение напря­жений в нетронутой части полупространства и на контуре. Методика решения такого рода задач математически довольно* сложна, но возможна.

Труднее рассчитать углубление зубца в породу при разви­тии промежуточной стадии процесса разрушения, т. е. при фор­мировании ядра предразрушения. В этом случае рассматри­вается материал с непрерывно изменяющимися и неизвестными свойствами. Современная механика твердого тела только раз­рабатывает методы решения подобных задач, основанные глав­ным образом на описании и формализации накопления дефек-, тов и структурных изменений в области разрушения. Имение эта промежуточная стадия является главным препятствием на пути создания расчетно-теоретического метода построения функции P(z).

Что касается математического описания распространения конической трещины, то эта задача пока также не имеет реше­ния, хотя теория равновесных трещин развивается достаточно­успешно. :

Если говорить о процессе внедрения зубца в породу в це-, лом, то необходимо помнить, что он может не ограничиться од­ним скачком разрушения, а состоять из двух, трех, а иногда п более скачков. Расчет этих последующих скачков ослож­няется тем, что его объектом является полупространство с вы­емкой, в котором имеются трещиноватость и нарушение струк­туры, вызванные первым скачком. Наличие градиента давлений г. поверхностном слое породы также может привести к иска­жению картины внедрения зубца, связанному со значительны^ увеличением глубины внедрения, необходимым для вылома консоли. При реальных глубинах внедрения зубцов шарошеч­ного долота выколов может вообще не произойти и, следова­тельно, функция P{z) будет регистрировать главным образом протекание промежуточной стадии процесса разрушения.

Из изложенного ясно, что, хотя отдельные теоретические решения, связанные с функциями P(z), могут и должны быть использованы в исследовательских целях, основным способом получения кривых P(z) должен быть экспериментальный.

Следует указать, что получение зависимостей типа Р (г) экспериментальным путем не является в науке о разрушении новым вопросом. Можно указать большое количество совет­ских и зарубежных исследований, в которых описано получе­ние зависимостей Р (z) или их отдельных элементов в различ­ных условиях и с помощью разных лабораторных установок 18, 19. 20, 22, 24, 31, 36, 38, 41, 43—45, 48, 49].

Для экспериментальных исследований, связанных с взаимо­действием породоразрушающего элемента с образцом ^гррной породы, используются различные лабораторные установки. Наиболее простые из них представляют собой различные коп­ры, в которых необходимая для разрушения энергия накапли­вается движущейся массой. Масса эта может ускоряться за счет свободного падения или с помощью дополнительных меха­низмов. Подобные установки достаточно просты, удобны в об­ращении, их можно использовать в тех случаях, когда необ­ходимо фиксировать заданную энергию удара. Однако полу­чение фиксированной глубины внедрения на таких установках затруднительно. Кроме того, они не позволяют задать опреде­ленный закон внедрения индентора в породу, соответствую­щий кинематике реального породоразрушающего инструмента, а также исследовать влияние скорости взаимодействия зубца с породой, не изменяя энергии удара или других условий экс­перимента.

Для целей, определенных нами выше, удобнее использовать установку, относящуюся к другому типу, именно к такому, в котором внедрение индентора в породу осуществляется при­нудительно, от источника энергии, не связанного с самой уста­новкой. Подобные устройства позволяют в той или иной мере учитывать и моделировать особенности кинематики взаимо­действия зубцов шарошечного долота с забоем.

Американскими исследователями был предложен принцип внедрения индентора в породу с помощью профилированного кулачка (43]. С использованием этого принципа была сконст­руирована специальная установка «КУМ 15», предназначенная для детального изучения единичных актов разрушения и полу­чения их количественных характеристик в условиях, прибли­
женных к условиям породы и реального породоразрушающего инструмента.

Конструкция установки предусматривает возможность про­ведения испытаний с зубцами различных конфигураций на — реальных кернах горных пород. Процесс разрушения происхо­дит в камере, в которой могут независимо воспроизводиться давление столба промывочной жидкости, боковое горное дав­ление и поровое давление внутри образца горной породы. Функция внедрения экспериментального зубца задается профи­лем кулачка. Скорость взаимодействия также может изменяться как за счет профилирования кулачка, так и за счет скорости вращения привода. Устройство установки предусматривает так­же возможность выполнения последовательных ударов зубца по породе с заданным шагом. Измерительная система уста­новки разработана с таким расчетом, чтобы иметь возможность регистрировать величину силы взаимодействия зубца с поро­дой и величину углубления зубца в виде непосредственной записи зависимости P(z).

Техническое описание установки «КУМ 15» и ее характери­стик приведены ниже.

О 1 Z г, мм

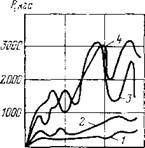
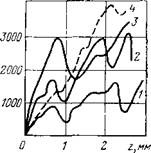
На рис. 7 приведены некоторые экспериментальные зависи­мости P(z), полученные на установке «КУМ 15» при испыта­ниях кернов различных горных пород в атмосферных условиях. Характерной особенностью всех этих кривых является их скач­кообразный характер. С этой точки зрения можно сказать, что характер зависимостей P(z) для различных пород однотипен, хотя по количеству скачков, высоте отдельных пиков, по на­клону упругих участков они могут существенно различаться

Р, кгс

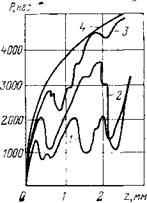
Рис. 7. Экспериментальная зависи — Рис. 8. Экспериментальная зависи­мость силы сопротивления породы от мость силы сопротивления породы от

глубины внедрения зубца (зубец глубины внедрения зубца (условия1

5X1 мм, условия атмосферные: атмосферные, порода—мрамор)

/ — глина; 2— песчаник; 3 — известняк Зубцы: / — 5X0,5 мм; 2 — 5×1,0 мм; 3 —

слабый; 4— мрамор ЮХ! мм; 4—полусферический ч = о мм

между собой. Подобный характер зависимостей P(z) вполне соответствует теоретическим представлениям, изложенным выше. Каждый скачок разрушения соответствует очередному циклу разрушения породы при внедрении зубца и в свою оче­редь обусловливается тремя последовательными процессами, происходящими в горной породе: упругим сжатием, образова-. нием зоны или ядра предразрушения и выколом консоли.

Очевидно, что наклон упругого участка для зубца данной конфигурации будет тем больше, чем выше модуль упругости породы. Величина силы Ри характеризующей первый скачок разрушения, определяется главным образом твердостью породы и в некоторой степени зависит от скорости взаимодействия. Интенсивность падения силы зависит от хрупкости породы. То же самое можно сказать о каждом скачке разрушения.

Когда сила, внедряющая зубец в породу, прекращает свое действие, сопротивление породы падает до нуля с градиентом, определяемым свойствами предразрушенной породы под зуб­цом. Из экспериментальных зависимостей P(z) видно, что эти участки, как правило, имеют больший угол наклона, чем для нетронутой упругой породы, и не всегда линейны. Однако для практических целей вполне возможно аппроксимировать их от­резками прямой.

При получении подобных зависимостей в атмосферных ус­ловиях инденторами различного типа общий характер кривых сохраняется неизменным. Это утверждение справедливо практи­чески для всех типов зубцов, используемых в комплектах во­оружения современных долот: призматических с разными раз­мерами площадки притупления и соотношениями ее сторон, зубцов со сферической вершиной различного радиуса, а также промежуточных модификаций, встречающихся в конструкциях вставных твердоспавных зубцов для мягких и средних пород. На рис. 8 приведены кривые P(z) для зубцов различной кон­фигурации. Исследования механизма разрушения показывают, что глубина зоны предразрушения пропорциональна характер­ному размеру площадки контакта. Очевидно также, что с уве­личением площади контактной площадки сила, необходимая для разрушения, возрастает. Поэтому при увеличении размеров зубца кривая Р(г) вытягивается в направлении обеих осей и, следовательно, при заданной глубине внедрения количество скачков разрушения уменьшается.

Характер кривых P(z) может существенно отличаться при изменении условий внедрения. Наличие перепада давлений в поверхностном слое породы, как правило, значительно уве­личивает силы, потребные для осуществления последователь­ных скачков разрушения. При рассмотрении механизма взаимо­действия индентора с породой было указано, что влияние перепада давлений сказывается не только на величине усилий, но и на характере процесса разрушения. Требуется большее

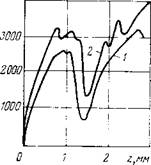
углубление индентора и вылом кон­соли лишается своего хрупкого ха­рактера. Перепад давлений делает породу как бы более пластичной. В результате кривые P(z) приобре­тают более плавный характер и в отдельных случаях могут быть вов­се лишены сколько-нибудь замет­ной скачкообразности. На рис. 9 приведены зависимости P(z) при различных давлениях.

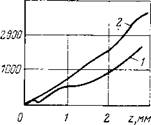
Существенное влияние на харак­тер кривых P(z) при заданном пере­паде давлений может оказывать среда, контактирующая с поверхно­стью породы. Это влияние сказыва­ется в первую очередь для прони­цаемых пород и может быть очень заметным. Снижение водоотдачи раствора к увеличение содержания твердой фазы приводят к тем же последствиям, что и сам перепад давлений, т. е. к увеличению види­мой сопротивляемости породы и сглаживанию кривых (рис. 10).

Рис. 9. Эксперименталь­ная зависимость силы сопротивления породы от глубины внедрения зуб­ца (порода — известняк средний, зубец 5Х XI,0 мм):

/ — атмосферные условия; 2 — р=50 кгс/см2; 3 — р =

=250 кгс/см2; 4 — р = 500 кгс/см2

Р, кгс Рис. 11. Экспериментальная зависи­мость силы сопротивления породы от глубины внедрения зубца (зубец 5X1,0 мм, условия атмосферные, по­рода — известняк крепкий) Скорость соударения: / — 0,4 м/с; 2 — 2,0 м/с

Р. к г с Рис. 10. Экспериментальная зависи­мость силы сопротивления породы от глубины внедрения зубца (зубец 5X1,0 мм, порода — песчаник, р= = 250 кгс/см2)

Раствор: 1 — водоотдача 25 см3/30 мин, со­держание твердой фазы 5%; 2 — водоотда­ча 5 см°/30 мин, содержание твердой фа­зы 25%

33

Наконец, немаловажным фактором, влияющим на динами­ческие характеристики горных пород, является скорость внед­рения в них индентора. С увеличением скорости для некоторых пород происходит определенное увеличение силы сопротивле­ния, а также увеличение жесткости породы. Таким образом, кривые P(z) для больших скоростей взаимодействия имеют более высокие пики скачков и большую крутизну упругих уча­стков (рис. 11).

Проводимые до сих пор кривые были получены при внед­рении зубцов в заранее подготовленную плоскую поверхность — породы. В действительности долото работает на забое с весь­ма неровной и на некоторую глубину предразрушенной поверх­ностью. Сравнение динамических характеристик, полученных на’ гладких и на специально подготовленных, имитирующих забой­ную поверхность образцах, показало, что существенной раз­ницы в характере осциллограмм нет. Заметно только незначи­тельное сглаживание скачков и некоторое снижение усилий..

При экспериментальном получении характеристики P{z) в заданных условиях обычно проводят несколько эксперимен­тов. Это необходимо прежде всего из-за естественной диспер­сии свойств горных пород. При подобных повторных экспери­ментах кривые P(z) обычно сохраняют свой характер, но от­личаются в некоторых количественных деталях. При использо­вании группы таких зависимостей возможны два варианта.

Один из них заключается в том, что в модель процесса1 бурения каждая кривая вводится в натуральном виде и осред­нение выполняется на уровне конечных результатов. При дру­гом варианте может быть найдена одна осредненная кривая; P(z), которая считается представительной для породы данного типа. При осреднении нужно учитывать особенности структуры кривых P(z). Для этого кривые детально анализируются, выде­ляются их характерные элементы и осреднение производится поэлементно. Так, например, положение вершины первого пика (динамическая твердость), характеризующей первый скачок разрушения, осредняется отдельно по глубине и по уровню силы.

В главе 1 уже указывалось, что при расчете скорости про­ходки в ряде случаев должна быть использована зависимость объема разрушенной и отделившейся от массива породы от ’лубины внедрения зубца V(z). Экспериментальное получение кривых V(z) затруднено значительной дисперсией величин измеряемых объемов лунок. Поскольку количество имеющегося в наличии кернового материала обычно невелико, то получение надежных данных для детального построения кривой V(г) мо­жет оказаться весьма затруднительным. Поэтому целесообраз­но установить общий тип зависимостей V {z) на образцах карьерных материалов, обладающих достаточной однород­ностью, как, например, мрамор «коелга», очень часто исполь­

зуемый при лабораторных исследованиях процессов разру­шения.

Поскольку для большинства горных пород вид кривой V (z) оказывается аналогичным, то при работе с керновым материа­лом обычно достаточно получить сравнительно небольшое количество точек.

На рис. 12 приведены несколько кривых V(z) для различ­ных пород. Все они сходны между собой и могут быть аппрок­симированы самыми про — з

отыми аналитическими соот­ношениями типа параболы,

■проходящей через начало координат. Степень этой па­раболической зависимости дд колеблется от 2 до 3.

Экспериментальные ис­следования показывают, что чем слабее порода, тем больший ее объем отделя­ется в атмосферных услови­ях от массива при одной и той же глубине внедрения.

Это правило сохраняется для большинства испытан­ных горных пород.

При детальном построе­нии зависимости V(г) нетрудно заметить, что она имеет волни­стый характер, который исчезает при построении кривых по малому числу экспериментальных точек. Эта естественная болнистость соответствует скачкообразности самого процесса разрушения. Так, например, очевидно, что при углублении, со­ответствующему упругому вдавливанию зубца и вдавливанию во Бремя фазы предразрушения породы, никакой объем практиче­ски от массива не отделяется, но происходят вылом консоли и соответствующее резкое внедрение зубца почти на полную глу­бину предразрушенного ядра. При аппроксимации кривых V(z) для дальнейшего использования эти явления учитывать нецеле­сообразно по следующей причине.

Разрушение породы зубцом реализуется только в том слу­чае, когда разрушаемая поверхность является ненарушенной плоскостью. В действительности же забой всегда представляет собой неровную предразрушенную поверхность. Как показали специальные эксперименты, при разрушении такой поверхно­сти кривые V (z) значительно сглаживаются. Даже при самых малых величинах внедрения зубца в неровную поверхность по­роды происходит хотя и незначительное, но все же заметное отделение ее частиц от массива. Это подтверждается испыта­нием долот на стенде с весьма малой осевой нагрузкой, при

2* 35

которой все же можно зафиксировать некоторую скорость про­ходки. Бурение идет в так называемом «режиме истирания». Таким образом, аппроксимация волнистой кривой V(г) простой степенной функцией не только не вносит существенной погреш­ности в вычисление скорости проходки, но, наоборот, делает эти работы более точными.

Экспериментальные исследования показывают, что в боль­шинстве случаев конфигурация индентора оказывает сравни­тельно небольшое влияние на зависимость V(z). То же можно сказать и о типе разрушаемой горной породы. Это объясняется тем, что наибольшая часть объема образуется крупными куска­ми выламываемой консоли, а траектории вылома отличаются для разных пород только различием в коэффициентах Пуассона v, причем эта зависимость довольно слабая. Таким образом, конфигурации лунок в разных породах близки между собой. Весьма существенное влияние на зависимость V (z) может ока­зать перепад давлений в поверхностном слое породы. При на­личии этого перепада лунки делаются более узкими и, как пра­вило, кривая V(z) проходит ниже, чем при атмосферных усло­виях. При значительных перепадах для некоторых пород воз­можны случаи, когда порода вообще не отделяется от мас­сива, а в ее поверхности остается отпечаток зубца. В этих слу­чаях теоретически скорость проходки равна нулю, а практиче­ски она очень незначительна и возникает за счет отделения не­больших объемов породы при повторных взаимодействиях зуб­цов на неровности забоя.

Выше был приведен краткий обзор экспериментальных ис­следований, связанных с получением зависимостей P(z) и V{z), необходимых для функционирования модели процесса бурения. Количественные результаты подобных исследований, выполнен­ных для разных условий разрушения, их анализ и методика эк­спериментального проведения этих работ, имеющая целью све­сти их практически к минимальному объему стандартных ис­пытаний, будут приведены в следующей главе.

Таким образом, материалы, приведенные выше, позволяют заключить, что при моделировании работы долота углубление каждого конкретного зубца в породу на основании лаборатор­ных испытаний можно сопоставить с соответствующей силой ре­акции породы Р на это углубление. При непрерывном внедре­нии зубца в породу сила Р изменяется в соответствии с харак­тером зависимости P(z). Однако следует иметь в виду, что характеристику P(z) можно использовать лишь для процесса внедрения. При выходе зубца из контакта точка, определяющая состояние системы на графике P(z), не пойдет обратно по той же кривой, так как сила Р, как было указано выше, при об­ратном движении будет уменьшаться до нуля с градиентом, за­висящим от остаточной деформации породы. В этом случае сле­дует пользоваться соотношением

P = P(z’) + k(z — z’)t (2.15)

где z’ — углубление зубца, после которого начинается его возвратное движение; k — угловой коэффициент упругого взаи­модействия зубца с предразрушенной горной породой.

Коэффициент k определяется экспериментально и, как было установлено, не имеет существенного влияния на результаты расчета с использованием зависимости P(z), поэтому его можно определять путем линейной аппроксимации заключительного падающего участка экспериментальной кривой.

Что касается экспериментальных характеристик V{z), то они устанавливают соответствие между глубиной максимального внедрения зубца за цикл его взаимодействия с породой и глу­биной образовавшейся лунки. Эта характеристика используется в дальнейшем для расчета объема породы, отделившейся от массива за определенное время, путем суммирования отдельных объемов V лунок.

Комментарии запрещены.