Бурение грунтовых зондов, установка энергетических колодцев

В России глубинные температуры впервые были исследованы в 1828 г. в шахтах на Урале. Однако широко поставленные геотерми­ческие исследования были проведены на Апшеронском полуострове Д. В. Голубятниковым, который в период с 1906 по 1914 г. иссле­довал свыше 300 нефтяных скважин на Биби-Эйбате и 30 скважин в Сурахапах.

В дальнейшем многочисленные термические исследования сква­жин в различных районах Советского Союза, имеющие большое научное и практическое значение, были проведены М. В. Абрамо­вичем, В. Н. Дахновым, Д. И. Дьяконовым, С. А. Красковским,

Н. Т. Лнндтропом, Ш. Ф. Мехтиевым, Г. М. Сухаревым и др.

Обобщепие и анализ большого фактического материала по заме­рам температур в скважинах дали возможность выявить средние значения геотермических ступеней и градиентов для различных рай­онов мира. В табл. 15 приведены средние величины геотермического градиента и тепловых потоков для различных районов мира [18] по данным Ф. Берча, в табл. 16 — некоторые геотермические сведения, относящиеся к территории СССР.

Таблица 15

Страны и части света	Наибольшая глубина исследова­ния, м	Геотермический градиент, °С/км	Средний тепло­вой поток, мккал / см* * сек
от	ПО	средний
Африка…. …..	3048	7,0	22,3	12,0	1,1
Канада…………………………….	2134	9,1	15,8	13,1	0,96
США…………………………………	2743	18,6	39,0	25,8	1,47
И ран……………………………….	914	—	—	—	0,87
Англия……………………………..	1200	13,3	79,0	34,4	1,33
Тихий океан………………………	1520	40,0	214,0	83,0	1,45
Атлантический океан. .	1440	23,7	54,8	38,6	0,98
Среднее….	—	7,0	214	43,0	1,24

По данным этих таблиц величина геотермического градиента изменяется довольно значительно не только в различных районах, но и в пределах одного и того же района.

Часто в литературе приводится средняя величина геотермического градиента, построенная без учета геологического строения земной коры и равная 32° С 1км (для геотермической ступени это соответ­ствует 30—33 мГС).

Градиент, равный 32°С/к. и, получен в результате измерения тем­пературы во многих скважинах, и современные результаты точпых геотермических измерений подтверждают эту величину.

Так, в табл. 17, составленной по данным Ш. Ф. Мехтпева и

С. А. Алиева [601, приводятся сведения о средних значениях гео­термической ступени по различным пефтяным месторождениям Азер­байджана (глубины от 500 до 2500 м).

Как видно из приведенных в табл. 17 данных, общепринятая ве­личина геотермической ступени, равная 33 мГС, вполне реальна. Однако расчет пластовых температур на больших глубинах с исполь­зованием этой величины, как правило, приводит к значительным ошибкам. Так, если для Карадага принять t0 = 14,5° С и G =

Район исследования	Глубина	Средняя температура на глубине	Геотермическая ступень, м/°С
исследоеа* ння, м	и в интерва­ле исследо­вания, °С	от	до	средняя
Кольский полуостров.	415—450	5,4—4,5	136	170	153
Сибирь………………………..	56,5-118	4,5-5,5	—	_	36,8
Москва………………………..	219-700	9,2-21,5	45,4	59	52.2
Ленинград……………………	170-200	10,2-12,1	37,5	38,5	38,0
Крым…………………………. Краснодарский край	795	40,5	—	—	30,0
(Хадыжп)………………….	—	—	—	—	32,0
Ставропольский край. Грозненский район п Се-	140-452	41-52,3	4,9	22,2	13,5
веро-Осетняская АССР	2010	—	7,5	50,8	29,1
Дагестанская АССР. .	1650	—.	13,9	27,2	21,7
	1000	55,6	_	_	21,4
Чечено-Ингушская АССР	1000	90,7	—	_	12,0
Майкопский район. .	1000	50,4	—	—	25,1
Апшеровский полуостров	1000	47,2	—	—	27,4
Западное Предкавказье	1000	41,9	—	—	31,6
Гурьевская область. .	1000	41,4	—	—	33,3
Нижнее Поволжье. .	1000	28,6	—	—	49,3
Самарская Лука. . .	1000	24,8	—	—	64,3
Башкирская АССР. .	1000	18,4	—	—	82,6
Белорусская ССР. .	1000	23,4	—	—	86,5
Западная часть Украины	50-1650		38,5	50,2	44,3
1000	31,4	—	—	42,9
Донбасс……………………….	450-918	23-27,3	26,3	34,7	30,5
	1000	39,6	—	—	32,0
Кривой Рог………………….	1000	19,5	—	—	112,5
Урал. . ………. ………………	65-1660	4,0-29,7	27	146	86,0
Камское Приуралье.	1000	17,4		—	88,2

= 33 мГС (в литературе принимается еще меньшая величина), то температура на глубине 4120 м по формуле (IV.7) будет равна 140° С, в то время как фактическая температура на этой глубине (забой про­стаивающей скв. 215 (78]) равна всего 98“ С.

Это связапо с тем, что геотермическая ступень, как правило, увеличивается с глубиной [60, 781 и рекомендовавшиеся ранее зна­чения геотермической ступени для месторождений Азербайджана (табл. 17) представляют собой частные значения геотермической ступени на участке непостоянства се [78] и относятся к известной, определенной для каждого района глубине.

Так, еще в 1940 г. М. А. Завацкий, опираясь на даяние замеров температуры в долго простаивающих скважинах, указывал, что средняя геотермическая ступень для условий Апшерона должна быть принята равной 40 л/сС.

Интересные данные были получены А. Б. Цатурянцем и Т. Г. Гаджиевой [771, которые, измеряя температуру в простаива­ющих скважинах месторождения Карадаг, нашли, что для больших

Площадь	Месторождение	Среднее вначение геотермической ступени, л/“С
Агаперонская	Бинагады………………………………………………	33
	Балахапы — Сабунчи — Рамавы. . .	32
	Сураханы…………………………………………….	32,9
	Кала…………………………………………………….	32
	Карачухур-Зых………………………………… …	26
	Локбатан………………………………………………	27
	Биби-Эйбат…………………………………………..	27
	Нефтяные Камни…………………………………..	21
	о. Жилой……………………………………. …	23
Прикаспийско-	Чандагар-Зорат, Сиазавь-Нардарав и
Кубанская	Саадан………………………………………………	32
Прикуринская	Нефтечала…………………………………………….	29
	Кюровдаг………………………………………………	30
Киронабадская	Казанбулаг…………………………………………..	18
	Борсунлы………………………………………………	18
	Нафталан………………………………………………	18
	Дальмамедлы……………………………………….	18

глубин геотермическая ступень равна в среднем 56,08, а не 33 м/°С, как это обычно принимается. При этом на графике tz = / (Z) от­резок, отсекаемый на оси ординат и определяющий некоторую ус­ловную температуру поверхности Земли (0, оказался равным 23,5° С, а не 14,5° С, как это обычно принимается. В соответствии с этим для определения температуры в зависимости от глубины, начиная с 800 м, получаем следующее выражение:

‘2=Ч+4“23’5+аШг

Примерно такое же значение величины <0 приводит в своей работе Е. А. Любимова, рассматривая результаты измерений в скважинах глубиной 2165 м в районе Старой Мацесты.

При этом выражение для определения tz выглядит следующим образом:

П

с глубиной и в интервале 0—1000 м равна 41,7 m/sС, а в интервале 4000-4500 м — 125 мГС.

В результате многочисленных замеров по 286 скважинам анти­клинальной зоны Сураханы — Карачухур — Зых — Песчаный (Ап — шеронскин полуостров) С. Т. Овнатапов и Г. П. Тамразян [63] установили, что с глубипой геотермическая ступень значительно увеличивается. Наименьшие геотермические ступени приурочены к самой верхпей части разреза (глубины менее 200 м) и составляют 15—20 м!°С; на глубинах свыше 1000 м величины геотермической ступени весьма значительны и равны в среднем 40—80 .и/°С, а иногда достигают даже и 100 м/°С.

Хотя авторы [63] не приводят значений f0 , тем пе менее из приводимых ими графиков зависимости tz = f (Z) видно, что при построении зависимости типа (IV.13) величина <0 должна быть принята равной 20—28° С.

В результате термических исследований месторождений При- куринской низменности установлено [17], что по отдельным место­рождениям геотермическая ступень изменяется от 47,3 до 55,5 мГС. По месторождению Кюровдаг в интервале 1370—2728 м геотермиче­ская ступень увеличивается с глубиной от 43,8 до 50,8 мГС.

Увеличение геотермической ступени с возрастанием глубины скважин, пробуренных в районах Северного Предкавказья, на­блюдал и В. А. Покровский.

Начиная с 1958 г., проводились систематические геотермические наблюдения в Азербайджане [И, 17, 60, 70, 77, 78].

Полученные в результате этих исследований величины геотер­мических ступеней приведены в табл. 18.

Таблица 18 Площадь Предельная глубина замера, .и Среднее значение геотермической ступени, м/°С Бинагады………………………………. 1450 50,5 Сураханы……………………………… 2800 77,9 Локбатаи………………………………. 1400 54.9 Биби-Эйбат…………………………… 2300 57,4 Карадаг………………………………… 4100 56,08 Зыря…………………………………….. 1000 41,7 4500 125 Кюровдаг………………………………. 2500 56,5 Еалаханы — Раманы…. 2500 71,4 Нефтяные Камни…………………… 300 20,12 1500 49,37 Саадан…………………………………. 1186 37,2 Сиаэань-Нардаран…………………. 1200 37,5 О. Артема…………………………….. 1900 70,2 Южная складка о. Артема. . 600 80,0 Кюровдаг………………………………. 2728 47,3 Мвшовдаг…………………………….. 1450 55,5 Карабаглы…………………………….. 2870 50,3

Данные этой таблицы свидетельствуют о том, что геотермические ступени более чем в 1,5—3 раза превышают величину принятой сту­пени 33 л/°С.

Естественно, что для расчета пластовых температур требуется точная величина геотермической ступени для конкретной площади. Таких данных для Азербайджана пока недостаточно. Тем не менее

для расчета температур на глубинах, превышающих 1000 л, реко­

мендуется применять формулу (IV. 13), используя среднее значение геотермической ступени, равное 56 мГС (77].

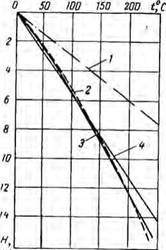
Рас. 23. Изменение темпера­туры горных пород с глу­биной.

Результаты расчетов температур, проведенных по формулам (IV.8), (IV.9)

и (IV. 13), до глубины 15 000 л пока­заны па рис. 23 (лппии 2—4) [60].

На том же рисунке линией 1 показано распределение температур с глубиной согласно зависимости (IV.7).

Как можно видеть из рисунка, фор­мула (IV.13) хорошо сох’ласуется с тео­ретическими кривыми до глубины примерно 7000 м.

Таким образом, в связи с отсут­ствием в настоящее время температур­ных замеров на глубинах свыше 4500 м в первом приближении температуры пород до 7000 л для площадей Азер­байджана можно рассчитывать по фор­муле (IV.13). Однако геотермическая ступень даже для отдельного месторо­ждения непостоянна по своей характе­ристике и в каждом случае должна уточняться.

1 — при Г = 33 м/°С; i — по дан­ным Ы. Д. Дергунова; 3 — по дан­ным К. А. Любимовой; 4 — при Г = 50,08 м/°С. ждепий температура на

Наиболее высокие температуры в настоящео время наблюдаются в сква­жинах Северного Кавказа. Так, в Озек — суатской группе нефтяных месторо- глубине 2500—3000 .и была равна 140—170° С; в Чечено-Ингушетии в скв. 1 Галюгаевская на глубине 5320 л отмечена температура 190° С.

В наиболее глубоких скважинах США: скв. 1 Юниверсити на глубине 7724 м температура равна 181е С, в скв. 1 Румберже на глубине 7316 л 182° С и скв. 1 Монгомери на глубине 7136 л 244° С [751. (

По данным бурения скважин до глубины почти 8000 л можно предположить, что наиболее вероятное изменепие температур на глубине 15 км будет составлять 250—450° С [751.

Of.

В процессе бурения по стволу скважины длительное время цир­кулирует глинистый раствор, который влияет на тепловое поле пород вокруг скважины вследствие разности температур между породами, встреченными скважиной, и промывочной жидкостью. Диаметр зоны нарушения термического режима зависит от диаметра скважины и зоны проникновения промывочного раствора в прони­цаемые пласты, интенсивности и длительности промывки скважины, температуры и физических свойств пород, промывочного раствора и т. д. [84].

Теоретически при циркуляции глинистого раствора температура пород должна измениться на бесконечно большом расстоянии. Од­нако практически в пласте всегда можно выделить границу, за пре­делами которой пласт сохраняет свою естественную температуру.

Расстояние от скважины до точек, где сохраняется естественная температура пласта, называют условным радиусом теплового влия­ния скважины (г0).

В работе 182] при использовании метода последовательной смены стационарных состояний решается задача о распределении темпера­тур в пределах возмущенной области:

*■, Ь + *, In -^г

t= (IV. 15)

1п-^-

гс

Г„ «£ Г sg Г0,

где tB — начальная температура пористой среды; fp — температура промывочной жидкости у забоя; гс — радиус скважины; г — рас­стояние от оси скважины до точки с температурой t; г0 — радиус теплового влияния скважины, в пределах которого распределение температуры считается стационарным.

Используя зависимость (IV.15), можпо построить кривую распре­деления температуры в пласте t = / (г).

Вполне очевидно, что при г = гв t = f_, а при г = r0 t — tu.

Однако вычислить по зависимости (IV. 15) радиус теплового влия­ния нельзя, так как для этого необходимо знать закоп распределения температур в пласте t — / (г) для каждого конкретного случая.

Анализ температурных исследований, проведенный по обвод­нявшимся эксплуатационным скважинам, дает основание Г. В. Ко — стрюкову и А. Д. Голикову полагать, что, несмотря на высокий темп закачки и значительное обводнение нагнетаемой водой пласта, зона влияния холодной воды на его температуру не превышает 400—500 м. Следовательно, радиус теплового влияния нагнетатель­ных скважин не превышает приведенных величин (для Ромашкин — ского месторождения).

Из данных зарубежной литературы следует, что радиус тепло­вого влияния г0 увеличивается в зависимости от времени промывки

(tj), причем г0 = r0 (tj) зависит от вида граничных условий. В част­ности, нри г0 г0 приближенный радиус теплового влияния можно определять по соотношению

(IV.16)

г0*=&2уг яаТ[,

где а — коэффициент температуропроводности; хг — время про­мывки.

Справедливость уравпения (IV.16) для вычисления г0 в буря­щейся скважине может быть проверена лишь экспериментально.

Моделируя электропрогрев пласта мощностью h = 2 м, пройден­ного скважиной радиусом г0 = 0,1 м, авторы работы [88] приводят критериальные зависимости для расчета распределения температур в пласте при различных мощностях электроподогревателя. Анализ этих зависимостей показал, что радиус теплового влияния электро­подогревателя при прочих равных условиях тем больше, чем выше мощность нагревателя. С увеличением расстояния влияние мощ­ности электронагревателя существенно ослабевает. Описанное явле­ние, очевидно, будет наблюдаться и в бурящейся скважине, если подогревателем считать некоторый столб промывочной жидкости, обладающей определенной тепловой мощностью, или долото, выде­ляющее тепло при разрушении пород.

С этой точки зрения методика моделирования, разработапная для электроподогревателей в работе [88], может во многом облегчить работу по моделированию распределения температур в породах, пройденных бурящейся скважиной.

Т. К. Меликов рассмотрел зависимость радиуса теплового влия­ния скважины от продолжительности прокачки. Считая изменение температур вокруг скважины концентричным и допуская, что пара­метры пород п жидкости, заполняющей скважину, одинаковы, он вывел следующую формулу:

(IV.17)

где Я — теплопроводность пород в контурной зоне; h — мощность пласта; Q — тепло, приходящееся па единицу длины скважины; ta — температура пласта; tr — температура жидкости в скважине; г, — продолжительность прокачки жидкости в скважине.

На оспове формулы (IV. 17) и данных термических измерений в разрезе калинской свиты Биби-Эйбатского нефтяного месторожде­ния сделан вывод, что при равных значениях продолжительности прокачки г0 для песков и глин различен. Изменение радиуса те­плового влияния от продолжительности прокачки происходит по экс­поненте, п при значениях хг менее 10 ч оно ничтожно.

В работе Г. А. Череменского [84] описана методика расчета радиуса теплового влияния непосредственно для бурящейся сква­жины. Г. А. Череменский использовал уравнепие теплопровод­
ности, полученпое для цилиндрического источника тепла постоянной мощности. Расчетная формула имеет вид (971:

(iv.is)

где q — тепловая мощность, выделяемая (поглощаемая) промывоч­ной жидкостью в единицу времени на единицу длины скважины;

— теплопроводность пород; At — изменение температуры на расстоянии г от оси скважины; тх — время нарушения теплового состояния пород; а — температуропроводность пород; гс — радиус скважины.

В работе [84] на основе формулы (IV.18) приведены кривые за­висимости A t XJq от г и разработана методика определения г0. Для этого по методике Г. А. Череменского необходимо задаться значением удвоенной относительной погрешности замеров темпера­тур, так как в пределах последней замеры температур неточны. Тогда значение текущего радиуса г принимает конкретпое значение, соответствующее радиусу теплового влияния г0. Таким образом, величина радиуса теплового влияния будет изменяться в зависи­мости от степени точности замера температур.

Так, при удвоенной относительной погрешности, равной 0,1, для а — 0,008 мг/ч, = 6 — f — 150 суток радиусы зоны нарушения равны 1—4,5 м. При погрешностях измерения, в четыре раза мень­ших, и при тех же значениях а и xt радиус зоны парушения дости­гает 2—10 м [841.

Если условно замерять температуру в пласте исключительно точным термометром, то можно будет уловить изменение темпера­туры на бесконечном расстоянии от скважины, т. е. в этом случае г о будет равен бесконечности.

Задаваясь величинами удвоенной относительной погрешности измерений 2 Е, температуропроводности породы а и величинами т по кривым A t а/ д = / (г) согласно методике, изложенной в работе

Таблица 19 Удвоенная относительная погрешность 2Е Радиус теплового влияния ч0, м о=0,001, 1=150 о=0,008, 1=6,25 О = 0,008, 1=50 о = 0,008, 1= 150 0 = 0,008, 1 = 500 0,1 1.7 1 2,7 4.5 8,4 0,2 9,8 0,5 1.4 2,2 4 0,3 0,4 0,25 0,65 1.2 2 0.4 0,22 0,15 0,35 0,6 1,2 0,5 0,13 0,75 0.2 0,3 0,6 г; Примечание. i=i,-f-i_; -^ = ^ = 0,147 суток.

[84], найдем значения г„ для различных конкретных случаев {табл. 19).

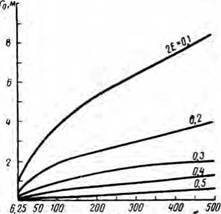
На рис. 24 показано изменение величины радиуса теплового влия­ния скважины в зависимости от времени промывки при различных

ъ. сутки Рис. 24. Зависимость величины радиуса теплового влияния скважины от вре­меня промывки при различных удвоен­ных относительных погрешностях из­мерения температур.

значепипх удвоенной относи­тельной погрешности изме­рений.

Из рис. 24 видно, что интен­сивность роста г о уменьшается с увеличением погрешности из­мерений.

С уменьшением же темпера­туропроводности пород а вели­чина г0, как правило, принимает значения, более низкие, чем для пород повышенной темпе­ратуропроводности. Это хорошо видно из табл. 20, составленной согласно табл. 19 для одних и тех же значений т (т — = 150 суток).

Из табл. 20 также следует, что при одних и тех же значе­ниях т при увеличении погреш­ности измерений величина раз­ности между значениями г„ уменьшается.

Т а б л ч д а 20 2 Е <Г=0,008 о"=0,001 ri— i? й * r# 0.1 4,5 1,7 2,8 0,2 2,2 0,8 1,4 0,3 1.2 0,4 0,8 0,4 0.6 0,22 0,38 0,5 0,3 0,13 0,17

Комментарии запрещены.