Бурение грунтовых зондов, установка энергетических колодцев

Рассмотрим понятие величины скорости проходки. Очевид­но, что мгновенная скорость любой точки корпуса долота, рассматриваемого как недеформируемое твердое тело, не мо­жет характеризовать величину скорости проходки, так как она определяется не только продвижением забоя и его изменяю­щейся конфигурацией, но и сложным движением нижнего сече­ния колонны бурильных труб. В то же время понятия мгно­венной скорости продвижения забоя также не существует, ибо последовательные во времени забойные поверхности не явля­ются конгруэнтными. Таким образом, следует рассматривать скорость проходки как величину интегральную во времени и ь пространстве.

Область оптимальных режимов бурения для определенной конструкции долота выбирается на основе интегральных пока­зателей бурового процесса, таких, как проходка за рейс, рей­совая скорость или стоимость 1 м проходки. В основе расчета этих интегральных показателей лежит величина скорости про­ходки, наряду с нормативными данными и экспериментальными зависимостями, касающимися стойкости элементов конструк­ции долот. Вопросы определения непосредственно интегральных показателей бурения и их оптимизации рассмотрены в главе б.

С позиции математического моделирования процесса взаи­модействия инструмента с породой, принятой в данной книге, необходимо исследовать закономерности разрушения горных пород, определяющие интенсивность углубления забоя сква­жины.

Если мысленно выделить некоторую точку забоя и следить ьо времени за ее продвижением в направлении оси скважины, то получим ступенчатый график, в котором периоды неподвиж­ности сменяются быстрым продвижением. Количественная оцен­ка этих временных интервалов показывает, что в зависимости от выбранной точки на забое, скорости вращения и конструк­ции вооружения долота время между двумя периодами актив­ного продвижения колеблется по грубой оценке от 0,02 до 3 с а время собственно разрушения—от 1,5 до 20 мс. Таким об­разом, время покоя превышает время продвижения более чем на порядок, а точнее в 13—15 раз. Общее продвижение по:

Еерхности забоя представляет собой совокупность неодновре­менных и не вполне одинаковых импульсных продвижений отдельных ее точек. Будем считать, что скорость проходки мо­жет быть определена, как средняя скорость за время t любой произвольно выбранной точки забоя. В общем виде можно записать

, N(t)

(1Л)

;=i

где и —скорость проходки, обычно называемая механической скоростью проходки или бурения, чаще всего обозначается о мех (имеется в виду прежде всего скорость бурения неизно­шенным долотом); t — текущее время; i — индекс каждого акта взаимодействия венца долота с породой в окрестности выбран­ной точки забоя; 2*— углубление выбранной точки забоя при очередном взаимодействии зубцов данного венца с породой в окрестности этой точки; N(t) —общее число ударов зубцов в окрестности выбранной точки, учитываемых при расчете ско­рости проходки.

в

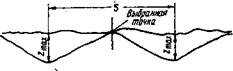
Рис. 1. Схемы продвижения выбранной точки забоя

Здесь имеется в виду, что очередное взаимодействие зубцов с породой в окрестности выбранной точки на величину 2тах вызывает углубление самой точки на величину г,-, которая в общем случае не равна 2тах- При прохождении венца ша­рошки через выбранную точку шри каждом обороте долота может произойти одно (рис. 1, а) или два углубления

(рис. 1,6) выбранной точки или вовсе не произойти углубления (рис. ,в) в зависимости от расстояния предыдущей и после­дующей точек контакта зубцов с забоем от выбранной точки и от величины углубления зубцов zmax. Возможно, конечно, что очередной удар придется в точности на выбранную точку. В этом случае Zi = zmax.

Когда углубление выбранной точки осуществляется двумя последовательными зубцами одного венца (рис. 1,6), фактиче­ское углубление равно наибольшей из этих двух величин. При этом, однако, нужно учитывать взаимное влияние лунок. Если лунки частично смыкаются, то углубление выбранной точки определяется конфигурацией поверхности соединения лунок. Ниже будут приведены некоторые результаты эксперименталь­ных исследований этого вопроса. В случае, когда расстояние между соседними ударами меньше оптимального (для данного углубления zmax), то углубление выбранной точки Zi = zmax. Оптимальным расстоянием мы называем такое, при котором происходит полный скол целика породы между двумя сосед­ними лунками, так что снятие слоя на глубину zmax происходит за один оборот долота.

Реализация одного из указанных вариантов при каждом прохождении шарошки зависит, кроме углубления zmax, еще от шага зубцов

S = 2r sin —, (1.2)

К

где К — количество зубцов на венце; г—средний радиус рас­сматриваемого венца.

Практически нет возможности вычислить точную величину v через предел последовательности Zi. Достаточно рассмотреть ограниченную последовательность углублений zt — с тем, чтобы определить скорость v с заданной погрешностью.

Рассмотрим расчет последовательности значений 2г-, исходя из некоторой упрощенной схемы образования лунок. В част^ ности, пока воздержимся от учета возможного скольжения зуб­цов, т. е. не будем рассматривать горизонтальную компоненту траектории внедрения зубца.

Определим прежде всего расстояние очередного удара зуб­ца от рассматриваемой точки забоя. Если обозначить через R средний радиус кольцевого участка забоя, обрабатываемого данным венцом, то без учета скольжения центральный угол точек двух последующих ударов 26 можно рассчитать по фор­муле

26 = 2 arc sin —. (1.3)

2 R

Тогда дуговое расстояние S" между точкой удара, располо­женной наиболе близко к рассматриваемой точке, опреде­лится как разность между длиной средней окружности 2nR

и длиной дуги, включающей наибольшее возможное целое число отрезков дуг 2R6 (индекс «два штриха» в дальнейшем будет относить к ударам до выбранной точки, а «один штрих» — после нее). При каждом последующем проходе это расстояние будет увеличиваться на некоторую величину RQ, где 0 — цент­ральный угол остаточной дуги, пока не достигнет величины 26, после чего образуется новая величина остаточной дуги и про­цесс будет продолжаться. Образующаяся последовательность в угловых величинах может быть записана выражением

2я — f — 0(

26

2

6

‘i—i

0

(1.4)

где

— целая часть числа

2л + 0,_, — 26

2 6

Очевидно, что дуговое расстояние очередного удара зубца от рассматриваемой точки может быть определено как

(1.5)

Будем считать исходным положением для расчета удар по гладкой поверхности в самой выбранной точке. Тогда при каж­дом проходе венца удар после выбранной точки предшествует удару до нее. Поэтому можно записать

(1.6)

5; = s;_, + 5.

Прежде чем перейти к дальнейшему расчету, необходимо задаться некоторой моделью сечения лунки разрушения. Речь идет о сечении цилиндрической поверхности радиусом R с об­разующими, параллельными оси скважины. Затем эта цилин­дрическая поверхность разворачивается на плоскость. В этом сечении лунка описывается в общем виде некоторым урав­нением

(1.7)

z = f(s)

где z — текущая координата лунки вдоль оси z, направленной параллельно оси вниз и имеющей начало на условной началь­ной поверхности; s — текущая координата лунки вдоль оси s, направленной в нашей схеме вправо и имеющей начало в вы­бранной точке на условной начальной поверхности.

Соответственно для лунок, образуемых t-м проходом венца после выбранной точки и до нее, уравнения должны быть за­писаны со следующими индексами:

(1.8)

Для определения вида функции (1.7) воспользуемся резуль­татами экспериментальных исследований, посвященных изуче­нию конфигурации лунок разрушения. Установлено, что, вне зависимости от объема лунки, ее общие очертания остаются примерно схожими. Лунка представляет собой полость, близ­кую к перевернутому эллиптическому конусу, основание кото­рого расположено на поверхности породы. В действительности лунка имеет более сложную конфигурацию, однако подобная аппроксимация позволяет получить удовлетворительное коли­чественное описание геометрических параметров лунки [7, 34]. Обозначив через |3 половину угла ее раствора, получим

(1.9)

Z Zmax i S Ctg P.

Здесь знаки «—» и «-у» относятся соответственно к правой и левой частям сечения лунки.

Для некоторых горных пород угол р оказывается не зави­сящим от глубины лунки £34]. Так, для мрамора (3 = 70°. В этом случае z = 2max—0,365 s. В других случаях можно пользоваться экспериментальными зависимостями различного вида [7, 34], связывающими угол (5 с глубиной гтах. Формула (1.9) дейст­вительна, когда отсутствует взаимное влияние соседних лунок. В этом последнем случае она должна быть заменена экспери­ментально полученными эмпирическими соотношениями. Нако­нец, если расстояние между соседними ударами меньше или равно оптимальному, то Zi = zmax. В результате специально по­ставленных экспериментов в расчетные данные могут быть внесены определенные коррективы. Однако общая структура алгоритма сохраняется.

1

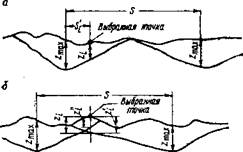
Формула (1.9), описывающая принятую модель сечения лун­ки, приведена для случая, когда начало координат расположено ь точке удара. Для общего случая с учетом расстановки соот­ветствующих индексов можно записать (рис. 2):

Выбранная точна

Z

Рис. 2. Схема к расчету продвижения выбран­ной точки

max ~r

(1.10)

^гпах "Ь С (sc Si),

% i ^max ~h Z i — f — С (s; Si) ,

^max “i~ % i £ I Si |, (111^

z’i = 2max + ‘Zi~csi — Sc |.

Здесь c = ctgP; s/, 2/ и s’., z — — текущие координаты сече­/S /N

ния лунок справа и слева от выбранной точки; 5′., z и S’, z—• координаты точки соприкосновения зубца с поверхностью забоя при г-м проходе справа и слева от выбранной точки.

Дальнейшие расчеты являются построением алгоритма фор­мирования забоя в окрестности ± S от выбранной точки, исходя из предварительного допущения независимости углубления zmax и формы лунки от положения точки удара. Как уже указыва­лось, экспериментальные коорективы этого допущения могут быть учтены. Сложность расчета заключается главным обра-

/ч

зом в определении величин ег-, поскольку без специальной про­верки неясно, с какой из предыдущих лунок возникает контакт

при г-м проходе. Поэтому следует сравнивать величины Z{-j, где /= 1; 2; 3 и т. д.

Однако нет надобности осуществлять такую проверку для всех предыдущих проходов. Действительно, точки контакта зуб­цов с забоем периодически удаляются от выбранной точки и снова возвращаются к ней. Число проходов в этом цикле можно определить по формуле

— = . (1.12)

2л — f — 0О 28

. S, — " ‘ п

# 2л — 0„ — 28

Здесь квадратные скобки означают взятие целой части вы­ражения, заключенного в них.

Достаточно проверить возможность контакта очередного зубца с тем количеством лунок, которое соответствует двум таким циклам, т. е. максимальное значение jmax будет

(1.13)

.. . 5

/шах

S,

Эту проверку следует производить для лунок, центр которых расположен как до выбранной точки, так и после нее.

Теперь можно перейти к вычислению фактического значения

величин г,-.

Вычисление координат точек соприкосновения зубцов с фак­тической поверхностью обнажения требует проверки следующих вариантов (и, соответственно, введения некоторых новых обо­значений) :

— соприкосновение зубца при г-м проходе справа от вы­
бранной точки с поверхностью одной из предыдущих лунок, также образованных ударами справа от выбранной точки,

2 / / zi—j — j~ zmax с | Si S{—j |, (1.14)

— соприкосновение зубца при г-м проходе справа от вы­бранной точки с поверхностью одной из предыдущих лунок, образованных ударами слева от выбранной точки,

*-i j z i—j — f — zmax с | Si Si—j |, (1 • 15)

— соприкосновение зубца при г-м проходе слева от выбран­ной точки с поверхностью одной из предыдущих лунок, также образованных ударами слева от выбранной точки,

7ц = г-_/ + zmax— cjSi — s’i-j; (1.16)

— соприкосновение зубца при г-м проходе слева от выбран­ной точки с поверхностью одной из предыдущих лунок, обра­зованных ударами справа от выбранной точки,

zij zi—j zniax с | Si Si—j |. (1.17)

После этой проверки при j= 1, 2, …, /шах определяется наи­/ч

/S

большее значение из величин Zj/ и z*/, которое и является

фактической координатой г/ точки соприкосновения зубца с за­боем при г’-м проходе справа от выбранной точки. Ее можно использовать для расчета процесса формирования забоя.

Аналогичным образом определяется величина zj, т. е. коорди­ната точки соприкосновения зубца с забоем при г-м проходе слева от выбранной точки.

Дальнейший расчет углубления выбранной точки произво­дится следующим образом. В формулы (1.11) следует подста­вить координаты выбранной точки, т. е. s/=0 или s’{ =0. Тогда получим углубление выбранной точки, как наибольшую величину из

zго ~ ^г -(- ^шах cSi,

ZiO Zi — I- ^шах cS(.

Если z’i0<0 или zt’0<0, то считаем, что z-0 =0 и z"i0 =0. Наибольшая из этих величин Zio сравнивается с полной глу­биной забоя в выбранной точке по предыдущему проходу

<1Л9>

г=о

Таким образом, очередное углубление за проход равно Zi=zl0 — Zt-i. (1.20)

Если 2г<0, то считаем, что z* = 0.

Для дальнейшего расчета остается определить полное углуб­ление-забоя

1i = Zi—i — f z(. (1.21)

В качестве примера приведем таблицу расчетов при следую­щих исходных данных:

Zmas = 2 мм; с = ctg = 0,365; 5=10 мм; 5 = 5,5 мм; 6 = 7°; Л? = 41 мм.

В табл. 1 графы обозначены номерами от 1 до 23, содер­жание которых следующее.

В верхней части таблицы:

1 — i;

2 — не заполняется;

3 — 5,- [формула (1.6)];

4—8 — z’.. для / = 1, …, 5 [формула (1.14)];

9—13 — Zij для / = 1, …, 5 [формула (1.15)];

14—18 — z’._. для / = 1, 2, …, 5 (выбирается как наибольшее значение из строки, соответствующей проходу i—у);

19 — г/ (выбирается как наибольшее положительное значение из граф 4—13);

20 — z0{ [формула (1.18)];

21—Z,_! [формула (1.19)];

22 — Zio (выбирается как наибольшее значение при сравнении соответствующих строк 20-х граф верхней и нижней частей таблицы);

23 — г, [формула (1.20)].

В нижней части таблицы:

1 — г;

2 — 0г- [формула (1.4)];

3 — 5[ [формула (1.5)];

4—8 — z".. для у = 1, …, 5 [формула (1.16)];

Л

9—13 — z. для/=1, …, 5 [формула (1.17)];

14—18 — z. . для у = 1, …, 5 (выбирается как наибольшее зна­чение из строки, соответствующей проходу г—у);

19 — z (выбирается как наибольшее положительное значение

из граф 4—13);

20 — z"i0 (формула 1.18).

В графе 23 верхней части табл. 1 даны последовательные углубления выбранной точки забоя при каждом проходе через нее венца шарошки долота.

4	5	6	7	8	9	1 0	1 1	12
— 1 ,65	—	—	—	—	— 1 ,65	—	—	—
— 0,61	0 ,96	_	—	—	— 1 ,65	0 ,96	—	—
1 ,92	0,43	-0 ,08	—	—	— 0,69	— 2 ,70	— 0,08	— 1,13
2 , 88	0,88	I,48	-1,13	—	— 0,17	— 1 ,73	— 3,74
2 ,27	2 ,35	2 ,43	— 1,13	1 ,48	— 0 ,1 7	2 , 88	0 ,88	— 1,13
3 ,83	3 ,3 1	3,40	2,43	— 0,08	0,78	— 1 ,22	1 ,84	— 0,17
4 , 80	2 ,79	4 ,36	3 ,40	1 ,39	1 ,76	0,70	— 1 ,30	— 0 ,25
— 0,61	—	~	—	—	— 0,61	—	—	—
0,96	0,43	_	_	—	—3,22	0,43	—	—
1 ,92	— 0 ,08	1 ,48	_	—	1 ,39	— 2,17	1 ,48	—
1,3 1	1 ,39	1,48	—1,13	—	— 1 ,30	-1.22	—4 ,79	— 1,13
2 ,43	2 ,35	2 ,43	1,48	— 0 , 08	— 0,34	— 0,25	— 0,17	—3 ,74
3,40	1 ,39	3,40	2 ,43	0,43	3,31	0,70	0,78	0 ,88
4 ,36	2 ,35	0 ,34	3,40	1 , 39	4,27	4 , 6	1 ,76	1 ,81

Продолжение табл.

14	15	16	17	1 8	19	20	2 1	22	23
					0	2 ,00	0	2 ,00	2 ,00
0			_	_	0	0	2 ,00	0	0
n	0		_	_	0,96	1 ,92	2 ,00	1 ,92	0
0 ,96	0	0	_	_	1 ,92	1 , 84	2 ,00	3,40	1 ,40
1 ,92	0 , 96	0	0	_	2 ,88	1 ,76	3,40	1 ,76	0
2 ,88	1 ,92	0 ,96	0	0	2 ,88	4 ,36	3,4 0	4 ,36	0 ,96
2 , 88	2 , 88	1 ,92	0 ,96	0	3 , 83	4,27	4,36	4 ,36	0
3 ,83	2 ,88	2 ,88	1 ,92	0,96	4 ,80	4,20	4 ,36	6 ,36	2,00
					0	2 ,00	_		—
0	_	_	—	—	0	0	—	—	—
0	0	_	_	_	0 ,96	1 ,39	—	—	—
0,96	0	0		—	1 ,92	3,40	—	—	—
1 ,92	0,96	0	li	—	1 ,48	0 ,3 5	—	—	1
1 ,48	1 ,92	0 ,96	0	0	2 ,43	2 ,3 4	—	—
2 ,43	1 ,48	1 ,92	0 ,96	0	3 ,40	4 ,36	—	—
3,40	2 ,43	1,48	1 ,92	0 ,96	4 ,36	6,36

Учитывая формулу (1.1), для ограниченного числа прохо­дов N можно записать

N

у-0,06 -^2*0 (1-22>

i=i

где v — скорость проходки в м/ч; « — скорость вращения до* лота в об/мин.

На основании данных табл. 1 и формулы (1.22) v в дан­ном случае будет равна 0,048 п. Например, при « = 400 об/мин скорость проходки составит 19,1 м/ч.

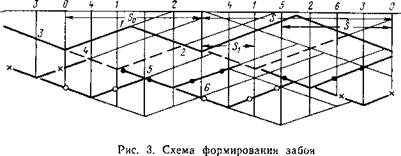
Процесс образования забоя, описываемый изложенным выше алгоритмом, можно представить графически (рис. 3). При этом еидно, что даже при выбранной нами весьма условной схеме образующийся участок забоя представляет собой сложную,, меняющуюся при каждом обороте долота, поверхность.

Выдранная точна

В действительности, как уже указывалось выше, процесс формирования забоя шарошечным долотом происходит намного сложнее. В приведенном алгоритме учитывается взаимодейст­вие только двух соседних зубцов одного венца при простейшем предположении, что их максимальные углубления и конфигу­рация лунок остаются неизменными. Если удастся дополни­тельно установить зависимость величины максимального углуб­ления и формы лунки от места и условий контакта данного зубца с забоем, то структура расчетной схемы в принципе не изменится. Нужно будет только подставлять для каждого про­хода соответствующие значения zmax и функции z,- = f(Si)- Аналогично, если ввести определенную величину проскальзыва­ния шарошки, то нетрудно определить поправки для угла оста­точной дуги 0,. В самом деле, при расчете по формулам (1.3) и (1.6) можно подставить вместо шага S величину

SC = S( l+i^, (1.23)

V Пш J

где 5С — шаг с учетом скольжения; пт — расчетное число обо­ротов шарошки; Апш — изменение числа оборотов шарошки в результате скольжения;

Пф — фактическое число оборотов шарошки; Апш/пш — мера скольжения шарошки.

Совершенно очевидно, что влияние конфигурации забоя на характер образовавшейся лунки может быть установлено толь­ко экспериментально. При проведении экспериментов важно сделать оценку расхождений между идеализированной схемой V действительной, чтобы ввести в случае необходимости соот­ветствующие поправки. При этом для каждого конкретного слу­чая должна определяться осредненная конфигурация лунки.

На основании изложенного можно заключить, что сущест­вует принципиальная возможность рассчитать механическую скорость бурения в заданных условиях, если удастся найти спо­соб определения глубины внедрения каждого контактирующего зубца долота zm&x. Чтобы понять сложность этой задачи, на­помним, что даже в рассмотренном выше одном венце, зубцы могут находиться в контакте с забоем не по одиночке, а одно­временно. В зависимости от сочетания шаг зубцов и величины их углубления в одновременном контакте с забоем могут ока­заться два, три и даже более зубцов. При этом во времени происходит перераспределение нагрузки между ними. К тому же забой разрушается одновременно всеми шарошками долота, юбщее количество венцов которых может доходить до десяти, и более. В каждый момент времени с породой взаимодействует целый ряд зубцов различной конфигурации, находящихся в раз­личной стадии внедрения. Поэтому для определения величины •2тах следует учитывать конструкцию данного конкретного до — .лота, его кинематику и прочностные характеристики разбури­ваемой породы. Кроме того, существенное влияние на величину углубления зубцов zmax оказывают колебания колонны буриль­ных труб, возбуждаемые взаимодействием долота с забоем. Таким образом, для определения величины гтах необходимо со- •ставить систему уравнений, описывающих кинематику шарошек долота и колонны бурильных труб. Система таких уравнений по сути дела являлась бы детерминированной моделью про­цесса бурения. Решение этой системы должно быть построено таким образом, чтобы результатом его было получение вели­чины 2тах — Это возможно только в том случае, если в гранич­ные условия системы будут входить характеристики сопротив­ляемости породы. Последние, по-видимому, могут быть полу­чены только экспериментальным путем. Построению математи­ческой детерминированной модели процесса бурения посвящена глава 2.

Как уже указывалось, целью построения модели процесса бурения является определение 2тах. Выше был показан один из возможных принципиальных вариантов расчета скорости проходки v с использованием величины гтах. Однако он отнюдь не является единственным. В зависимости от поставленной задачи могут быть использованы несколько отличные приемы. Если исследованию подлежит процесс формирования забоя в целом, в частности, возникновение реек, ухабов и других осо­бенностей забойной поверхности, то целесообразно не ограни­чиваться рассмотрением одной выбранной точки на поверхности забоя. Процесс образования и соединения лунок, описываемый выше, можно рассчитать вдоль каждой из кольцевых дорожек, обрабатываемых одним или несколькими венцами. Таким обра­зом, можно получить полную картину продвижения всего забоя в целом.

Для этого следует разделить всю длину кольцевой дорожки, обрабатываемой данным венцом, на определенное количество участков, достаточно мелких по сравнению с размерами лунки разрушения. Координаты поверхности забоя по выбранному кольцу отсчитывают от условной плоскости, перпендикулярной к оси скважины, как это было показано выше. Координаты заносят в таблицу, хранимую в памяти ЭВМ. Они представ­ляют собой табличное описание геометрической конфигурации кольцевого участка забоя после Его оборота долота (Его про­хода).

Суть расчета постепенного изменения этой конфигурации во времени заключается в следующем. При контакте очередного зубца с забоем по указанной таблице определяют координату точки контакта, суммируют ее с полным углублением данного зубца и получают координату вершины лунки. Используя фор­мулу (1.9) или подобную ей, можно вычислить координаты вновь образовавшегося участка поверхности слева и справа от точки контакта и занести их в очередную строку таблицы.

При взаимодействии с забоем следующего зубца обнажается еще один участок забоя и еще несколько значений координат в таблице. Естественно, что обнажение каждого нового участка может отчасти затрагивать и предыдущий, так как лунки в определенных условиях перекрываются. В любой момент можно вывести на печать последние значения координат забоя па каждом участке и таким образом зафиксировать его полную конфигурацию.

В отличие от рассмотренного выше варианта, учитывающего продвижение выбранной точки, в данном случае координаты вновь образующихся лунок следует рассчитывать по формуле

z = гшах* + Zi—. k rb (s — Sik) Р> (1-24)

где индекс k относится к £-му удару Его прохода; Z,-_i. ft — координата забоя в точке k-то удара, образовавшаяся при предыдущем проходе; Sik— координата точки k-ro удара при /-м проходе.

Заметим, что текущая координата s может принимать толь­ко дискретные значения в соответствии с выбранной системой разделения длины кольцевого участка забоя на интервалы

s = mRAQ, (1.25)

где А0 — угловой размер интервала; т — его порядковый но­мер, причем Os£ms£2n/A0.

При расчетах по формуле (1.24) координаты точек кон­такта с забоем очередных зубцов могут не совпадать с гра­ницами интервалов разбивки кольца забоя. Поэтому очередное углубление зубца, относящееся к точке 5^, необходимо за­писать в таблицу в графу, соответствующую ближайшему дис­кретному значению величины mRAQ,

где квадратные скобки означают взятие целой части от дроби, заключенной в них. Однако величину Sik при вычислении профиля образовавшейся лунки следует брать такой, какая получается из расчета движения венца.

Для г-го прохода величины Sih рассчитывают с помощью слегка видоизмененной формулы ( 1.6), а именно

Sik = Si-i + ks, (1.27)

где 5 —координата последнего удара предыдущего про­

хода, определяемая с помощью формул (1.4) и (1.5).

Для определения другой координаты забоя в точке удара — приходится прибегнуть к линейной интерполяции ее значения между интервалами т и m-1-l, т. е. считать, что

Zi-l. k = — (Zi-l. m + Zi—l. m+l)- (1.28)

При расчете по приведенной схеме величины zmax могут изменяться от удара к удару. Их вычисляют каждый раз из решения системы уравнений движения шарошек и колебаний колонны бурильных труб, составляющих математическую мо­дель процесса бурения. —

Заметим, что при вычислении скорости бурения по движе­нию выбранной точки не было необходимости рассчитывать работу всех венцов долота. Однако при исследовании форми­рования забоя, если схема моделируемого долота принята многовенцоЕОЙ, приведенный выше расчет следует проводить параллельно для всех венцов, что позволит в случае надоб­ности воспроизвести пространственную форму забоя в любой момент времени процесса бурения.

Что касается скорости проходки, то она может быть вычис­лена по формуле (1.22), применимой к любой графе таблицы, в которой фиксируются изменяющиеся координаты точек забоя.

В заключение укажем еще на один возможный и довольно простой способ вычисления скорости проходки v через установ­ление экспериментальной зависимости объемов образующихся — лунок V от их глубины zmax.

В общем виде можно записать

1 1 Nlt)

“ = т!1тгт2 21’”*»’ "29)

km п—

где N — общее количество ударов по забою за время t; F — площадь сечения скважины; п, k, т — индексы соответственно зубца, венца и шарошки.

Таким образом, производится суммирование объемов лунок разрушения, производимых зубцами k-то венца пг-й шарошки, и затем вторичное суммирование объемов лунок по всем вен­цам и шарошкам.

При таком подходе должны быть получены эксперимен­тальные зависимости ^„(Zmax) Для зубцов всех типов, пред­ставленных в данной конструкции долота. Как будет показано ниже, подобные зависимости связаны с размерами и конфигу­рацией зубцов достаточно простыми соотношениями, и поэтому практически бывает достаточно получить экспериментальную функцию K(zmax) для эталонного зубца стандартной формы и размеров.

В настоящей главе мы попытались показать, что процесс формирования забоя зубцами шарошечного долота сводится к некоторой принципиальной схеме, которая может быть фор­мализована и что с помощью определенного набора стандарт­ных лабораторных испытаний эта схема даст возможность вычислить скорость проходки в количественном выражении, если для заданных условий бурения известна величина углуб. ления зубцов zmax.

Таким образом, следующей задачей является построение математической модели процесса бурения шарошечным доло­том в такой форме, которая позволяла бы непосредственно вы­числять величину Zmax — Структура модели в свою очередь определит необходимый комплекс лабораторных исследований по разрушению горных пород, необходимый для ее функциони­рования.

Комментарии запрещены.