Бурение грунтовых зондов, установка энергетических колодцев

Результаты расчета показателей бурового процесса, описы­ваемого предложенной моделью, в значительной степени зави­сят от структуры вводимых в нее экспериментальных характе­ристик сопротивления породы внедрению зубцов долота. По­мимо свойств горной породы на характеристики P(z) в извест­ной степени могут влиять методы ее получения и обработки. Как бы тщательно ни воспроизводились забойные условия з лабораторной установке, все же они не могут быть вполне адекватными. Обработка осциллограмм может быть произведе­на различными методами. Ввиду дисперсии механических свойств данной породы, осциллограммы, входящие в серию, по­лученные в данных условиях, не идентичны. Таким образом, встает вопрос, каким образом учесть это при введении исход­ных данных в модель.

Сравнительная оценка качества вводимой информации о разбуриваемой горной породе может быть сделана на основании изучения результатов расчета с различными вариантами исход­ных данных. Весьма важно при этом выяснить, насколько чувствительна модель к качеству исходной информации. Этот вопрос существен также и с точки зрения возможности прогно­за показателей бурения на основании анализа характеристик P{z) без использования математической модели.

Зависимости силы сопротивления породы от глубины внед­рения зубцов [кривые P(z)], полученные экспериментально для различных пород, несмотря на их казалось бы бесконечное мно­гообразие, имеют тем не менее в большинстве случаев сходный, скачкообразный характер. Поэтому при изучении их целесооб­разно характеризовать следующими простыми показателями: угол наклона кривой упругого прогиба породы; величины сил, при которых происходят последовательные скачки разрушения, величины сил, до которых падает сопротивление породы при ее активном разрушении зубцом долота, и величины углублений зубца, соответствующие экспериментальным значениям силы сопротивления.

Таким образом удобнее производить указанные выше оцен­ки. В качестве выходных показателей расчета были принять* величина максимального внедрения зубцов долота в породу Zmax и необходимый крутящий момент Мср. Приведенные ниже данные основаны на использовании в качестве базовой упро­щенной кривой P(z), полученной для мрамора «коелга» эта­лонным зубцом с площадкой контакта 10X1 мм.

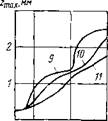
Для расчета была использована, кроме базовой кривой, еще серия характеристик, отличающихся друг от друга изменением координат различных элементов (пиков и впадин). Эта серия характеристик представлена на рис. 14.

Одновременно была сделана проверка влияния замены дей­ствительной кривой Р (z) ломаной. Для этого сравнивались варианты характеристик, приведенные на рис. 15. Они отлича­ются друг от друга различным способом соединения пиков и

Z, MM

Z, MM

Рис. 14. Схематические варианты зависимостей силы сопротивления поро­ды от глубины внедрения зубца

Р, тс Рис. 15. Аппроксимация зависи­мости силы сопротивления породы от глубины внедрения зубца ло­маной

впадин кривой, которые могут быть названы узловыми точка­ми характеристик P{z).

Расчеты показателей про­цесса бурения выполнены для варианта модели с тремя ци­линдрическими катками и по — лубесконечной колонны посто­янного сечения.

Для каждой из исследуе­мых кривых P(z) были прове­дены расчеты максимального углубления зубца долота в по­роду zmax и необходимого кру­тящего момента на долоте Afcp при следующих значениях осе­вой нагрузки: G = 5-f-30 тс.

Как было установлено расче­тами, углубление зубцов доло­та в породу и необходимый крутящий момент на долоте мало зависят от скорости вращения долота. Поэтому приводим результаты расчетов для условных пород только при скорости вращения п = 200 сб/мин.

Прежде всего необходимо дать количественную и качествен­ную оценки влияния характера последовательного соединения узловых точек на получаемые конечные результаты (см.

рис. 15). Расчеты показали, что зависимости величины углуб­
ления зубцов долота в породу и необходимого крутящего мо­мента на долоте от осевой нагрузки не зависят практически ни; качественно, ни количественно от принятого характера соедине­ния узловых точек. Это означает, что практически, не влияя на конечные результаты расчетов, можно заменять непрерыв­ную кривую P(z) соответствующей ломаной. Такая замена бывает весьма удобна при анализе, сравнении и использовании, этих характеристик горных пород. Применяя, по мере надобно­сти, такой вариант схематизации, в дальнейшем не будем спе­циально оговаривать корректность этой замены.

Затем была изучена группа условных кривых, которая отли­чается от базовой либо различными углами наклона упругого — вдавливания, либо силами, при которых происходят первый к второй скачки хрупкого разрушения.

	>7
А

zmax<MM

10

6,тс О

	>7
А	г}

МСр, кгс-м

50

10

20 G, mc

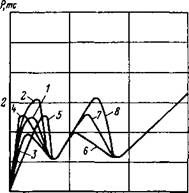
Рис. 16. Расчетные зависимости максимальной глубины внедрения зубца (а) и среднего кру­тящего момента (б) от осевой нагрузки для вариантов 1, 2, 3 Все три зависимости zmax(G) качественно аналогичны. С увеличением осевой нагрузки на долото углубление зубцов также увеличивается, хотя и существенно нелинейно. Эти кри­вые имеют участок интенсивного роста, соответствующего прео­долению сопротивления скачка разрушения горной породы. На остальных участках кривых возрастание углубления происходит гораздо менее интенсивно. Физически совершенно ясно, что ре­ализация интенсивного участка, т. е. объемного разрушения,, требует тем большей осевой нагрузки, чем выше расположен соответствующий скачок разрушения на кривой P(z). Поэтому

Кривые P{z) 1, 2, 3 (см. рис. 14, а) имеют общий угол на­клона первого упругого прогиба породы, но разную величину силы, при которой происходит первый скачок разрушения. Рас­четы максимального углубления зубцов долота в породу zmax и крутящего момента Мср, проведенные по этим кривым, показа­ли следующее (рис. 16).

зависимости zmax(G) для трех сравниваемых вариантов коли­чественно значительно отличаются друг от друга.

Нагрузки, необходимые для завершения объемного разру­шения, и особенно для его начала, в сильной степени зависят от высоты первого скачка, причем зависимость эта нелинейна. Поэтому следует предъявлять высокие требования к точности экспериментального определения этого основного элемента ха­рактеристики P(z). Можно сказать, что эта высота первого скачка динамической характеристики является основным фак­тором, определяющим разрушаемость данной горной породы.

Здесь необходимо указать, что расчет первого скачка объем­ного разрушения, выполненный на основании статической твер­дости по штампу, дает завышенные результаты для необходи­мой осевой нагрузки и поэтому может быть использован только для сугубо приблизительных оценок.

Теперь посмотрим, как влияет высота первого скачка раз­рушения, т. е. динамическая твердость породы, на величину крутящего момента, необходимого для перекатывания долота.

Графики зависимости крутящего момента на долоте от осе­вой нагрузки, полученные при расчете показателей бурения для условных кривых 1, 2, 3, повторяют зависимости 2max(G) толь­ко в области низких нагрузок (см. рис. 16,6). При увеличении осевой нагрузки до величины, необходимой для преодоления скачка разрушения самой твердой породы, все три кривые Zm&x(G) сливаются. Иначе происходит с величинами крутящих моментов на долоте. Чем больше сила, при которой происхо­дит первый скачок разрушения, тем выше поднимается кривая Mcp(G). Объясняется это следующим образом. Основная часть крутящего момента, необходимого для поворота шарошки, за­трачивается не на разрушение породы, ибо в этом случае сила сопротивления снижается, а на преодоление зоны упругого взаимодействия пары зубец — порода. Следовательно, при оди­наковой глубине внедрения зубцов в породу затрачиваемый крутящий момент тем больше, чем выше твердость породы по штампу, т. е. чем большую силу надо приложить для преодо­ления скачка разрушения.

Так как средний крутящий момент на долоте образуется суммированием мгновенных моментов, то полученное расхож­дение кривых Mcp(G) для условных кривых 1, 2, 3 физически вполне объяснимо. Здесь, однако, необходимо дать разъяснение. На первый взгляд сделанный вывод противоречит тому извест­ному факту, что при одинаковых нагрузках крутящий момент оказывается большим при бурении менее твердых пород. Это кажущееся противоречие. Дело в том, что промысловые дан­ные получаются чаще всего при недостаточных нагрузках. В этом случае, как видно из рис. 16,6, действительно, крутя­щий момент гораздо выше для более слабых пород. Зато при высоких нагрузках, обеспечивающих объемное разрушение,
картина меняется на противоположную. Этот анализ показы­вает существенное преимущество метода математического мо­делирования в прогнозировании показателей процесса бурения, ибо он позволяет исследовать физические причины формиро­вания показателей в широком диапазоне изменения режимных

параметров.

Анализ влияния динамической твердости породы на крутя­щий момент подтверждает важное значение этой характеристи­ки горных пород.

100

Кривые P(z) 1, 4, 5 (см. рис. 14, а) имеют различные углы наклона первого упругого прогиба породы, т. е. различную жесткость и одинаковую величину силы первого упругого скач­ка разрушения. Нетрудно заметить (рис. 17, а), что с увеличе-

J	г	i.. — .,

а, кгс-м

50

О 10

20 0,тс

Рис. 17. Расчетные зависимости максимальной глубины внедрения зубца (а) и среднего кру­тящего момента (б) от осевой нагрузки для вариантов 1, 4, 5

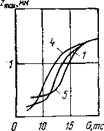
нием жесткости пары зубец — порода нагрузка на долото, необ­ходимая для преодоления первого скачка разрушения, умень­шается, однако далеко не так значительно, как при изменении силы первого упругого скачка. Кривые zmax(G) для трех рас­сматриваемых вариантов расположены близко друг к другу. Следовательно, фактор жесткости горной породы сравнительно слабо влияет на углубление зубцов долота при условии, что глубина разрушения, т. е. первые впадины кривых P{z) при разных жесткостях совпадают. Поэтому к точности эксперимен­тального определения угла наклона кривой P(z) на начальном участке не предъявляется жестких требований.

Однако с точки зрения крутящего момента дело обстоит несколько иначе. Для всех нагрузок кривая MCV(G) лежит тем выше, чем выше жесткость породы (рис. 17, б). Глуби­ны внедрения зубцов в породу 2гаах, начиная с нагрузки 20 тс, равны. Это различие становится явным, если рассмотреть из­менение крутящего момента, необходимого для поворота ша­рошки долота, во времени. Действительно, если для различных

6

	бУ[ / / 7 /У. м-‘
	‘ 8

МСр, кгс-м

100

50

10

	Y/	Т
	И-	)8
У	У

10

20 G. mc О

Рис. 18. Расчетные зависимости максималь­ной глубины внедрения зубца (а) и сред­него крутящего момента (б) от осевой на­грузки для вариантов б; 7; 8

пород при некоторой нагрузке наблюдается равное по величине углубление зубцов долота в породу, то величина необходимого крутящего момента будет определяться в основном характером упругого взаимодействия зубца долота с породой. Так как при одном и том же углублении зубца долота в породу сила реак- ции породы будет тем больше, чем выше жесткость породы, то и больший крутящий момент потребуется для преодоления уп- ругого сопротивления породы с большей жесткостью. Различие в крутящих моментах для бурения пород с раз- личной жесткостью достаточно велико, и с этой точки зрения приходится признать, что нужно определять достаточно надеж- но обе координаты первой узловой точки динамической харак- теристики горной породы P(z). Было исследовано также влияние величины силы, необходи- мой для осуществления второго скачка разрушения, на глубину внедрения зубцов долота. С этой целью были проведены расче- ты для условных кривых P(z) 3—6, 3—7, 3—8, представленных на рис. 14, а. Из полученных зависимостей (рис. 18, а) нетрудно заметить, что сила (на- грузка на долото), необ- ходимая для осуществле- ния двух скачков разру- шения, существенно воз- растает с увеличением высоты второго пика кри- вой P(z). Важно отме- тить также, что прираще- ние углубления далеко Z0 0,тс не пропорционально при- росту нагрузки на до- лото. Так, расчет для ус- ловной кривой 3—8 пока- зывает, что увеличение нагрузки в диапазоне 14—20 тс вызывает небольшой прирост углубления, в то время как увеличение нагрузки в пределах 20—22 тс приводит к увеличению углубления почти вдвое. Общий характер влия- ния силы второго скачка на величину углубления зубцов доло- та в горную породу вполне аналогичен влиянию силы первого скачка как качественно, так и количественно. То же можно ска- зать и о влиянии этого элемента динамической характеристики на необходимый крутящий момент (рис. 18, б). Представленные выше результаты расчетов показывают, что скачкообразный характер кривых P(z) приводит к весьма не- равномерному, сложному виду зависимостей углубления зубцов и крутящего момента от нагрузки. Правда, при этом нужно учитывать, что при проведении данного анализа была исполь- зована модель с тремя одинаковыми цилиндрическими шарош-

жами. При моделировании отдельных венцов долота несинхрон — жость контакта различных зубцов в значительной степени сгла­живает суммарные показатели и кривые zmax(G) и Mcp(G) ■становятся более плавными. Зато при таком простейшем моде­лировании резче проявляется физическая сущность изучаемого процесса.

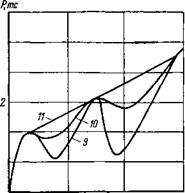
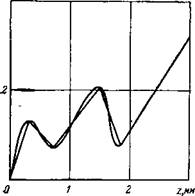
Если динамические характеристики Р (г) имеют более плав­ный, или даже монотонный характер, то и соответствующие кривые показателей также становятся более плавными. В этом смысле характеры кривых P(z) и зависимостей гтах(С) и. Mcp(G) тесно связаны между собой. Это хорошо видно при изу­чении результатов сравнительных расчетов по кривым 9, 10 и 11 (см. рис. 14,6). Влияние скачкообразности кривых P(z) на углубление зубцов и на крутящий момент практически одина­ково. Чем более резко выражена скачкообразность P(z), тем — больше становятся величины zmax и Мср почти во всем диапа­зоне исследуемых нагрузок на долото. Для плавной, пластич­ного характера, зависимости P(z) (кривая 11, рис. 14,6) изме­нение показателей zmax(G) и 34cp(G) также происходит плавно и монотонно (рис. 19).

Так как с увеличением дифференциального давления горные породы становятся более

пластичными и кривые а. б

F (z) приобретают более плавный характер, то проведенные расчеты для условных пород (кривые 9, 10, И) показывают

О 10 20 6,тс 0 10 20 0,тс Рис. 19. Расчетные зависимости максималь­ной глубины внедрения зубца (а) и сред­него крутящего момента (б) от осевой на­грузки для вариантов 9, 10, 11

также характер измене­ния зависимости углубле­ния зубцов долота в по­роду при увеличении глу­бины бурения.

Рассмотренные выше результаты расчета уг­лубления зубцов долота в породу и крутящих мо­ментов показывают, что величины сил, при которых происходят последовательные скач­ки разрушения, расстояния между ними и величины сил, до ко­торых падает сопротивление породы при ее активном разруше­нии зубцом долота, иными словами — узловые точки характе­ристики P(z), оказывают существенное влияние на получаемые конечные зависимости.

Напротив, ход кривой P(z) между условными точками су­щественной роли не играет.

На основании изложенного выше ясно, что предложенная математическая модель процесса бурения позволяет с учетом
механических свойств породы, определяемых кривой P(z)T предсказать ожидаемые результаты зависимостей величин уг­лубления зубцов долота в породу и необходимого крутящего момента на долоте от параметров режима для тех или иных условий бурения и конструкции долота.

При этом, если для выбранных условий бурения для какой — либо пары долото — порода установлены зависимости zmax(G) и Mcp(G), то они будут справедливы и для всякой другой по­роды, узловые точки которой совпадают с узловыми точками рассчитываемой кривой. Разумеется, для другого типоразмера долота количественные результаты будут иные, хотя качест­венно характеристики, по-видимому, останутся теми же.

Следует отметить, что в результате проведения широкой серии расчетов математической модели процесса бурения для различных условий бурения и пород накапливается материал, который в дальнейшем можно классифицировать по условиям бурения, применяемым долотам и кривым P{z). При этом уменьшается необходимость проведения расчетов для каждой вновь разбуриваемой породы.

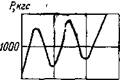
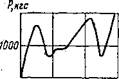
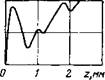
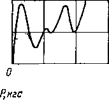
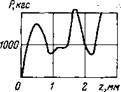
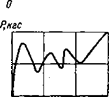
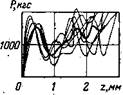
Из-за дисперсии механических свойств горных пород, даже таких сравнительно однородных, как мрамор, кривые P(z), по­лученные на одной поверхности образца, оказываются несколь­ко различными. Необходимо проверить, как скажется на ре­зультатах расчета с помощью математической модели это раз­личие при разных способах использования экспериментальных кривых. Наиболее правильным нам представляется подойти к этому вопросу следующим образом. При расчетах внедрения последовательно контактирующих зубцов необходимо исполь­зовать каждый раз одну из реальных кривых P(z), выбранную случайным способом из имеющегося экспериментального набо­ра. Такой способ соответствует действительному положению, при котором каждый зубец вступает в контакт с новым участ­ком забоя, где свойства горной породы могут несколько отли­чаться от предыдущих. На рис. 20 представлен такой экспери­ментальный набор, полученный для одной из разновидностей мрамора.

При расчете было получено значение максимального углуб­ления зубцов Zmax = 2,4 мм при нагрузке G = 20 тс. Для срав­нения были выполнены расчеты для каждой из эксперименталь­ных кривых, принятых за истинную для всех контактирующих зубцов. Совокупность расчетных значений углублений зубцоз Zmax выглядит при этом следующим образом: 2,7; 2,2; 2,4; 2,5; 2,7; 2,1; 2,5 мм. Средняя арифметическая этой совокупности составляет zmax = 2,4 мм. Как видим, с точностью до 0,1 мм результаты совпадают. Была также исследована возможность получения одной осредненной кривой из указанного экспери­ментального набора. Такая кривая представлена на том же рис. 20. При расчете по этой осредненной кривой углубление

Р, кгс

fjxzc

0 12 z, mm 0 12 z, mm

Л	/	Г)
I

1000

1000

1000

1 Z z, mm

1 Z z, mm

1000

2 z, mm

SHAPE * MERGEFORMAT

Рис. 20. Различные реализации эксперимен­тальных зависимостей силы сопротивления породы от глубины внедрения зубца

зубцов долота оказалось равным 2,6 мм. Разница с предыду­щими результатами составляет около 8%- Учитывая некоторое преимущество одной осредненной кривой по сравнению с набо­ром кривых, можно рекомендовать такой способ обработки экспериментальных результатов, однако с известной осторож­ностью.

Изложенный выше материал позволяет заключить, что ди­намические характеристики пород Р (z) для заданных условий бурения, с одной стороны, достаточно адекватно представляют данную горную породу, а с другой стороны, являются вполне консервативными, так что незначительные изменения в коорди­натах их элементов не меняют существенно результатов рас­четов. Это одновременно свидетельствует и об устойчивости выбранного нами метода решения системы уравнений матема­тической модели.

В заключение приведем еще один аспект возможного исполь­зования динамических кривых P{z). Речь идет об их исполь­зовании для некоторых вариантов классификации горных пород.

Можно считать общепринятым, что универсальной класси­фикации горных пород, пригодной для решения всех техниче­ских и технологических вопросов, в настоящее время не суще­ствует. Более того, можно высказать серьезные сомнения в том, возможна ли такая классификация вообще.

В различных отраслях промышленности с практическими целями используются несколько классификаций, предназначен­ных главным образом для характеристики сопротивляемости горных пород механическому разрушению. Для оценки механи­ческих свойств горных пород, разрушаемых при бурении сква­жин в нефтегазовой промышленности, применяется метод вдав­ливания штампа, предложенный проф. Л. А. Шрейнером. На базе этого метода существует классификация горных пород по твердости и условному коэффициенту пластичности.

Указанный метод и основанные на нем классификации в известной степени соответствуют рабочему процессу шарошеч­ного бурения, т. е. вдавливанию зубцов долота в поверхность забоя. Однако опыт показывает, что между буримостью горных пород и упомянутыми классификациями надежная корреляция отсутствует. Причин такого несоответствия несколько. Главные заключаются в том, что скорость внедрения штампа на несколь­ко порядков ниже скорости фактического внедрения зубца до­лота, с чем связано различие механизма разрушения и его ко­личественных характеристик. Кроме того, весьма важные для разрушения процессы фильтрации в породу буровой жидкости, происходящие во времени, существенным образом зависят от скорости взаимодействия инструмента с забоем.

Кривые P(z) могут быть использованы с целью классифи­кации горных пород в нескольких аспектах и прежде всего для классификации по буримости, принцип которой состоит в сле­дующем. Математическая модель бурения позволяет по экспе­риментальной кривой P(z) вычислить механическую скорость бурения для заданной конструкции долота и для любой ком­бинации режимных параметров. Если задаться долотом стан­дартизованного размера и конструкции, а также некоторыми стандартными режимными параметрами (нагрузкой и ско­ростью вращения), то каждой кривой P(z) будет однозначно соответствовать определенная механическая скорость бурения, которая и может быть использована в качестве классификаци­онного признака.

Выше было указано, что кривая P(z) может быть охаракте­ризована некоторым количеством параметров, определяющих ее узловые точки.

Если принять, что количество необходимых параметров п, то путем соответствующих расчетов на ЭВМ можно построить в л-мерном фазовом пространстве серию поверхностей v — const и установить однозначное соответствие между каждым набором указанных параметров и механической скоростью.

Практически это может быть сделано путем построения спе­циальных таблиц и номограмм, с помощью которых можно для каждой горной породы, получив и обработав ее кривую P(z), определить механическую скорость в стандартных условиях без предварительных расчетов.

Другим возможным аспектом использования кривых P(z) может быть построение классификаций по динамической твер­дости. В качестве классификационного признака здесь берется величина силы сопротивления при первом скачке разруше­ния Pi. В принципе эта классификация аналогична известной классификации по вдавливанию штампа, но она учитывает спе­цифические свойства горных пород, проявляющиеся при дина­мическом разрушении.

Сравнение динамических и статических шкал позволит раз­делить породы на классы по признаку влияния на процесс раз­рушения скорости механического воздействия.

Наконец, имеется одна возможность использования кривых P(z) для классификации горных пород по удельной энергоем­кости разрушения. В самом деле, площадь’ под кривой пред­ставляет собой работу разрушения. Задаваясь стандартной ве­личиной внедрения зубца и определяя каждый раз соответст­вующий объем разрушенной породы, можно составить класси­фикационную шкалу по признаку удельной энергоемкости.

Все сказанное выше свидетельствует о том, что кривые Р(г) являются в значительной степени универсальными харак­теристиками, которые могут быть использованы для построения различных классификационных систем, как перечисленных, так и некоторых других. Поэтому можно считать, что получение кривых P(z) должно быть одним из основных методов изучения разрушения горных пород механическими способами.

В заключение отметим, что оборудование, необходимое для получения кривых P(z), не сложнее обычного стандартного оборудования, применяемого при механических испытаниях ма­териалов.

Комментарии запрещены.