Бурение грунтовых зондов, установка энергетических колодцев

Согласно установившейся традиции понятие «режим буре­ния» включает в себя осевую нагрузку на долото, скорость его — вращения, количество и качество промывочного раствора. При отсутствии терминологического ГОСТа, однако, возможно про­извольно расширять или сужать понятие «режима бурения». Однако приведенная выше расшифровка не вполне соответст­вует сегодняшнему пониманию бурового процесса и неудобна при решении проблемы выбора так называемых «оптимальных режимов бурения». В самом деле, если понимать под «опти­мальным» такой режим, который обеспечивает достижение экстремального значения оптимизируемого показателя бурения» то следует указать набор количественных параметров этого режима. Это весьма затруднительно сделать в отношении ха­рактеристик, связанных с движением и функциями промывоч­ной жидкости. Полагаем, что гидравлическая программа буре­ния есть слишком сложный самостоятельный вопрос, чтобы включать его решение в задачу выбора оптимального режима. При проектировании гидравлической программы приходится иметь дело, по крайней мере, с тремя различными и противо­речащими друг другу функциями системы промывки — очисткой забоя и выносом шлама на поверхность, поддержанием задан­ного состояния стенок скважины и транспортом энергии, необ­ходимой для вращения забойного двигателя. Этот факт нахо­дит свое отражение уже в том, что в рапорте бурового мастера фиксируется свыше 10 количественных показателей» относящихся к системе промывки. Пытаться решить подобную многофакторную оптимальную задачу вероятно не представ­ляется возможным. Гораздо удобнее поставить вопрос иначе — определять оптимальную комбинацию осевой нагрузки и ско­рости вращения долота для заданных условий промывки. Это, впрочем, не исключает того, что поиски этой комбинации вы­полняются при различных вариантах программы промывки, допускаемых ограничениями, накладываемыми потребностями поддержания определенного состояния стенок скважины и при­вода забойного двигателя. При этом задача ставится точно так же, как и в отношении типа долота,— сравниваются показа­тели работы нескольких типов долот, выбираемых априори для разбуривания данной породы, но сравнение это должно быть сделано при оптимальной комбинации осевой нагрузки и скорости вращения для каждого долота. Таким образом, удоб­нее и целесообразнее включать в понятие «режим бурения» только два указанных фактора, рассматривая их при этом как независимые друг от друга.

Прежде чем перейти к обсуждению способа установления оптимальной комбинации пары режимных параметров: осевой нагрузки на долото G и скорости его вращения п — следует обсудить еще один немаловажный вопрос. Речь идет о том, должны ли оптимальные значения Gan быть функциями вре­мени. Альтернатива, таким образом, заключается в том, нужно ли стремиться изменять параметры режима по некоторой про­грамме, стремясь поддерживать их оптимальными в каждый момент времени, или целесообразнее сохранять их постоянны­ми во время бурения, пренебрегая неизбежными отклонениями режима бурения от истинного оптимума. Совершенно очевид­но, что в продолжение работы одного долота могут изменяться механические свойства горных пород и условия взаимодействия долота с забоем, например образовываться и исчезать рейка или ухабы. Кроме того, происходит износ или поломка зубцов долота, а также износ опор, который, в свою очередь, влияет на динамические характеристики буровой системы.

Можно представить себе специальные устройства, которые будут осуществлять непрерывный поиск оптимальной комбина­ции параметров с учетом ограничений, накладываемых приме­няемыми техническими средствами. Подобные устройства для прогнозирования результатов бурения должны использовать некоторые предположения о взаимосвязи между скоростью проходки и интенсивностью износа, с одной стороны, и интег­ральными показателями работы долота, такими, как проходка, рейсовая скорость и стоимость 1 м проходки, с другой. Иными словами, требуется использовать эмпирические уравнения про­цесса бурения, для чего указанное управляющее устройство должно располагать специализированной вычислительной ма­шиной, хотя бы и не очень сложной.

Нетрудно предсказать, что использование подобных уст­ройств в обычном эксплуатационном бурении вряд ли окажет­ся экономически и технически целесообразным.

У системы оперативного управления процессом бурения су­ществует еще один органический недостаток. Она неизбежно приспособлена к определенному способу бурения. Так, напри­мер, можно реализовать поиск оптимальной нагрузки на доло­то при турбинном бурении, так как при заданном расходе про­мывочной жидкости совокупность достигаемых режимов явля­
ется линией, но не областью. Однако это гораздо труднее сде­лать при роторном способе, поскольку неизвестно, при какой скорости вращения долота искать оптимальную нагрузку. Поиск в области требует возможности непрерывного изменения обоих регулируемых режимных параметров. По нашему мне­нию, оперативная система выбора оптимальных параметров мо­жет с успехом использоваться в некоторых специальных случа­ях, например при проводке опорно-технологических скважин для уточнения проектных режимных параметров и т. п.

Однако в общем случае бурение должно выполняться при постоянных параметрах G и п, в которые могут, конечно, вно­ситься оперативные коррективы, но при исключительных об­стоятельствах и по решению ответственных лиц, непосредствен­но руководящих бурением. Мы полагаем, что устройства, авто­матически поддерживающие постоянное значение G и п во время отработки долота, являются более простыми, надежны­ми, дешевыми и эффективными, чем система оперативного уп­равления бурением, действующая методом поиска. Итак, будем исходить из положения, что режим бурения должен быть ус­тановлен на стадии разработки проекта строительства сква­жины.

Каким же образом наиболее целесообразно подходить к проблеме выбора оптимального режима бурения? Вообще го­воря, оптимальный режим следует тем или иным способом ис­кать во всей области возможного изменения параметров п и G и, следовательно, необходимо эту область определить. Для этого можно воспользоваться техническими и энергетическими ограничениями, накладываемыми реально существующими ус­тановками, забойными двигателями и инструментом. Минималь­ная скорость вращения долота ограничивается характеристикой

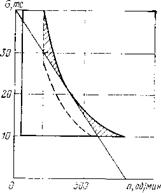
Рис. 67. Область определе­ния режимных параметров процесса бурения

роторного привода. Максимальная нагрузка в области роторного бу­рения определяется прочностью кон­струкции долота или продольной устойчивостью сжатого участка ко­лонны труб, поскольку мощность наземной силовой установки прак­тически ограничений не наклады­вает. Нижняя граница осевой на­грузки на долото при бурении по­род данного типа устанавливается, исходя из того, чтобы процесс раз­рушения породы не происходил пу­тем истирания. Что касается правой границы области, то поскольку она реализуется забойными двигателя­ми, то лимитируется мощностью, канализируемой с поверхности (рис.

67). Здесь нужно сделать некоторые пояснения. Рекомендации в отношении оптимального режима целесообразно давать в об­ласти п, G. Однако по необходимости некоторые построения и анализ приходится выполнять в поле п, М, где М — средний крутящий момент на долоте. В самом деле, мощность на валу, определяемую величиной Мп, очень удобно представлять в координатах п, М равнобочной гиперболой, не требующей для своего построения никаких специальных зависимостей. Кроме того, именно в этой системе координат принято представлять линейную характеристику турбины.

Между осевой нагрузкой на долото G и средним крутящим моментом М существует определенная зависимость, которая, впрочем, является различной для неодинаковых пород и в не­значительной степени зависит от скорости вращения долота. Функция M(G) может быть определена экспериментально и теоретически. В отечественной и зарубежной литературе можно найти достаточное количество материалов по этому вопросу. Таким образом, в большинстве случаев между нагрузкой на долото и крутящим моментом может быть установлено взаим­но-однозначное соответствие при заданных условиях бурения. Поскольку в некотором диапазоне изменения G ее взаимосвязь с М может считаться пропорциональной, то в грубом прибли­жении область определения параметров п, G подобна области п, М. Поэтому не будет серьезной ошибки, если на рис. 67 правую границу указанной области изобразить в виде кривой гиперболического типа, соответствующей той части мощности, канализированной с поверхности, которая может быть реали­зована на валу забойного двигателя. При этом не следует за­бывать, что поскольку к. п. д. двигателя не одинаков на разных режимах, то и правая граница области не может быть достиг­нута путем использования машины одного типа. Теоретически для каждой точки, а практически для каждого участка правой границы требуется машина с характеристикой, обеспечивающей на этом участке максимум к. п. д. Если же ограничиться одним типом забойного двигателя, например турбобуром, то гипербола должна быть заменена прямой, касательной к ней, и область изменения режимных параметров сократится на величину за­штрихованных участков (см. рис. 67). Так как верхняя граница области не зависит от ограничений подвода мощности, то она, вообще говоря, может не соединиться с гиперболой непосред­ственно. Оценочные расчеты показывают, что такое соединение имеет место лишь для достаточно крепких пород. Для средних и мягких пород тот же крутящий момент требуется при мень­шей осевой нагрузке, благодаря чему в координатах п, G линия предельной мощности опустится вниз (см. рис. 67). Итак, мож­но сказать, что область изменения режимных параметров в ко­ординатах п, G (или п, М) представляет собой криволинейную трапецию или трапецию, соединенную с прямоугольником. Каж­
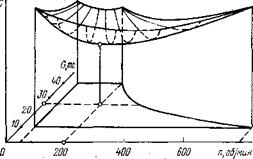
дой точке этой области соответствует единственное значение оптимизируемого показателя бурения, например стоимость 1 м проходки С. Совокупность этих значений внутри области обра­зует поверхность C=/(n, G) (рис. 68). Эта функция непрерыв­на вместе со своими производными и имеет один единственный минимум. Пара значений п и G, при которых достигается этот минимум, и является параметрами оптимального режима, т. е. Cmin —f(Пот> G0ut)-

Рис. 68. Поверхность стои­мостей 1 м проходки в об­ласти определения режим­ных параметров

Заметим, что обычно получаемые разными путями зависи­мости типа С(п) и C(G) являются сечениями поверхности С(п, G) плоскостями, параллельными координатным плоскос­тям п, С и G, С. Располагая набором зависимостей С(п) при разных G или C(G) при разных п, можно путем интерполяции восстановить соответствующий участок поверхности C(G).

Можно показать, что для построения поверхности C(G) до­статочно располагать значениями С* в сравнительно небольшом количестве базовых точек. Однако при этом точки п{, Gi долж­ны быть достаточно равномерно распределены по всей области изменения режимных параметров.

Разумеется, все сказанное выше относится не только к стоимости 1 м проходки С, но и к любому оптимизируемому показателю, например к рейсовой скорости ир.

Математическая модель процесса бурения при использова­нии эмпирических уравнений износа долот позволяет для каж­дой пары «долото •— порода» при заданных условиях бурения рассчитать зависимости типа C = f(G, п) в широком диапазоне варьирования режимных параметров. Кроме того, она дает воз­можность определить необходимую для целей оптимизации за­висимость между осевой нагрузкой на долото G и средним кру­тящим моментом М, т. е. функцию M(G).

Чтобы практически использовать такие зависимости, удобно строить так называемые режимные поля. Режимное поле пред­ставляет собой совокупность изолиний типа С = const ИЛИ 1’р = = const, построенных в координатах п, G. Такая совокупность

изолиний представляет собой набор проекций сечений по — В, тс верхности C = f(n, G) парал­лельными плоскостями С =

=const на координатную плоскость (п, G). На jq

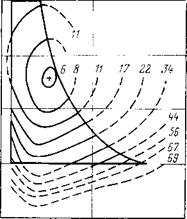
рис. 69 представлено поле сто­имостей 1 м проходки, рассчи­танных по математической мо­дели процесса бурения с не — 20 пользованием эмпирических уравнений износа долота. Ре­жимное поле позволяет легко найти искомые значения /г0пт 10 и Gопт, обеспечивающие дости­жение Cmm. Однако значение его этим не ограничивается.

Оно дает возможность опреде­лить, к каким последствиям ^ п, аВ/мин

может привести отклонение

режимных параметров от оп — Рис — ?9- Изолинии постоянных стои — 1 v ь мостеи 1 м проходки в области оп-

ТИМЗЛЬНЫХ значении В ТОМ или ределения режимных параметров ином направлении и, следова­тельно, установить не только точку, но и область оптимальных режимов, что весьма важно ввиду трудности поддержания по­стоянной нагрузки и скорости вращения долота, особенно в турбинном бурении. Определив область оптимальных режимов внутри области изменения режимных параметров, можно обо­снованно выбрать способ бурения и с учетом его особенностей дать необходимые режимно-технологические рекомендации.

Область оптимальных режимов, ограниченная некоторой изолинией, является в то же время и областью допустимых от­клонений оптимизируемого показателя от экстремального зна­чения. Она тем обширнее, чем менее жесткие требования предъ­являются к поддержанию оптимального режима. Можно ут­верждать, что внутри такой области отклонение оптимизируе­мого показателя бурения от экстремума не превысит заданной величины.

Весьма существенно, что такой метод позволяет добиться одновременной оптимизации по двум показателям, если в этом есть практическая необходимость, например, поддерживать ми­нимум стоимости при максимуме рейсовой скорости. Разумеет­ся, оба показателя достигают своих значений с определенной логрешностью. Для этого достаточно установить область пере­сечения оптимальных областей C = Cmln+AC и ор = ортах—Аор.

Пересечение областей гарантирует одновременное достиже­ние СШщ и Op с погрешностями, заведомо не превосходящими заданные величины А С и Аор.

Рассмотрение области изменения режимных параметров по­казывает, что было бы неверным ставить вопрос о приоритете какого-либо одного способа бурения. Вне всякого сомнения, свои области использования имеются у ротора, высокооборот — кого турбобура, низкооборотного турбобура, винтового двига­теля и электробура. Однако это отнюдь не предрешает удель­ный вес применения каждого из способов. В освоенных районах практический опыт позволяет постепенно решить вопрос о приоритете какого-либо способа, но для разработки новых мес­торождений должна быть проведена серьезная работа по пред­варительному определению области оптимальных режимов, ко­торая позволит составить научно обоснованные проекты строительства скважин.

Для целей практического использования способ графичес­кого определения оптимальных режимов бурения, основанный на построении линий постоянных стоимостей, представляется излишне трудоемким. Кроме того, приходится заранее рассчи­тывать всю сетку точек, в результате чего области, не пред­ставляющие существенного интереса для оптимизации, просчи­тываются с той же частотой, что и более важные участки сетки. Можно предложить метод нахождения оптимума с минималь­ным количеством расчетов с тем, чтобы более подробно иссле­довать лишь окрестность оптимальной точки. Для нахождения точки поля, в которой стоимость 1 м проходки достигает ми­нимального значения, используем метод покоординатного спуска [7], позволяющий свести многомерную задачу к одно­мерной.

Переменная стоимость С представляет собой функцию двух переменных п и G. Для удобства дальнейшего изложения обоз­начим х=п, y—G.

Задаемся первым приближением С(х0, г/о), которое следует выбрать в режимном поле, либо исходя из практического опы­та, либо произвольно. Затем при фиксированном значении од­ной из переменных, например г/, отыскивается значение х—хи при котором достигается infC(x, у0). Аналогично определяем значение у — у, при котором достигается inf С (хи у). Таким об­разом, осуществляется переход от исходной точки (х0, г/0) к точке (хи у). Процесс циклически повторяется столько раз,, сколько необходимо, чтобы выполнить неравенство

I С (xk> Уа) — С (Хк-и у к-1) I < е. (6.10)

При отыскании минимума функции С таким способом возни­кает проблема минимизации функции одной переменной.

При минимизации функции С(х, у) на каждой ступени этого расчета пользуются параболической аппроксимацией по трем заданным точкам. Такой способ обеспечивает достаточно на­дежное пошаговое движение точки к оптимуму.

Приведенный способ позволяет определить координаты точ­ки в режимном поле, которым соответствует экстремальное зна­чение оптимизируемого показателя.

Как было показано выше, кроме определения непосредст­венно оптимальной точки важно построить режимное поле С = = const. Для этого область варьирования режимных парамет­ров покрывается расчетной прямоугольной сеткой, которую це­лесообразно выбирать более густой в непосредственной окрест­ности оптимальной точки. Дело в том, что предлагаемый ниже метод линейной интерполяции при построении режимного поля дает тем более точные результаты, чем гуще расчетная сетка. В узлах сетки с помощью математической модели вычисляются значения стоимости С. После этого дополнительная программа позволяет вычислить координаты ряда точек для каждой изо­линии С = const. _

(6.11)

Построим изолинию C = Cmin + AC. При фиксированном зна­чении одной из координат оптимальной точки, например yh, ищем те узловые точки сетки (х, yh) и (х + Дх, yh), между ко­торыми лежит точка режимного поля, в котором С=С. Очевид­но, они должны удовлетворять соотношению

[С — С (х, yk)] [С — С (х + Дх, yk)] < 0.

Координату х искомой точки вычисляем следующим обра­зом:

(6.12>

Ах[С-С(х, yk)}

Меняя значения у и повторяя этот расчет, можно получить координаты точек режимного поля, для которых С —С. Чтобы увеличить точность построения изолиний, аналогичным образом определяем соответствующие точки на вертикальных линиях сетки. Меняя значение С, строим полное режимное поле С— — const.

Весь цикл расчетов вплоть до определения оптимальной точки и построения режимного поля для данной пары «долото— порода» выполняется с помощью единой комплексной програм­мы на ЭВМ.

Подобные расчеты выполняются для предварительно отоб­ранных типов долот. Таким образом, появляется возможность выбрать оптимальный тип инструмента для разбуривания данной породы при сравнении их эффективности в условиях, когда каждое сравниваемое долото используется при оптимальном для него режиме. Это исключительно важное обстоятельство становится возможным только благодаря использованию метода математического моделирования, не ограниченного областью варьирования режимных параметров.

В случае, если расчетная область оптимальных режимных параметров по каким-либо причинам не может быть реализо­вана, приходится сталкиваться с известной неопределенностью,

заключающейся в том, что одно и то же значение показателя эффективности достигается при множестве различных сочетаний п и G вдоль изолиний ир = const или С = const.

Для того, чтобы однозначно решить этот вопрос, целесооб­разно провести анализ режимного поля, построенного в коор­динатах п, М. В самом деле, в этих координатах линии постоян­ной мощности являются гиперболами Mn = const. На каждой изолинии, например С=const, можно найти точку, соответст­вующую минимальному значению Мп, т. е. минимальной мощ­ности. В этой точке изолиния С — const касается гиперболы Mn = const. Соединяя такие точки, принадлежащие разным изолиниям, получаем область наилучших режимов, соответст­вующих изменяемой мощности, подводимой к забою.

В случае турбинного бурения на режимное поле в коорди­натах пМ удобно нанести характеристику турбобура. При этом становится очевидным, в какой области характеристики целе­сообразно работать и к каким последствиям приведет отклоне­ние от этой области, в частности, недогрузка долота.

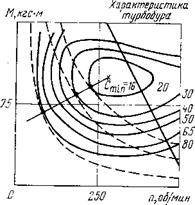
На рис. 70 приведен, в качестве примера, один из вариантов расчетного режимного поля С = const. Легко видеть, что при

Рис. 70. Расчетное поле стоимо­стей 1 м проходки

увеличении располагаемой мощности следует увеличивать крутящий момент и скорость вращения долота до опреде­ленного предела, при котором достигается минимум стоимо­сти 1 м проходки. Дальнейшее форсирование режима приво­дит к обратному результату. При работе с турбобуром, ха­рактеристика которого приве­дена на рис. 70, приближение к холостому режиму ведет к резкому увеличению стоимо­сти. Очевидно также, что, на­пример, при скорости враще­ния порядка 100 об/мин уве­личение крутящего момента и, следовательно, осевой нагруз­ки мало изменяет стоимостные показатели. Поэтому имеет смысл увеличивать нагрузку, так как при этом, естественно, возрастут технические показатели при неизменной стоимости 1 м проходки.

Приведенный пример, конечно, не претендует ни на какие количественные рекомендации, так как он рассчитан для одного конкретного варианта бурения. Он является лишь иллюстраци­ей метода анализа режимного поля с целью определения ситуа­ции с выбором способа и режима бурения.

Для функционирования математической модели процесса бу­рения, как уже отмечалось выше, необходимо лабораторное ис­следование кернов с целью получения механических характе­ристик разбуриваемых горных пород. Поэтому следует опреде­лить систему отбора кернов, которая позволила бы получить расчетные зависимости показателей бурения для участка разре­за протяженностью не менее величины средней проходки на долото, фиксируемой на данной глубине. Такая постановка за­дачи исходит из предположения, что проектный режим выдер­живается неизменным и оперативные средства управления при этом использовать экономически нецелесообразно.

При возможности сплошного отбора керна по стволу можно было бы представить себе следующую идеализированную схему обработки кернового материала. Прежде всего следовало бы произвести петрографический анализ горных пород, входящих в разрез, составить детальную литологическую колонку, изгото­вить образцы, представляющие все подразделения этой колон­ки, и произвести их лабораторные испытания. В соответствии с полученными механическими характеристиками породы могут быть разделены на статистически различимые группы и каждая группа представлена набором характеристик, используемых при расчетах математической модели. Таким образом составля­ется расчетная колонка, или, иными словами, модель разреза.

Далее следовало бы произвести расчеты в следующем по­рядке. Для верхней породы рассматриваемого разреза или участка разреза определяется оптимальный режим бурения, тии долота и соответствующая проходка на рейс. Затем рассчиты­ваются оптимальные параметры для всех подразделений модели разреза, попадающих в указанный рейс. Решение оптимальной задачи сводится к сравнению показателей процесса бурения для различных технологических вариантов. Поясним сказанное на простейшем примере. Предположим, что в проходку, вычислен­ную по верхней породе, входит еще одна статистически разли­чимая разновидность породы. Тогда сравниваются показатели бурения в двух вариантах, из которых один является оптималь­ным для первой породы, а второй — для другой. Для выбран­ного оптимального варианта просчитывается уточненное зна­чение величины проходки на долото. Затем расчет повторяется для следующего рейса. Аналогично решается оптимальная за­дача, если долото проходит не две, а три или более статисти­чески различимые породы. В результате может быть получен расчетный вариант выбора долот и режима бурения для всего рассматриваемого разреза.

На основании изложенного выше можно представить полную схему выполнения всей последовательности расчетов. Однако практически трудно рассчитывать на получение полного комп­лекта кернового материала с помощью сплошного отбора, не говоря уже о значительной трудоемкости петрографического анализа и производства большого количества лабораторных испытаний и расчетов.

Поэтому для составления программы отбора кернов необхо­дима предварительная разбивка разреза месторождения на интервалы на основе выбранного критерия. Например, можно осуществлять выбор керна на основании разбивки разреза на интервалы сходной буримости по технологическим параметрам. Такой способ удобен тем, что количество интервалов по сква­жине обычно бывает сравнительно невелико и потребность в керновом материале и лабораторных испытаниях ограничена. Этот способ, однако, имеет существенные недостатки, так как в пределах каждого интервала сходной буримости могут встре­чаться литологически различные породы и границы участков от­бора керна внутри интервала ничем не регламентированы. Можно выбрать промежуточный вариант, который хотя и не предусматривает сплошного отбора керна, однако основан на использовании литологической колонки внутри каждого интер­вала сходной буримости. Эта колонка может быть составлена на основании информации, которой располагают геологическая и геофизическая службы. Кроме того, можно использовать для этой цели лабораторный анализ шлама при условии организа­ции его систематического отбора. При этом по каждому интер­валу сходной буримости могут быть отобраны керны наиболее представительных разностей.

Наконец, в случае отсутствия всяких систематических сведе­ний по разрезу может быть использован любой имеющийся керновый материал, удовлетворяющий требованиям лаборатор­ных испытаний. На основании его обработки и соответствую­щих расчетов могут быть выбраны долота и оптимальные режи­мы бурения в ряде точек по стволу скважины. Эти точки прини­маются за базовые и служат основой для составления програм­мы приближенного выбора технологических вариантов бурения, подлежащих, разумеется, дальнейшей корректировке.

Комментарии запрещены.