Бурение грунтовых зондов, установка энергетических колодцев

Models which behave according to the Bingham plastic model will not flow until the applied shear stress, t exceeds a certain minimum shear stress value known as the yield point, ty but after the yield point has been exceeded, changes in shear stress are directly proportional to changes in shear rate, with the constant of proportionality being called the plastic viscosity, ц In reality the fluid will flow when the gel strength of the fluid has been exceeded. The yield point defined in the Bingham model is in fact an extrapolation of the linear relationship between stress and shear rate at medium to high shear rates and as such describes the dynamic yield of the fluid. The gel strength represents the shear stress to shear rate behaviour of the fluid at near zero shearing conditions. This model can be used to represent a Newtonian fluid when the yield strength is equal to zero (ty = 0). In this case the plastic viscosity is equal to the Newtonian viscosity. The above equation is only valid for laminar flow.

2.5.3 Power Law Model

The power-law model is defined by the following mathematical model: t = Kgn

Equation 5 Shear Stress to Shear Rate Relationship for Power Law Fluids

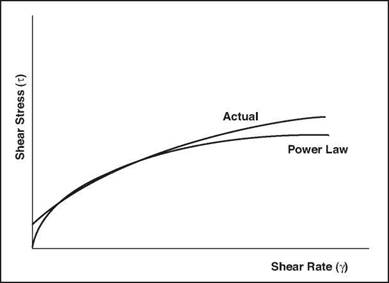
A graphical representation of this model is shown in Figure 10. Like the Bingham plastic fluid, the power-law fluid requires two parameters for its characterisation. However, the power-law model can be used to represent a pseudoplastic fluid (n < 1), a Newtonian fluid (n = 1), or a dilatant fluid (n > 1). The above is only valid for laminar flow.

This model is the best approximation for the behaviour of Polymer based fluids. The parameter K is usually called the consistency index of the fluid, and the parameter n is usually called either the power-law exponent or the non-Newtonian index. The deviation of the dimensionless flow-behaviour index from unity characterises the degree to which the fluid behaviour is non-Newtonian.

Parameter c. g.s Units Field Units

Viscosity lpoise (100 cp,1 dyne-s/cm2, 1/479 lbf-s/sq ft.

1 g/cm. s)

Yield Point 1 dyne/cm2 1/4.79 lbf/100 sq. ft.

Consistency Index, K 1 dyne-sn/cm2 (1 g/cm. s2-n) 1/479 lbf-sn/sq. ft.

Table 1 Rheological Parameters and Units

3. FRiCTiONAL PRESSURE DROP iN PiPES AND ANNULI

when attempting to quantify the pressure losses inside the drillstring and in the annulus it is worth considering the following matrix:

An equation will be required to describe each of the elements in the above matrix. The following section of this chapter will therefore present the equations which have been developed for each of these set of conditions.

Комментарии запрещены.