СОВРЕМЕННЫЕ ПРЕДСТАВЛЕНИЯ О ТЕОРИИ РАЗРУШЕНИЯ ГОРНЫХ ПОРОД ПРИ РАЗЛИЧНЫХ СПОСОБАХ БУРЕНИЯ
СОВРЕМЕННЫЕ ПРЕДСТАВЛЕНИЯ О ТЕОРИИ РАЗРУШЕНИЯ ГОРНЫХ ПОРОД ПРИ РАЗЛИЧНЫХ СПОСОБАХ БУРЕНИЯ
Разрушение породы является основной операцией при бурении скважин. В результате силового воздействия породоразрушающего инструмента в породе возникает упругое напряженное состояние. С увеличением нагрузки напряжения в горной породе возрастают и в итоге достигают предельного значения. Дальнейшее повышение нагрузки приведет к разрушению породы либо к пластической деформации. Однако изменение напряжений во времени и характер протекания деформации во многом зависит от генезиса и кристаллического строения породы. Все горные породы по характеру изменения деформации при внедрении твердого тела (штампа) делятся на следующие группы: хрупкие, пластично-хрупкие, упругопластичные, высокопластичные.
Распределение напряжений в горной породе также зависит от геометрической формы резца, которая может быть представлена в виде цилиндра, сферы, клина или призмы с плоскостью, ограничивающей упругое пространство. Процесс перераспределения напряжений по поверхности контакта резца с породой и переход одного вида деформации в другой с увеличением нагрузки очень сложен. Эти вопросы рассматриваются в работах А. А. Шрейнера, Б. В. Байдюка, H. H. Павловой, P. M. Эйгелеса, Е. Ф. Эпштейна, Н. И. Любимова и др.
Механизм разрушения горной породы с применением породоразрушающего инструмента обычно моделируется при вдавливании жесткого индентора (штампа) той или иной формы в образец породы, именуемой упругим полупространством.
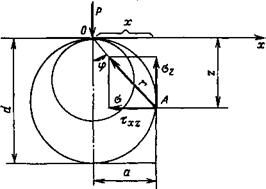
Согласно теории упругости под действием сосредоточенной силы в упругом полупространстве возникают напряжения, значения которых определяются в задаче Буссинеска. С помощью этой задачи можно найти положение поверхностей,
|
3 Р = -— г 2* |
|
’(а |
|
2 , „2)-2 |
|
+ г |
|
|
|
|
|
|
|
|
а2 + г2)’ |
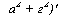 21
21
|
(4.2) |
![]() =—- 02 I
=—- 02 I
2 п х
Полное напряжение, действующее в точке А и направленное к месту приложения силы Р, будет составлять
|
= л/ст |
|
2+т2 = |
|
3Р СО$ (Р 2я г2 |
|
|
На оси симметрии Ог (при ср = 0) будут действовать нормальные напряжения ст*, стх, сту; которые определяют из следующих выражений:
з Р, л,ч
<** = -—; (4-4)
2 пг
Оу =о„ =^-^-{1-2ц), (4.5)
4 пг
где ц — коэффициент Пуассона.
Из последнего выражения следует, что на оси симметрии все напряжения сжимающие, что соответствует всестороннему сжатию.
На поверхности образца, т. е. при ф = — , имеем а2 = 0; ау = (1 — 2ц) Р
2 пг2
-0-2Ц) Р
2 пт2
Из равенства ау = — стх следует, что на поверхности полупространства имеет место чистый сдвиг.
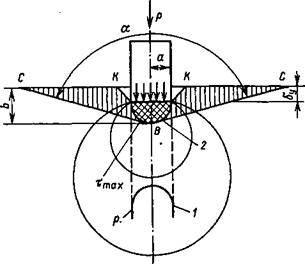
При вдавливании в горную породу цилиндрического штампа с плоским основанием вертикальное давление Р, действующее на штамп и заменяющее сосредоточенную Р в задаче Буссинеска, распределяется по кругу (рис. 4.2).
|
Рис. 4.2. Деформация хрупкой горной породы при вдавливании цилиндрического штампа с плоским основанием (по АЛ. Шрейнеру): 1 — распределение давления под штампом; 2 — распределение максимальных касательных напряжений (по изохроме). Разрушение горной породы при достижении конечной упругой деформации показано конусом СВС |
В этом случае давление под штампом распределяется неравномерно и определяется следующей формулой:
В центре штампа (х = 0) давление
|
Р
|
Здесь р(х) — функция распределения давления по плоскости контура штампа; Р — сила, действующая на штамп; а — радиус штампа; х — расстояние от оси симметрии, на котором действует сила Р.
При вдавливании абсолютно жесткого цилиндрического штампа значение абсолютной упругой деформации породы определяется выражением:
|
|
|
5 |
![]()
|
У |
![]() (4.7)
(4.7)
При вдавливании штампа максимальные касательные напряжения ттах, имеющие одни и те же значения, расположены на окружностях (изохромах), проходящие через края штампа (см. рис. 4.2).
Наибольшее максимальное касательное напряжение находится на направлении оси штампа, на глубине г = Ь — — 0,637а. Численное значение этого напряжения т0тах = 0,33; для коэффициента Пуассона ц = 0,3. При г = 0, т0тах = 0,1р.
Глубина Ь, на которой возникает т0шаХ, получила название критической, так как на этой глубине напряжения превышают предел прочности породы и вызывают появление трещин, которые выходят на поверхность. Этот процесс сопровождается крупным выколом породы по плоскости, расположенный под углом а, несколько большим 120°. В зависимости от геометрической формы соприкасающихся упругих тел, меняются значения критической глубины И величины Тошах-
Разрушение горной породы под индентором при достижении конечной упругой деформации будет происходить по конусу, который имеет вертикальное сечение в виде треугольника свс.
Герц установил, что при контакте двух цилиндров по площадке с шириной 2а критическая точка Ь находится на глубине 0,78а, причем
где Р — нагрузка на единицу длины полоски.
При контакте шара с плоской поверхностью, по данным А. П. Динника, наибольшее касательное напряжение Топих = = 0,31 Ртах возникает на глубине Ь = 0,47а. В данном случае а — радиус круга контакта, a pmax — максимальное давление. При внедрении штампа большей длины в горную породу (М. Садовский, Л. Надин и др.) максимальное касательное напряжение Тот« = р/71 возникает на глубине Ь = а, где р — равномерно распределенное давление; а — половина ширины штампа.
Таким образом, процесс разрушения горных пород под действием штампа или резца протекает очень сложно и зависит от механических свойств пород, величины прилагаемой нагрузки и геометрической формы индентора.