Бурение грунтовых зондов, установка энергетических колодцев

Одна из первых аналитических зависимостей была предложена Б. И. Есьманом. В основу вывода была положена методика И. А. Парного, примененная нм для решения задачи о внутреннем подогреве горизонтального трубопровода, с изменением способа нахождения постоянных интегрирования. Однако полученные таким методом окончательные выражения оказались громоздкими и не при­годными для практического использования.

В дальнейшем подобную же задачу решали А. М. Погорельский и И. А. Кулиев [651. Эти авторы, рассматривая для обобщения задачи случаи бурения электробуром, принимают за исходные сле­дующие условия.

1. Температура пород изменяется по линейному закону.

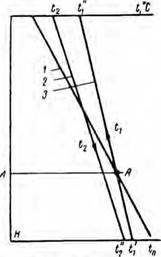
2. Восходящий поток промывочной жидкости на участке ниже нейтральной липни.4 — Л (рис. 29) играет роль одновременно и нагреваемого тела и греющего теплоносителя, а на участке выше этой линии он является только греющим теплоносителем.

3. Температура восходящего потока промывочной жидкости достигает своего максимума t’ на забое скважины, имеющей глу — бшгу II.

4. В нисходящем потоке температура промывочной жидкости <2 дополнительно повышается в результате частичного преобразования

электрической энергии (в то ко подводе и забойном электродвигателе), механической энергии (работа долота) и гидравлической энергии (наличие гидравлических сопротивлений) в энергию тепловую.

5. Процесс теплопередачи предполагается стационарным.

При таких условиях количество тепла, полученного нисходящим потоком жидкости от восходящего, может быть выражено форму­лой

Q — k’nH Дг, (VI.1)

где Дt — средняя логарифмическая разность температур между восходящим и нисходящим потоками:

A t

(it —12)—(t, — <2)

(VI. la)

In

и (J — температуры соответственно восходящего и нисходящего потоков на устье; t[ и — то же на забое; к’ — линейный коэффициент теплопе­редачи от восходящего потока к ни­сходящему:

1

к’ —•

(VI.16)

■ In ■

a, d

а2 dj

В этом уравнении а}, ои — коэффи­циенты теплоотдачи соответственно от нисходящего и восходящего потоков промывочной жидкости к поверхностям Рис. 29. Схема распределения бурильных труб в ккал/м2 — ч • °С; температуры в процессе бу — л л — внутренний и внешний диа — рення скважины. м^ры2 бурильных труб в. ч; Хс — ко-

1 то№ ВосхоздщайЯпотокПО" эффициент теплопроводности материала

бурильных труб в ккал/м • ч • °С. Уравнение теплового баланса для нисходящего потока записы­вается авторами [65] в виде

(VI.2)

где G — весовой расход глинистого раствора в кг! ч с — средняя весовая теплоемкость промывочной жидкости в ккал/кг • °С.

Здесь

+ ^ + (VI. 2а)

сумма количества тепла в нисходящем потоке жидкости, выдели­вшегося за счет внутренних источников, в ккал/ч. При этом

Ар""с

— тепло, выделившееся вследствие преобразования гидравлической энергии в тепловую; Д(?2 = 860 ДИ7 — тепло, выделившееся из токо — подвода, находящегося внутри колонны бурильных труб; AQ3 — = 860 (W — ДИО — тепло, полученное в результате преобразова­ния электроэнергии, потребляемой электробуром при разрушении долотом породы; Д<?4 = ДG cata — тепло, вносимое разрушенной породой в нисходящий поток промывочной жидкости.

В указанных выше формулах: W — расход электроэнергии,

подводимой к токоподводу, в кет • ч; ДРУ — электрическая энер­гия, преобразованная в тепловую в токоподводе, в кет • ч; ДG — вес породы, разрушенной долотом на забое, в кг! ч сп — сред­няя теплоемкость породы, разрушенной на забое, в ккал/кг • °С;

— температура пласта в °С; Д рии — падение давления в нисходящем потоке жидкости, обусловленное наличием гидравли­ческих сопротивлений, в кг/м2; унп — объемный вес промывочной жидкости нисходящего потока в кГ/м3.

Температурный скачок t[ — t в потоке жидкости на забое обусловлен поступлением количества тепла Д(?3 — j — Д@4. В соответ­ствии с этим тепловой баланс на забое скважины

(VI.3)

GcC + Д<?3 + Л& = (С + Д G) cCHt[.

Подстановка в (VI.3) значений Д(?3, AQt при допущении ссм *=»

Q

и ‘ — я» 1,0 приводит к достаточно точному для практиче-

(J ~J~

ских расчетов выражению

(VI.4)

8e0(W-AIV) + AGcnt„

1 г~ с(б + ДС) *

в котором величина ДG может быть найдена по формуле

где D — диаметр скважины в at; vu — механическая скорость про­ходки в л/ч; уп — объемный вес породы на забое в кГ/м3.

При отсутствии работы забойного двигателя t[ среднеариф­метическая разность температур между нисходящим и восходящим потоками будет

При этом уравнение теплового баланса для нисходящего потока примет следующий вид:

из которого находят величину t“t. Однако учитывая, что температур­ное поле в бурящейся скважине не является достаточно стационар­ным, а расчетные значения к’ и Драп могут отклоняться от действи­тельных, авторы [65) считают необходимым окончательное
выражение для определения t"2 дополнить некоторым поправочным коэффициентом ф1ч который должен находиться из опыта. Таким образом, окончательное выражение для tn при отсутствии работы забойного двигателя принимает вид:

як П (<, tn) , 1 ^Pnii I /у |

2 Gc + 427c ■» I’ ( ‘

Для определения забойной температуры восходящего и нисходя­щего потоков в процессе непосредственного бурения авторы [651 предлагают следующую методику.

По уравнению (VI.4) определяют скачок температуры на забое t’j — t’z, зпая который и измерив па устье скважины температуры t'[ и t’2, по формуле (VI.1а) определяют величину At.

Далее в первом приближении находят значение к’ (полагая «к tu) из выражепия (VI.16). Зная А1 и к’, можно пайтн величину Q по формуле (VI. 1). Кроме того, по соответствующим формулам определяют составляющие AQU AQZ. Если все значения найдены, то искомую величину находят из выражения (VI.2), причем в окон­чательное выражение также вводится поправочный коэффициент ф2:

Ч = фа [<;4—^- (лЛ’Я At + 2 Д&)] • (VI. G)

По уравнению (VI.4) определяют величину /(:

, 800 (IV—ДУГ) — f — #„Im

h-h — 7ЩГЩ ■

Как указывают авторы названной работы, пределы изменений поправочных коэффициентов ф2 и ф, при различных условиях буре­ния будут определены дальнейшими исследованиями.

Более строгое решение этой же задачи принадлежит А. А. Афа­насьеву [5, 61, который исходит из условия, что изменение темпера­туры однофазного потока в общем случае обусловлено теплообменом с окружающей средой, внутренним теплообменом (необратимые превращения работы трения в тепло), работой потока в поле тяготе­ния и изменением кинетической энергии потока.

Для учета всех перечисленных факторов автор использует пред­ложенные Н. И. Белоконем уравнение I начала термодинамики по балансу рабочего тела

6Q* ~Gdi I AbW*, (VI.8)

выражение потенциальной работы

т * =- бL* 4- md (-f-) 4- mgdz (VI.9)

и основные принципы теории теплопередачи при переменных темпе­ратурах.

Принимая для условии бурящейся скважины

6i;,=o, d(-f-)=o

и учитывая, что

Q

т = —, di — cpdl — epDi dp,

А. Л. Афанасьев из выражений (VI.8) и (VI.9) получает следующие уравнения сохранения энергии восходящего и нисходящего потоков, учитывающих внешний теплообмен на участке dx:

kxndmi (x—t)dz = Gcpdt — GcD^dp-j — AG -%-dz, (VI.10) aa.-id2 (t — 0)riz = Gc dx — Gc Df, dp2 — AC —dz — kxndm, (r — t)dz.

V Sn

(VI.11)

В выражениях (VI.8) — (VI.11) приняты следующие обозначения: бQ * — внешний теплообмен (с окружающей средой); Л — термиче­ский эквивалент механической работы; бLe* — работа, переданная телам внешней системы; бW* — потенциальная работа; т — рас­четная масса; g„ — стандартное ускорение (gn — 9,80665 м/сек2 в системе кг — кГ — м—сек, gH — 1 в системах СИ и СГС и т. д.); g — истинное ускорение притяжения; G — стандартный вес (сино­ним количества вещества), в рассматриваемом случае — расход циркулирующей жидкости; с — скорость потока; i — энтальпия потока; ср — истинная теплоемкость при постоянном давлении;

D. — коэффициент Джоуля — Томпсона; t — темиература нисхо­дящего потока; т — температура восходящего потока.

Для остальных величин нисходящего п восходящего потоков используются соответственно индексы 1 и 2: кх — коэффициент теплопередачи между потоками; аг — коэффициент теплоотдачи от стенки бурильной трубы к внутреннему потоку; dmi — среднее значение диаметра трубы (dm = dx +бг); dA — диаметр сечения нисходящего потока; 6j — толщина трубы; A. J — коэффициент тепло­проводности материала трубы; а2 — коэффициент теплоотдачи от внешнего потока к окружающим породам; а’ — коэффициент тепло­отдачи от внешнего потока к ограждающей стенке внутреннего по­тока; d2 — диаметр сечения внешнего потока; 9 — текущая темпе­ратура стенки внешней трубы (обсадной колонны; практически температура окружающих пород).

При этом

Определив из (VI.10) и (VI.11) значения т и dxldz и введя обо­значения

Gcp ~а" Gcp ~a*’

после пекоторых преобразований автор находит следующее диф­ференциальное уравнение для определения температуры нисходя­щего потока *:

“«15—“!««*-/(*). (VI.12)

где

/(*)-— («1 + дг) (*) — f а* ~ + Di. pl (z) + ayDi’Pt (z) —ягаа (0).

fen

Решение уравнения (VI.12) дается в виде выражения

TOC o "1-5" h z * I

I Во— . 2 Г — f /*- ® О “£) г ^ Jo

t ==• с, exp —z с2 exp — V~z + x sh — (z—

° (VI. 13)

Я = ]/ ai + 4a, aa, (VI. l3a)

где Ј — переменная интегрирования; при интегрировании по £ переменная z считается величиной фиксированной; сj и cg — кон­станты интегрирования, которые находятся из условия t = t0 при z = 0; tH = тн при z = Н.

Применительно к наиболее распространенному в практике слу­чаю, когда можно принять линейное распределение давлений и тем­пературы пластов с глубиной, решепие уравнения (VI. 13) значи­тельно упрощается и общие отношения зависимости температуры циркуляционного потока от глубины бурящейся скважины прини­мают вид:

‘ <VI14> (VI.15)

где

ml = D —ехр —|- ка, ехр ^ —“’Г") • (VI.14а)

д1 = В *=Ь ехр (- М ) + ка, ехр (- . (VI. 146)

1 Аналогичное дифференциальное уравнение получено я в работе (24, вы­ражение (1.18)]. Однако из-за допущенной в знаках ошибки при составлении баланса тепла оно неверно записано со знаком -(- перед вторым членом левой части уравнения.

£> =

(VI.14b) (VI.14r) (VI.15а) (VI. 156) , , г (VI.15B) ei°a °i eias Для большего приближения к действительным условиям, проис- ходящим на забое бурящейся скважины, А. А. Афанасьев в уста- новленные выше соотношения вводит величину Д*в, учи- тывающую повышение темпе- ратуры промывочной жидко- сти вследствие выделения в забойной зоне дополнитель- ного количества тепла Qfo6 в процессе разбуривания до- лотом породы: Qn об

A t.

Gc„

констант интегрирования 3 :#с — увеличением на эту разность значения Вг. Все остальные выкладки и расчетные соотношения остаются без изменения, но величина к при этом определяется не из выражения (VI.14r), а по формуле, име­ющей несколько иной вид: Ф-Ь ——- Л1В к*=————- ^£1——— (VI.17)

■ X ch

хн

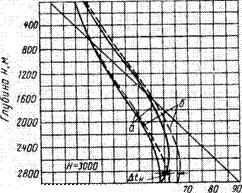
Как видно из кривых, построенных А. А. Афанасьевым, вели­чина приращения температуры оказывается тем больше, чем ближе рассматриваемое сечепие к забою (рис. 30).

ХН

ХН

^J-+%ch^- ‘f+— ai

ХН

ХН

аг sb а%—А.

-ch

=m^(^r+1)или т*=та*-Ь2’ д*=М^+0 или д»=^т±2′

W„ =

+

■ if.

(VI.16)

ю го зо w so во Температура tT,8,°c

Рпс. 30. Истинное распределение ратуры промывочной жидкости

темпе- __ вдоль ствола бурящейся скважины. Со — ара промывке; б — при бурении.

При этом величина Ata рассматривается как раз­ность забойпых температур потоков, обусловленная пе­редачей восходящему потоку тепла Qao6 в забойном сече­нии. Эта разность учиты­вается при установлении

ХН

Как следует из работы 16] того же автора, для практически ин­тересных случаев без ущерба для точности можно пренебречь влия­нием дроссельного эффекта, изменением координат центра тяжести и считать, что

shM^eh-^i-Л-,

21′ . Г 2Г 2аМв 2ах Ata

02-1-Х ‘ а1 А,— аг’ А, + ва 11 А —«г *

Приняв указанные допущения, можпо значительно упростить выведенные зависимости и рекомендовать для определения темпера­туры на забое следующие формулы:

2А,

0О -]- ГН, (VI. 18)

(‘о °о+ а ) „ у 2a1At„ 2Г

— т—— ехр—————————————————— —Я — —-гт—,

а2 ^ ^ а2 ТА ^ — а2

01 ^ ехр^я — 2<r=g^L4.eoH-/’tf. (VI.19)

Как видно из изложенного, аналитические зависимости громоздки для практического использования.

Более простые выражения могут быть получены на основе обра­ботки данных промысловых наблюдений за температурным режимом бурящихся скважин.

Комментарии запрещены.