Бурение грунтовых зондов, установка энергетических колодцев

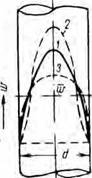
Известные из гидравлики закономерности движения жидкости относятся к изотермическому течению, когда температурные усло­вия,- при которых протекает процесс, остаются постоянными. Усло­вия движения в значительной мере усложняются, если температура жидкости меняется и создаются условия для теплообмена. При этом вследствие зависимости физико-механических свойств жидкости от температуры будет изменяться распределение скоростей по сече­нию, причем, как показывают наблюдения, это пзмепепие будет различным в зависимости от того, в какую сторону направлен тепло­вой поток. Это иллюстрируется эпюрой скоростей по сечению круг­лой трубы при неизотермическом течении ньютоновской жидкости (ламинарный режим), представленной на-рис. 20. Как видно из этого рисунка, профиль скорости получается более вытянутым в напра­влении оси при охлаждении и более сплюснутым при нагревании, если их сравнивать с обычным профилем, получающимся при изо­термическом течении.

Так как температура по длине трубы изменяется, то при неизо­термическом течении жидкости профиль скоростей, а также пара­метр Рейнольдса будут изменяться и вдоль трубы. Однако поскольку характер теплообмена в трубах определяется в основном скоростью и находится в зависимости от режима течения, то и коэф­фициент теплоотдачи по длине трубы будет изменяться. Следова­тельно, при точных расчетах теплоотдачи должны учитываться местные значения коэффициентов теплоотдачи. Получить местные зна­чения коэффициентов теплоотдачи довольно сложно, поэтому в прак­тических расчетах обычно пользуются формулами, которые дают возможность получать значения так называемых средних коэффи­циентов теплоотдачи.

Аналитические методы расчета теплоотдачи в условиях стабили­зированного ламинарного движения ньютоновских жидкостей в круглых трубах рассматривались Гретцем (1883), Нуссельтом (1910), а в дальнейшем Гребером, Левеком, Лейбензоном и др.

При этом основное дифференциальное уравнение теплопровод­ности, записываемое применительно к цилиндрическим координатам,

А’)

решалось с учетом следующих основных предпосылок. Физиче­ские копстанты сохраняются неизменными. На всем протяжении исследуемого участка абсолютно гладкой трубы устанавливается вполне развитое ламинарное течение жидкости, имеющей во всех точках одинаковую температуру. Температура на поверхности трубы остается постоянной. Перенос тепла в осевом направлении прене­брежимо мал по сравнению с переносом тепла по радиусу трубы.

Рис. 20. Распределение скоростей по сечению при пеизотермпчес. ком течении жидкости в трубе (ламинар­ный режим).

£

Учитывая упомянутые предположения, можно составить следу­ющее представление о характере теплообмена вдоль трубы в усло­виях ламинарного режима.

л
—
/
— <ul	11

0.3

О, г. 0.2 , » г 19ре’ О

Рис. 21. Критерий Нуссельта в функции длины трубы.

1 — изотермическое течение; 2 — охлаждение каиельны х жидкостей; S — нагревание ка­пельных жидкостей.

В месте входа жидкости в трубу, т. е. в начальном сечении, интенсивность

(ПЫ)

теплообмена бесконечно велика. Затем по мере удаления от этого сечения в направ­лении потока на небольшом отрезке трубы коэффициент теплоотдачи резко уменьшается, а затем медленно приближается к некоторому определенному постоянному значению (рис. 21). Наступает тепловая стабилизация потока, характеризу­ющаяся соблюдением условия

а = 3,65

которое чаще записывают в виде

Nu = 3,65, (Ш.2)

где Nu — параметр Нуссельта.

Длина участка, на протяжении которого происходит тепловая стабилизация потока (участок тепловой стабилизации или началь­ный термический участок) и с точностью до 1% устанавливается

40

Как видно из выражения (III.1), коэффициент теплоотдачи в условиях стабилизированного теплового потока при ламинарном режиме полностью определяется только теплопроводностью и диа­метром трубы и совершенно не зависит от скорости движения

предельное значение параметра Нуссельта (равное 3,65), может быть найдена из условия

где Ре — среднее значение параметра Пекле, представляющего собой безразмерпый комплекс:

ЖИДКОСТИ.

При пестабилизированпом тепловом режиме коэффициент тепло­отдачи и длина стабилизирующего участка существенно зависят от скорости потока.

Лайоп (27) решает ту же задачу, определяя коэффициент тепло­отдачи аналитически, несколько изменив условия. Он принимает, что постоянным является тепловой поток, а не температура. При такой постановке вопроса температура жидкости, как и температура стенки, оказывается линейной функцией расстояния. В результате такого решения получается зависимость

u^4,36-Ј — или Nuj =4,36,

из которой следует, что при стабилизированной теплоотдаче (а = const) критерий Нуссельта является величиной постоянной и равной 4,36.

В обоих вариантах решения значения Nu получены для пара­болического распределения скоростей, что может наблюдаться только при чрезвычайно малых температурных напорах или неиз­менных физических параметрах жидкости.

Однако в результате того, что физико-механические свойства жидкости зависят от температуры, распределение скоростей будет изменяться в зависимости от того, в какую сторону будет направлен тепловой поток. Это приводит к тому, что расхождение результатов, получаемых па основе аналитических формул, с опытными данными иногда может быть очень велико. Поэтому в настоящее время для практических расчетов предпочитают пользоваться так называемыми критериальными зависимостями, которые вытекают из основных положений теории подобия.

Хотя такого рода критериальные зависимости являются чисто эмпирическими, тем не менее они широко используются в практике расчетов, так как позволяют результаты отдельных опытов распространять на все подобные явления и тем самым намного облег­чают решение поставленной задачи.

Осноиными критериями, при помощи которых может быть опи­сан процесс конвективного теплообмена, являются критерии Фурье — Fo, Пекле — Ре, Нуссельта — Nu, Грасгофа — Gr, Рей­нольдса — Re, Прапдля — Рг. Первые три составляют группу критериев, описывающих чисто тепловые процессы; другие три критерия являются вспомогательными, так как вытекают из усло­вий механического подобия.

Рассмотрим указанные критерии более подробно.

Критерии Фурье

[(Ш. З)

увязывает между собой время т, необходимое для заданного измене­ния температуры, физические константы а и размеры тела I. Так как в этот параметр входит время, критерий Фурье характеризует псч’тациопарный режим.

Критерии Нуссельта был получен при рассмотрении процесса теплообмена между потоком и стенкой:

и характеризует интенсивность теплообмена на границе жидкость — стенка. Область применения этого критерия ограничивается усло­вием, что рассматриваемый процесс теплообмена осуществляется только теплопроводностью в ламинарном подслое у стенки.

Критерий Пекле представляет собой комплекс

характеризующий отношение конвективных и кондуктивных пото­ков тепла при конвективном теплообмене.

Критерий Рейнольдса, будучи безразмерным комплексом, пред­ставляет собой отношение сил вязкости к силам инерции:

v dy "wT

(HI.6)

Re = — v

где v — скорость потока; d — диаметр трубы; v и р — кинемати­ческая и динамическая вязкости.

Многочисленными исследованиями было установлено, что кри­терии Рейнольдса полностью определяет режим течения ньютонов­ских жидкостей: при значениях Re <Г 2300 паблюдается ламинар­ный режим движения, при Re $> 2300 начинается переход к турбулентному режиму.

Критерий Прапдля характеризует физические свойства жидкости и представляет собой комбинацию двух критериев — Пекле и Рей­нольдса:

Ro a

(Ill 7)

Таким образом, критерий Прандля дает соотношение между кинематическими и тепловыми свойствами жидкости.

Критерий Грасгофа Gr связывает подъемные силы в жидкости, вызываемые разностью температур, и силы вязкости:

(II 1.8)

где р — коэффициент объемного расширения; g — ускорение зем­ного притяжения в м/сека; At— разность температур между стен­кой и жидкостью в °С; I — характерный линейный размер поверх­ности теплообмена в м.

В выражения для некоторых параметров входит величина, представляющая собой определяющий размер, т. е. тот линейный размер, которым определяется развитие рассматриваемого про­цесса. В частности, при рассмотрении конвективного теплообмена в круглых трубах в качестве определяющего размера обычно бе­рется диаметр. Для каналов иной формы сечения надо брать экви­валентный диаметр, равный учетверенной площади поперечного сечения канала, деленной на смоченный периметр сечения. Напри­мер, для труб кольцевого сечения эквивалентный диаметр будет равен разности диаметров наружной и внутренней труб.

В то же время в состав почти всех критериев входят те или иные величины, характеризующие физические свойства жидкости. Но так как в процессе теплообмена температура жидкости меняется, то будут меняться и ее физические свойства. Следовательно, важно условиться о некоторой единой, определяющей температуре, по которой можно было бы рассчитывать все необходимые величины для всех критериев.

Обычно за такую определяющую температуру принимают ту, которая в расчетах задана или легко может быть определена. Влия­ние же резкого изменения значений физических параметров в по­граничном слое учитывается особым безразмерным параметром.

По предложению М. А. Михеева в качестве такого параметра принимается отношение значения критериев Прандля Рг, выбран­ных по температуре жидкости tK и температуре стенки tc, в степени

0,25, т. е. (Рг,/Ргс)°’м.

Средняя по длине трубы температура жидкости определяется по следующей формуле:

tx = ta±At,

где ta — температура стенки в рассматриваемом сечении; A t — сред­нее значение температурного напора.

Знак плюс берется при охлаждении жидкости, знак минус при ее нагревании.

4 Заказ 10*и.

При проведении точных расчетов в качестве А 2 принимают среднелогарифмический температурный напор, который определяется по формуле 127]

Af,= ***=?*" , (III.10)

1пТГ — Д f и

где Д tt и Д/„ — соответственно наибольший и наименьший темпе­ратурные напоры.

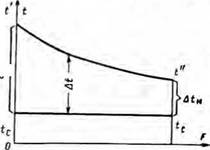
Согласно обозначениям на рис. 22 (изменение температурного напора A t вдоль трубы при постоянном значении коэффициента а и постоянной температуре стенки t0) имеем

А =

Рис. 22. Изменение темиературного напора вдоль трубы при <0 = const и а = const.

A t=r — L.

Как видно из представлен­ного рисунка, Д<6 и Atu соответ­ствуют температурным напорам на противоположных концах трубы.

Если превышение большего из температурных напоров над меньшим составляет до 70%, средний температурный лапор может быть определен как сред­неарифметический, т. е.

(III.11)

В этом случае, т. е. при условии, что AtjAtH *£ 1,7, разница между Д tt и Д£а пренебрежимо мала и составляет менее 4%. Когда же Ati/Atu^> 1,7, необходимо пользоваться только с редне логариф­мическим напором Д ts.

Выбирая в зависимости от указанных обстоятельств то или иное значение At и подставляя (III.10) или (III.11) в (III.9), можно определить среднюю температуру жидкости <ж.

Комментарии запрещены.