Бурение грунтовых зондов, установка энергетических колодцев

Если учесть, что толщина стенки бурильных труб 6 колеблется в пределах 8—11 мм, а X = 50 ккал/м • ч • 0С, то можно принять,

что у = 0,002 мг • ч • °С 1ккал и этой величиной можно пренебречь.

Тогда формула для определения коэффициента теплопередачи от кольцевого пространства к бурильным трубам значительно упро­стится и примет вид:

(V’5>

гдеах — коэффициент теплоотдачи от потока промывочной жидкости, движущегося в кольцевом пространстве, к стенкам бурильных труб;

— коэффициент теплоотдачи от стенки бурильной колонны к по­току, движущемуся внутри этой же колонны.

Определим величину к1, исходя из предположения, что промы­вочной жидкостью является морская вода и циркулирует она в сква­жине диаметром 0,27 м, в которой находятся 141 — мм бурильные трубы (da = 0,14 м, dv = 0,12 м). Расход промывочной жидкости Q примем равным 20 л/сек.

Режим течения воды в трубах и в кольцевом пространстве опре­делим по известным формулам гидравлики.

Зная значения D, dt и da, найдем скорости потока в бурильной колонне и в кольцевом пространстве: vt = 1,77 м/сек, у, „ —

= 0,476 м/сек.

Допустим, что средняя температура воды £ср в условиях бурения может изменяться от 10 до 150° С. Примем наихудшие для расчета условия, т. е. будем считать, что tev = 10° С и соответствующие ей значения v — 1,32 • 10"® м21ч. Тогда критерии Рейнольдса для бурильных труб и кольцевого пространства будут равны Rer = = 16,2 • 10®; Re, n = 4,72 • 10*.

Таким образом, в данных условиях в трубах и в кольцевом про­странстве наблюдается турбулентный режим движения. Исходя из. этого, величины ocj и р х будем определять из критериальных зависи­мостей (III.4) и (III.13), которые в результате несложных преобра­зований и подстановки численных значений входящих в них величин были приведены к виду (43):

TOC o "1-5" h z рг = 0,Ш. Рг<м(М2*)в‘ (Vfi)

otj = 0,238Х Рг0-* ^ ,2^!L!®§. у’* (V.7)

при Re = 1 ■ 10* — г 5 • 10® и Рг = 0,6 2500.

Эти величины были вычислены по формулам (V.6) и (V.7) для

воды в иитервале температур от 10 до 150° С с использованием фи­

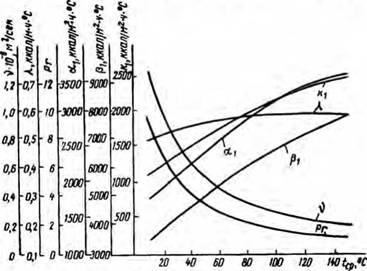
зических параметров, приведенных в работе С. Н. Шорина. Далее по формуле (V.5) вычисляли коэффициент теплопередачи /с, для каждого конкретного температурного интервала. Результаты рас­четов представлены в табл. 22 и на рис. 26.

Кривые показывают, что коэффициент теплопередачи кг для воды с увеличением средней температуры в скважине также увеличи­вается, а так как температура растет с увеличением глубины сква­жины, то величина кх находится в прямой зависимости от глубины.

Определим величину коэффициента к1 на примере, взятом из нефтепромысловой практики.

В работе (76) приводятся данные по замеру температуры цирку­лирующей промывочной жидкости (воды) в трех скважинах на пло­щади Озек-Суат. Жидкость прокачивали через компрессорные трубы. Конструкции скважин приведены в табл. 23. После установившегося теплового режима промывки были получены данные по замеру тем­ператур, приведенные в табл. 24.

Так как по данным замеров в скв. 9 при расходах 7 и 10 л! сек в трубах и за трубами наблюдался турбулентный режим, то коэффи­циент теплопередачи А, рассчитывали по формулам (V.5) и (III. 13).

При этом получили следующие величины: при расходе 7 л/сек к1 — 2724 ккал1мг ■ ч • °С, а при расходе 10 л1сек кх — = 3621 ккал1м2 • ч • °С.

Так как диаметры труб и средняя температура в скважинах были в обоих случаях одинаковы, то можно сделать вывод, что уве­личение коэффициента теплопередачи объясняется повышением рас­хода жидкости.

Большой интерес представляет вопрос о порядке величины коэф­фициента теплопередачи /с1 при прокачке в скважину глинистого

раствора. Приближенно этот вопрос можно решить следующим образом.

Определим режим течения глинистого раствора, для чего вос­пользуемся формулами (III.23), (III.23а).

Из расчетов для воды известно, что при Q = 20 л/сек vx = = 1,77 м/сек, vK п = 0,476 м/сек, dt — 0,12 м, dB = 0,14 м, D — = 0,27 м.

Допустим, что удельный вес глинистого раствора, циркулиру­ющего в скважине, равен 1,5 Г/см3. Тогда остальные параметры этого раствора ориентировочно могут быть приняты равными: т0 = 103 дин/см2, т) = 0,24 пз.

Подставляя известные величины в зависимости (II 1.23) и (II 1.23а), имеем Rei — 2200, Rei „ = 183.

Следовательно, можно принять, что при заданпьгх условиях в трубах и в кольцевом пространстве наблюдается структурный режим потока. В работе [60] приводятся следующие значения пара­метра Нуссельта при структурном движении глинистых растворов: в круглой трубе Nui = 4,47, а в кольцевом пространстве Nu|,„ = = 4,38.

а‘> = Ки»7Г^’ <V’8>

(Jlp = Nu;-^, (V.9)

ul

где aj и P, p — коэффициенты теплоотдачи от раствора, движу­щегося в кольцевом пространстве и в трубах к стенкам их.

Полный коэффициент теплопередачи к1 при движении глинистого раствора найдем из зависимости (V.5), заменяя велпчипы их значе­ниями из выражений (V.8) и (Y.9).

j, °1рР|р К Nll«n____________________________

Подставляя численные значения величин, входящих в формулу

(V.10), получим значение к[ — 9,2 ккал/м2 • ч • “С. Таким обра­

зом, коэффициент теплопередачи к[ при движении в скважине гли­нистого раствора значительно меньше, чем при прокачивании воды с тем же расходом.

Комментарии запрещены.